装配生产中机械加工尺寸偏差源敏感度检测方法

2020-10-13史召峰

辽东学院学报(自然科学版) 2020年3期

史召峰

(安徽工业经济职业技术学院机械与汽车工程学院，合肥 230051)

装配生产不仅是经济建设的核心组成成分，还是一个国家的综合国力具体体现，没有发达的装配生产技术，就不能实现工、农、国防和科学技术的现代化，第三产业的发展也将后继乏力。装配生产又称作国家工业化建设的原动机[1]。

偏差是由尺寸细微变化造成的与名义值间出现的偏离值。产品的偏差源通常分为机械加工尺寸偏差、机械加工产品形状偏差和机械加工位置偏差三种类型。装配生产中机械加工尺寸偏差通常指零件在机械加工时受到各种偏差源的影响，最终生成的实际机械加工零件尺寸与理论尺寸的偏离值。由于机械加工零件尺寸偏差直接影响零件的质量、生产情况以及市场响应时间，所以尺寸偏差控制是学术与工业2个领域的重点研究问题，然而在零件装配生产中机械加工复杂性会造成零件尺寸偏差，对机械加工零件尺寸生产和零件加工质量产生负面影响，尺寸偏差还会造成产品的反复调整，无限延长零件的投产期[2]。

机械加工零件尺寸偏差会影响产品美观及使用性能[3]，也令产品在使用时更易发生故障。如何准确、快速地检测出装配生产中机械加工尺寸偏差源敏感度成为了当前工业领域亟待解决的问题之一。为了解决这些问题，众工业领域专家提出了基于多维矢量环的机械加工尺寸偏差源敏感度检测方法。

1 装配生产中机械加工尺寸偏差源敏感度检测

以内襟翼摇臂装配零件为例，进行机械加工尺寸偏差源敏感度检测。其中，内襟翼摇臂装配及内襟翼摇臂剖面如图1、图2所示。

如图2所示的内襟翼摇臂主要包含P翼身、P摇臂、P前接头、P后接头和P销等5个零部件，该装配体的偏差源用a1、a2、a3、…、a13表示。

根据上述分析，设计机械加工尺寸偏差源敏感度检测流程，具体流程如图3所示。

1.1 机械零件尺寸偏差模型的构建

假设n为与质量控制有关的机械加工零件表面尺寸特征数量，说明第k工位第i个表面的零件尺寸特征包括方向、定位和尺寸3个向量[4]，它们分别为ni=[nix,niy,niz]T、pi=[pix,piy,piz]T和Di=[di1,di2,…，dim]T，其中m表示机械加工尺寸向量Di的维度。Di中元素是机械加工零件的几何尺寸和公差信息。

第k工位第i个表面的机械加工零件尺寸特征能够表现成如下形式：

(1)

n个表面的机械加工零件尺寸特征如下：

(2)

零件在进行机械加工时，会因为其受到的偏差源影响，造成实际得到的尺寸特征与理想设计的机械加工零件尺寸特征出现偏离，生成尺寸偏差[5-6]。利用式(1)获取第i个表面的机械加工零件尺寸偏差：

(3)

式(3)中：

△ni=[△nix,△niy,△niz]T

(4)

△pi=[△pix,△piy,△piz]T

(5)

△Di=[△di1,△di2,…，△din]T

(6)

通过式(1)～(6)，完成对单个机械加工零件尺寸偏差模型的构建。假设X(k)是第k个工位在进行实际机械加工后得到的零件尺寸特征，X0(k)是第k个工位理想的零件尺寸特征[7]。则机械加工零件尺寸偏差x(k)的计算公式如式(7)所示。

x(k)=X(k)-X0(k)=

(7)

以圆锥形的机械加工零件为例，这种圆锥形零件模型如图4所示。

1.2 获取机械加工尺寸偏差相关信息

机械加工尺寸公差通常指机械加工产品尺寸所允许的变动量。在基本尺寸相同时，如果机械加工产品的尺寸公差越小，那么其精度就越高。

机械加工尺寸公差计算公式为：

|S|=bestmax-bestmin

(8)

其中，bestmax和bestmin分别表示机械加工产品允许的最大和最小两种极限尺寸。

国际上将机械加工产品尺寸的标准公差划分为18个等级，这18个等级分别为IT1、IT2、IT3、…、IT17和IT18。机械加工零件的公差数值越小、精度越高，机械加工尺寸精度越高，产品的制造工艺越复杂，成本越高。

1.3 机械加工零件尺寸偏差源敏感度检测

假设机械加工尺寸为{a1,a2,…,an}，装配尺寸{U1,U2,…，Um′}被包含于装配体中，多维矢量闭环可以表现成如下形式：

hD′=D′(a1,a2,…,an′,U1,U2,…,Um′)

(9)

式(9)中，D′是机械加工零件在空间中的矢量方向[8]，D′=(u,v,w,α，β，γ)和D′={x′,y′,θ}分别表示3维和2维空间，u、v、w、x′和y′是机械零件的矢量位置参数。α、β、γ、θ是机械零件的矢量方向参数。

矢量环由开环与闭环组成。开环用于说明机械零件尺寸对零件特征间距离的影响。闭环用于说明机械零件间的尺寸关系[9]，多维矢量开环表现形式如下：

(10)

通过多维矢量环创建其标量方程组，从式(11)能够看出，只有计算出a和U的显性表达式才能得到装配生产中机械加工尺寸偏差源的敏感度，由于式(9)和式(10)仅隐性说明了各机械加工零件尺寸间的关系，则采用数学方法处理。

(11)

装配偏差体现了机械加工尺寸的细微改变，采用泰勒级数能够将多维矢量的开环与闭环线性化[10]，利用矩阵求逆，完成对机械零件偏差关系的显性表示。

式(9)与式(10)采用泰勒级数展开后得：

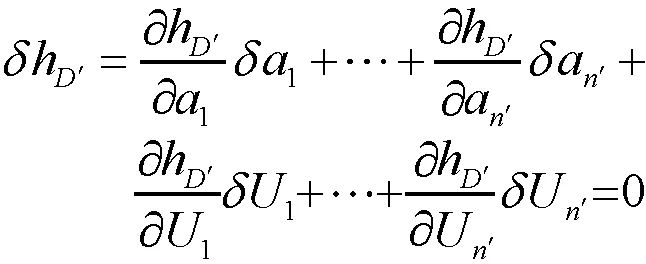
(12)

(13)

其中，δa是尺寸的a细微变化。

利用矢量环线性表达式能够解决机械加工尺寸偏差源的敏感度问题[11]。

矩阵形式的机械加工零件尺寸矢量闭环与开环的标量方程分别为：

Aδa+BδU=0

(14)

δG=Cδa+EδU

(15)

式(14)与式(15)中，A与B表示矢量闭环标量函数，关于机械加工与装配两种尺寸改变情况的偏导数矩阵；C与E表示矢量开环标量函数对机械加工与装配两种尺寸改变情况的偏导数矩阵；G表示间距尺寸细微改变的矢量矩阵；a与U分别表示机械加工与装配2种尺寸对应的细微改变情况的矢量矩阵。

对式(14)与式(15)做变换操作[12]，得：

δU=-B-1Aδa

(16)

δG=(C-EB-1A)δa

(17)

通过式(11)可以看出式(16)和式(17)中-B-1A是装配生产中机械加工尺寸对偏差源改变情况的敏感度矩阵，C-EB-1A是开环距离对偏差源改变情况的敏感度矩阵。

通过上述的敏感度矩阵即可实现对机械加工零件尺寸偏差源敏感度的检测。

2 检测性能测试

2.1 实验环境

在装配生产中机械加工尺寸出现偏差问题，普遍由工程师的工作经验逐一检查各装配工位的偏差源因素状态。因为装配生产中机械加工零件由多工位制造，所以工程师会按照其工作经验判断当前偏差问题出现的位置，在工程师判断的位置内查找具体的偏差来源，这种检测方法检测效率低。为了解决这个问题提出基于多维矢量环的机械加工尺寸偏差源敏感度检测方法，该方法是在观测机械加工零件装配状态下进行推理，根据推理结果得出不同的偏差源故障可能性。

为了验证所提的基于多维矢量环的机械加工尺寸偏差源敏感度检测方法的有效性，对所提方法进行了性能测试，实验平台由三台处理器为8核，内存为64G的计算机组成。实验数据为蒙特卡洛生成的实验样本集，样本中每一个样本均包含全部偏差源和观测两种节点的状态信息，在实验中将一部分的观测节点状态信息设定成已知，另一部分的观测节点状态信息被设定成未知，通过这种方式模拟机械加工尺寸偏差源敏感度检测证据变量。其中，实验样本集如表1所示。

表1 实验样本集

2.2 性能测试与结果分析

图5是不同数量的观测节点下，基于多维矢量环的机械加工尺寸偏差源敏感度检测方法的检测效果曲线。

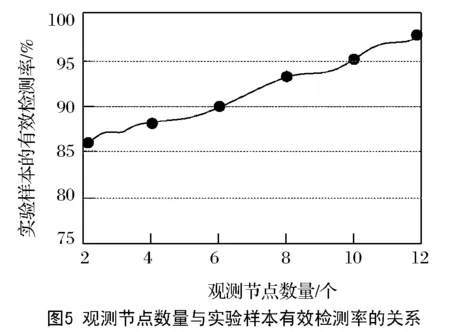
由图5可以看出，随着测点状态值数量的增多，实验样本的有效检测率也随之增高。在全部测点偏差状态值均被观测的前提下，所提方法对实验样本的有效检测率达到97%以上。在观测到部分测点偏差状态值的情况下，所提方法仍能对大部分的实验样本进行有效识别。

噪声是影响机械加工零件尺寸偏差源敏感度检测结果的另一项因素，噪声通常来源于假设条件、测点数据样本大小、数据随机性等。因为在所提方法中这些噪声因素体现在节点条件概率的准确性上，所以利用对条件概率施加噪声的方式模拟噪声对检测结果的影响，通过上述实验数据可知，观测节点数量越多，所提方法对实验样本的有效检测率越高。

图6是不同噪声水平下，基于多维矢量环机械加工尺寸偏差源敏感度检测方法的检测效果曲线。

从图6可以看出，噪声等级越高，所提方法对实验样本的有效检测率越低。分别在偏差源和检测两种节点上施加噪声，对比施加噪声后的有效检测率曲线。由此可知，随着噪声的加大，实验样本的有效检测率逐渐降低，噪声对偏差源节点的影响关系较大。噪声较小情况下，有效检测率曲线表现比较平缓，在噪声等级小于0.5时，所提方法对实验样本的有效检测率仍高于90%，这说明在施加噪声的节点类型存在差异后，所提方法仍能对大部分的实验样本进行有效检测。

机械加工尺寸偏差源敏感度检测精度对比如表2所示。