冲击载荷作用下矩形风窗动态分布特征与破坏机理

2020-10-13何子建沙芳菲董新慧

煤炭学报 2020年9期

李峰,何子建,张悦,沙芳菲,董新慧,刘尧

(1.中国矿业大学(北京) 深部岩土力学与地下工程国家重点实验室，北京 100083; 2.中国矿业大学(北京) 应急管理与安全工程学院，北京 100083; 3.中海油研究总院，北京 100028; 4.中国中材国际工程股份有限公司,北京 100102)

煤炭资源是我国的主要能源，煤矿事故灾害是制约煤矿安全生产的关键因素。大多数矿井属于高瓦斯和煤与瓦斯突出矿井，一半以上的矿井具有瓦斯(煤尘)爆炸危险性。在我国煤矿的灾害事故中，瓦斯、煤尘爆炸事故造成的伤亡人数占总伤亡人数的60%以上。瓦斯(煤尘)爆炸中矿井通风构筑物损毁严重，致使通风系统遭到严重破坏而发生紊乱，导致灾情迅速扩大波及井下其他区域，致使此类事故应急处置与救援难度相当大[1-2]。如果能保证关键的通风构筑物在事故发生时不被破坏，整个通风系统依然可靠，实现通风系统在灾变条件下的有效性、那么就可以为应急处置与救援提供可能条件，就可以尽可能减少瓦斯(煤尘)爆炸事故造成的破坏。目前，国内外学者在瓦斯爆炸冲击波传播规律、衰减规律、冲击波破坏作用等方面进行了理论与实验研究[3-7]。周杰[8]采用平面冲击波方法，计算了泡沫材料有限元模型前部、内部及后部监控点的压力波曲线，了解冲击波与材料作用的反射、透射的特征。爆炸冲击波传播过程中在固定构筑物处会出现多个波峰震荡，在此种区域有着显著的超压与振荡现象，对矿井通风设施破坏效应明显，但固定构筑物(如风门、风窗、密闭等)在爆炸冲击波作用过程中具体的破坏原因、过程和机理尚不清楚。

笔者研究瓦斯爆炸冲击载荷作用下矩形风窗动态响应特性与破坏机理，对保护风窗在瓦斯(煤尘)爆炸事故中不被破坏，实现通风系统在灾变时期的有效性，为应急处置与救援提供可能性，减少人员伤亡和损失具有重要的理论指导意义与实际价值。

1 矩形风窗动态响应计算模型

1.1 矩形风窗振动控制方程

矿井矩形风窗的尺寸大都符合薄板的尺寸要求(厚度与板面宽度的比值在1/5～1/80)，薄板模型可以抗弯、抗扭，也可以承担平面内的应力，符合矩形风窗的力学分析要求，以中性面建立坐标系，如图1所示。以薄板模型研究矩形风窗在爆炸冲击载荷作用下的动态响应特征与破坏机理。

图1 矩形风窗的坐标系

在冲击载荷q(x,y,t)作用下，根据瞬态平衡条件，得矩形风窗受迫振动的微分方程[9]:

(1)

其中，w(x,y,t)为挠度;D为风窗的弯曲刚度;ρ为密度;t为时间。先求解式(1)的齐次方程，当q(x,y,t)=0时，矩形风窗自由振动微分方程[10]为

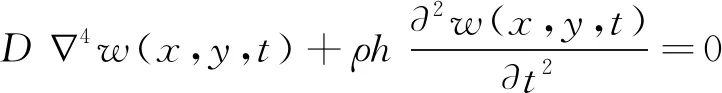
(2)

假设矩形风窗的振动具有如下随时间的谐振子变化规律[10]:

w(x,y,t)=W(x,y)eiωt

(3)

其中，ω为自振频率;W(x,y)为矩形风窗的挠度振型函数。把式(3)代入式(2)，变换得

(4)

其中，k4=ρhω2/D。由矩形风窗的受力分析可得各物理量之间的关系为

若用W(x,y)表示各物理量，关系式为

(11)

(12)

式中，Mx，My为x,y方向的弯矩;Mxy为扭矩；Qx，Qy为x,y方向的横向剪力;Vx，Vy为x,y方向的横向总剪力;ν为泊松比。

1.2 矩形风窗振动Hamilton体系对偶方程

为了解耦控制方程中的物理量，需引进Hamilton体系对偶方程[11-12]。由式(7)与式(12)可得

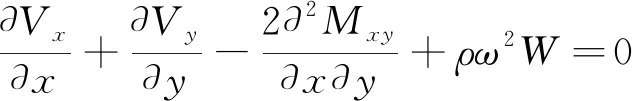
(13)

(14)

由(10)得

(15)

综合上述可得

(16)

联合式(5)，(12),(15)得

(17)

令向量v=[W,θ,-Vx,Mx]，可得Hamilton体系对偶方程:

v′=Hv

(18)

即

1.3 Hamilton体系对偶方程的求解

按照辛几何方法[11]，利用分离变量法求解方程(18)，令

v=Y(y)X(x)

(19)

方程(18)有如下形式的解:

V(x)=ξ(x)ψ

(20)

将式(20)代入方程(18)中，得

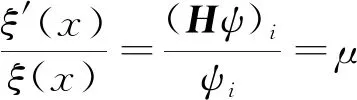
(21)

因此

(22)

由此可得:μ与-μ均是哈密顿矩阵H的特征值，则方程(18)解的形式为

v=(a1eμx+b1e-μx)Y(y)

由此可得挠度振型函数W(x,y)为

W=(a1eμx+b1e-μx)W(y)

(23)

将(23)代入(2)得

(24)

方程(24)有如下形式解:W(y)=eλy，代入式(24)可得

(λ2+μ2)2=k4

(25)

因此，可得

λ12=±iα1，λ34=±α2

(26)

同理可得

μ12=±iβ1，μ34=±β2

(27)

由式(26)与(27)可得

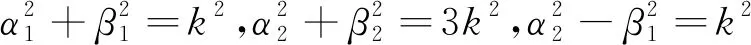
(28)

由此可知:沿x,y方向的挠度振型分别为W(x)，W(y)，具体形式[13-15]可写为

W(x)=a1eiβ1x+b1e-iβ1x+c1eβ2x+d1e-β2x=

A1cosβ1x+B1sinβ1x+C1coshβ2x+D1sinhβ2x

(29)

W(y)=a2eiα1y+b2e-iα1y+c2eα2y+d2e-α2y=

A2cosα1y+B2sinα1y+C2coshα2y+D2sinhα2y

(30)

2 矩形风窗振动的挠度振型函数

设矩形风窗的尺寸为a×b，弹性模量为E。基于井下矩形风窗的安装特点，取风窗四边为固支边界(C-C-C-C)。沿y方向有:W(x,0)=0，∂W(x,0)/∂y=0;W(x,b)=0，∂W(x,b)/∂y=0。

由式(30)可得

上式有解，则左侧系数矩阵行列式为0，得出沿y方向的频率方程为

(31)

令C2=1，联合频率方程解得

A2=-1，B2=k1α1/α2，C2=1，D2=-k1

因此

coshα2y-k1sinhα2y

同理

coshβ2x-k2sinhβ2x

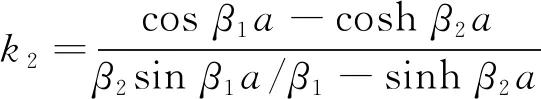
因此方程(2)矩形风窗振动的挠度振型函数为

W(x,y)=C1C2W(x)W(y)=C1×C2×

(32)

3 矩形风窗振动的动态响应特征

3.1 控制方程求解

非齐次方程(1)解的形式可写成

(33)

将式(33)代入式(1)中可得

q(x,y,t)

由于

因此

两边同时乘以Wm(x,y)，根据挠度振型函数的正交性[16]可得

并在整个平面区域上积分，得

(34)

因此

根据杜哈梅积分可得

假设爆炸冲击载荷作用在矩形风窗上的压力可看作瞬时均布载荷，具有如下形式:

q(x,y,t)=q0δ(t-t1)

因此

由此可得冲击载荷作用下矩形风窗振动控制方程(1)的解为

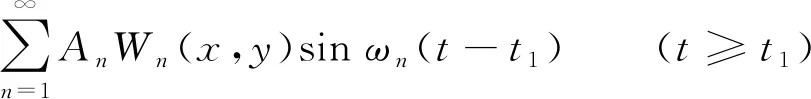
(35)

3.2 矩形风窗动态响应特征

3.2.1矩形风窗振动参数

取钢制矩形风窗的参数为:h=0.06 m，ρ=2 800 kg/m3，E=72 GPa，ν=0.3，a×b=3 m×3.6 m。联立式(28),(31)，运用牛顿迭代法求解四边固支条件下(C-C-C-C)矩形风窗的主振型函数，其前10阶振动参数计算值见表1。

表1 四边固支(C-C-C-C)矩形风窗主振型函数前10阶振动参数

3.2.2主振型挠度的动态分布特性

由式(34)与式(35)计算可得:冲击载荷下四边固支(C-C-C-C)矩形风窗前10阶振动参数值，见表2。由表2可得:1阶、5阶、6阶振动函数为主振型函数，其振动的固有频率分别为308，975，1 309 Hz;系数(An/q0)比较可得:5阶系数约为1阶系数的9.4%，6阶系数约为1阶系数的4.9%，因此取前10阶主振型完全满足分析要求。3种主振型的挠度分布，如图2所示,图2中Am为常数系数，矩形风窗挠度的主要分布范围分别为风窗中心区域、两条短边附近与两条长边附近区域。

表2 冲击载荷下四边固支(C-C-C-C)矩形风窗前10阶振动参数值

图2 主振型挠度动态分布

图3 主振型应力动态分布

图4 主振型的最大主应力与应变

3.2.3应力与应变动态分布特性

(1)应力、应变动态分布。1阶、5阶、6阶振动函数为主振型，其应力动态分布如图3所示,图3中An为常数系数。1阶主振型x方向、y方向与xy扭应力集中区域分别为:长边中点区域与风窗中心区域、短边中点区域与风窗中心区域、矩形边角附近区域;5阶主振型x方向、y方向与xy扭应力集中区域分别为:四边中点及其附近区域与风窗四角附近区域、短边中点及其附近区域、矩形边角附近区域与其中一条长边中点附近区域;6阶主振型x方向、y方向与xy扭应力集中区域分别为:短边中点及其附近区域、四边中点及其附近区域与风窗四角附近区域、矩形风窗边角附近区域与一条短边中点附近区域;1阶、5阶、6阶主振型的x方向、y方向应力在矩形风窗中心区域均存在较明显的应力集中现象。

由此可得:应力集中的区域主要有:① 四边中点及其附近区域;② 矩形风窗中心区域;③ 矩形风窗四角附近区域。由于应变、弯矩动态分布与应力动态分布相似，因此可根据应力集中区域推断出矩形风窗的主要破坏区域。

(2)最大主应力与应变动态分布。1阶、5阶、6阶主振型最大主应力与应变动态分布如图4所示。由图4可知:1阶主振型最大主应力与应变集中区域分别为:四边中点区域与矩形风窗的中心区域、矩形风窗中心区域;5阶主振型最大主应力与应变集中区域分别为:四边中点及其附近区域、长边中点区域与短边中点附近区域;6阶主振型最大主应力与应变集中区域分别为:四边中点及其附近区域、短边中点区域与长边中点附近区域;1阶、5阶、6阶主振型的最大应力与应变在矩形风窗中心区域也均存在较明显的应力集中现象。

由此可得:最大主应力、最大主应变主要集中区域为矩形风窗四边中点及其附近区域与矩形风窗的中心区域。最大主应力/应变为第一主应力/应变，其集中区域与应力、应变、弯矩的集中区域保持一致，也可由此推断出矩形风窗的主要破坏区域。

3.2.4横向总剪力动态分布特性

沿矩形风窗厚度方向的剪力与弯矩产生的剪力之和为横向总剪力，其分布如图5所示，结合图3(a)与图4(a)可知:横向总剪力值与主应力值相比较小(大约相差两个数量级)，对矩形风窗动态破坏的影响作用相对较小，分析时可以忽略。

图5 1阶主振型横向总剪力

图6 主振型最大剪应力

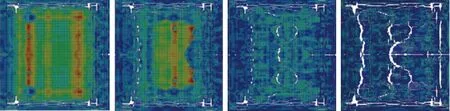
图7 四边固支矩形风窗(C-C-C-C)动态破坏过程

3.2.5矩形风窗动态破坏过程

基于第三强度准则，矩形风窗中最大剪应力动态分布如图6所示，由图6可知:1阶主振型的最大剪应力主要分布在四边中点区域与矩形中心区域;5阶主振型的最大剪应力主要分布在两条短边中点区域与沿矩形长轴中心区域;6阶主振型最大剪应力主要分布在两条长边中点区域与沿矩形短轴中心区域。由此分析可得破坏过程如下:冲击载荷作用下四边固支(C-C-C-C)矩形风窗发生损伤破坏的位置位于四边中点区域与矩形风窗中心区域，主要沿着风窗长轴的中心区域破坏，其次是沿着短轴的中心区域破坏。

4 矩形风窗动态破坏过程模拟

基于LS-DYNA软件，采用PLASTIC_ KINEMATIC材料模型[17]，模拟分析矩形风窗在冲击载荷作用下的动态破坏过程，如图7所示，四边固支矩形风窗(C-C-C-C)动态破坏过程如下:首先风窗短边中心出现裂纹发生损伤破坏、风窗长边中心发生损伤破坏，然后是风窗中心区域发生破坏，破坏方向主要沿着长轴中心方向发展，其次会沿着短轴中心方向发展。最终主要的破坏区域为风窗的四周、中心区域、沿长轴与短轴中心区域;数值模拟分析的结果与理论分析结果完全吻合。

5 矩形风窗动态破坏机理探讨

冲击载荷作用下四边固支(C-C-C-C)矩形风窗振动以1阶为主(主频)，5阶与6阶次之。应力、应变、弯矩动态分布相似，由图2～4可知:3个主振型的主要集中区域有:四边中点及其附近区域、矩形风窗中心区域、矩形风窗四角附近区域。由图8可得:最大主应力与主应变主要集中区域为矩形风窗四边中点及其附近区域、矩形风窗的中心区域。由图6(a)可得:1阶主振型四边中点区域最大剪应力明显大于中心区域的最大剪应力，因此首先发生破坏的位置应是四边中点区域，其次是矩形风窗的中心区域;由图6(b)可知，除了四边中点区域的最大剪应力集中以外，5阶主振型沿矩形长轴中心区域也具有最大剪应力集中现象，因此，破坏的位置应是沿着长轴中心区域扩展;同时由图6(c)可知:6阶主振型沿矩形短轴中心区域也具有最大剪应力集中现象，因此破坏的位置沿着短轴中心区域也会有相对小范围的扩展。

结合图7综合分析可知:由1阶主振型(主频)动态分布特征可以推断出矩形风窗的起始破坏位置为矩形四边中心区域，由5阶、6阶主振型可以判断破坏的发展方向与趋势为沿着长轴或短轴中心区域扩展，3个主振型综合构成了冲击载荷下四边固支(C-C-C-C)矩形风窗振动的主振型函数。