运用相似法破解一类勾股题

朱小扣

(安徽省无为第三中学城北校区 238300)

本文将从勾股定理的相似证法得到启发，通过相似的性质可以解决勾股定理这一章节的很多题目.希望本文能对同学们有所启发.

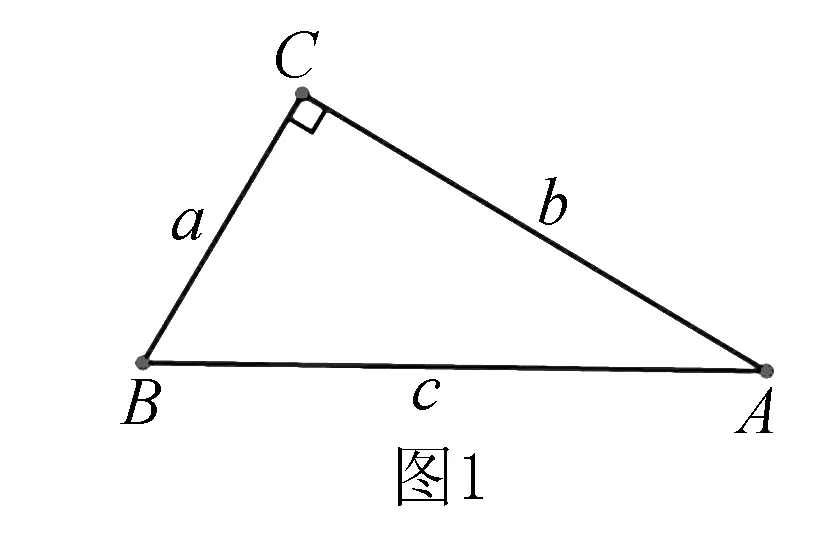
例1 如图1，在Rt△ABC中，∠C=90°，a,b,c分别是∠A,∠B,∠C所对的边.

求证：a2+b2=c2.

例1是勾股定理的证明,事实上，勾股定理是一个基本的几何定理，指直角三角形的两条直角边的平方和等于斜边的平方.其证明方法有很多，在人教版八年级教材下册第23页(文[1])，是用赵爽的勾股弦图证明的.后来,教材又在第30页的阅读材料中，又提供了毕达哥拉斯证法与美国总统加菲尔德的证法.考虑到这个等式左右都是二次的，故不能用线段长度(一次的)来证明之，首选应该采用面积(二次的)来证明.根据数学证明的原则，可以采用相似法、托勒密定理等来证明，但不能用正弦定理、余弦地理来证明，因为这犯了循环论证的错误，即不能用相互联系的后来高级的知识证明开始初级的知识.

笔者查阅很多资料发现文[2]中的证法很实用：

证明如图2.作CD⊥AB于点D,易证△CBD∽△ACD∽△ABC.

由面积比等于相似比的平方可得：S△CBD∶S△ACD∶S△ABC=a2∶b2∶c2

可设：S△CBD=ka2,S△ACD=kb2,S△ABC=kc2(k>0),结合S△CBD+S△ACD=S△ABC得：

ka2+kb2=kc2，故a2+b2=c2，即证.

上述解法利用相似的性质，简单而直观的证明出勾股定理，这种新的思想应该推广.又如：

例2如图3，过直角三角形的三边向外作等边三角形，求证：S1+S2=S3

证明易证3个等边三角形相似，由面积比等于相似比的平方可得：S1:S2:S3=a2:b2:c2可设：S1=ka2,S2=kb2,S3=kc2(k>0),结合勾股定理a2+b2=c2得：S1+S2=k(a2+b2)=kc2=S3，即证.

同样的(如图4，图5)：

同理可证：过直角三角形的三边向外作等边正多边形，都有：S1+S2=S3

同样的如果不用相似法，很难用计算面积来解决下面的题目.

例4如图6，在四边形ABCD中，AB∥CD,∠ADC+∠BCD=90°,以AD,AB,BC为边向外分别作等边三角形，其面积分别是S1,S2,S3,且CD=3AB,S1+S3=kS2,求k的值.

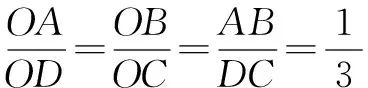
进而AD=2OA=2b,BC=2OB=2a，由三个等边三角形相似可得：

S1∶S2∶S3=(2b)2∶c2∶(2a)2.

由a2+b2=c2.

得：S1+S3=4S2,

故k=4.

用相似法还可以解决如下类似的题目：

例4如图7，四边形ABCD中，AD∥BC,∠ABC+∠BCD=90°,以AB,BC,CD为边向外分别作正方形，其面积分别是S1,S2,S3,且BC=2AD,S1=3,S3=9求S2的值.

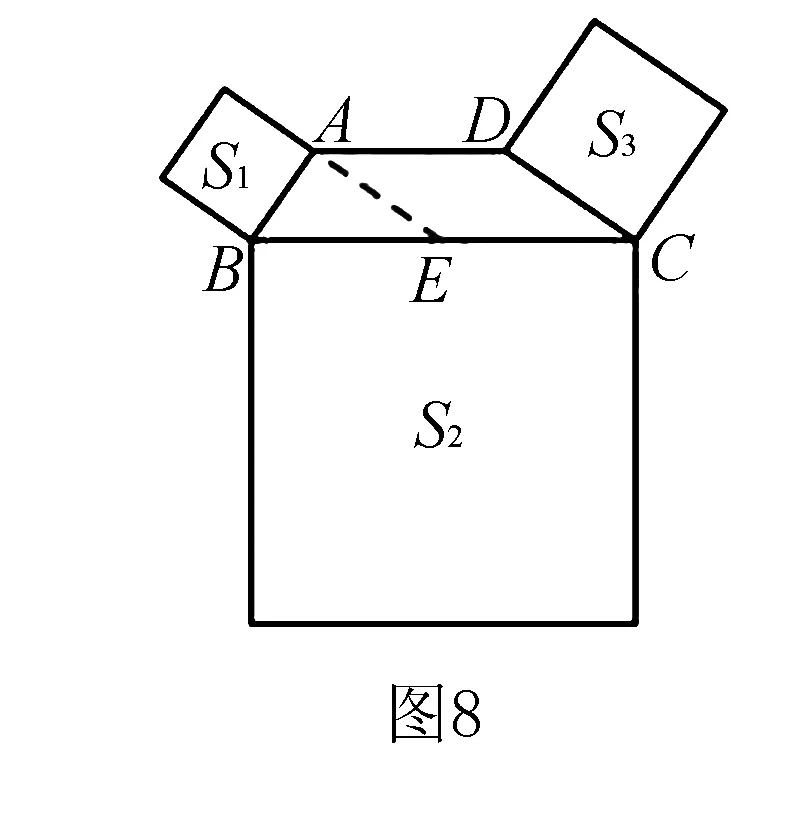
解过A作AE∥CD交BC于点E,则∠BAE=90°，易证AECD是平行四边形,则BC=2AD=2BE,AB2+AE2=BE2,如图8.

由三个正方形相似，得：

S1∶S2∶S3

=(AB)2∶(2BE)2∶(AE)2.

⟹S2=4×(3+9)=48.

[追踪训练]

例5如图9，已知在Rt△ABC中，∠ACB=90°，AB=4，分别以AC，BC为直径作半圆，面积分别记为S1，S2，则S1+S2=____.

答案:2π(过程略).

上面涉及到勾股数的题目，都可以用相似来解决.然而在很多版本的八年级数学教材都将相似放在了勾股定理之后，这很容易让学生忽视相似这种巧妙方法在勾股定理这一章节的应用，在此也希望专家在编写教材时，能把用相似证明勾股定理的这种方法写进教材.