基于航海雷达图像阴影反演波高算法研究
2020-10-13杨江洪顾宗山卢志忠
杨江洪 顾宗山 卢志忠
(1.中国电子科技集团公司第三十八研究所 合肥 230088;2.哈尔滨工程大学 哈尔滨 150001)
0 引言
海浪是海洋动力环境的重要因素,波高是衡量海水运动及海浪能量一个重要参量。实时提供精确的海浪监测信息有助于人们的海洋作业安全,因此海浪监测具有十分重要的科研意义和实用价值[1]。当前海浪监测方式有:人工观测,依赖于观测者经验积累,准确性较差;浮标、流速压力传感器能直接获得海浪参数,测量精度高,但观测范围较小;声学传感器测量距离远,然而自身噪声较高,难以获得高精度参数。以上的测量方法虽然可以直接获得海浪参数,但面临着精度不够高、花费较大,观测面小等问题。伴随着雷达技术技术飞速发展,雷达遥感装备观测海浪成为当前海洋测量技术的发展趋势。利用导航雷达对海况进行实时监测兼顾导航和测浪的功能,最大化提升导航雷达用途。
目前,遥感雷达图像反演海浪波高有两种方法,分别是海浪谱反演法和阴影图像反演法。海浪谱反演法是利用傅里叶变换获得雷达图像波数能量谱,计算信噪比,通过信噪比的平方根成线性关系来估测有效波高[2-5]。而海浪谱反演法难度较大,图像谱中利用色散滤波器提取海浪波数能量谱,估流精度直接影响色散滤波器性能,实际中准确估流较为困难[5],另外调制传递函数与雷达机制有关,不同雷达调制传递函数不同,这对于推广应用带来难度,操作难度提高通用性降低。而阴影图像反演法避开这一复杂处理过程,它是基于海浪在雷达回波中各种物理调制特性映射到了海杂波散射模型,具备几何光学粗糙面某些特性,通过图像处理提取海浪参数[16]。1990年, Wetzel[6]利用理论分析海面假设为高斯面,分析低掠射角入射下的海面后向散射模型,利用散射强度来估测波高,奠定图像法反演波高的理论基础。1995年,Henschel[7]等人利用实测实验数据来验证Wetzel模型,并取得一定成果,然而由于缺乏大量数据与校验,波高估测误差较大。1998年,J.R Buckley等人[8]对Henschel估测方法的局限性原因进一步分析,通过利用归一化雷达目标有效截面校验阈值,使得量测范围变大、精度提高。2000年,R. Gangeskar[9]通过大量实验提取图像灰度方差反演波高,相关系数为0.9,算法的精度得到很大提升。2001年,Buckley[10]通过仿真实验来揭示观测值与Wetzel理论值间偏差原因,并利用不同位置上的回波强度来校验阈值,精确估计了不同海况下的有效波高;进一步从理论上证实了阈值随作用距离发生变化的。2012年 W. J. Plant[11]研究了极化方式对几何阴影与局部阴影调制问题,实验结果表明局部阴影是海杂波阴影图像中主要组成部分;W.J.Plant深度剖析了阴影成因的问题,为日后精确的检测阴影提供支撑。2014年,Rune[12][16]通过分析W.J.Plant的实验发现工程应用中,难以从图像中辨别两种阴影的影响的主次,通过大量数据分析,仿真试验得出且两种阴影差异较小, Rune基于随机粗糙面几何阴影理论利用边缘检测提取图像中阴影阈值,获取有效波高,算法提升了估测精度,降低试验成本及简化试验流程。2017年,卢志忠等[15-16]利用实测雷达图像数据分析Rune结论,发现阴影阈值随着海况变化。2017年,卫延波博士[17]采用自适应分块以及浅水条件修正等改进策略改进几何阴影法反演有效波高,提高了有效波高的估测精度。2019年,Giovanni Ludeno等[18]基于原始雷达图像和相应的非校准波高图像之间的相关性,利用比例因子改变波高图像的幅度,建立雷达成像的数学模型。通过分析Rune的实验结果发现阴影比例随着海况而变化,而在掠射角小于2°区域的这种变化最明显,对大量实验分析发现波高与阴影比例间存一定线性关系,还需要通过大量实验数据验证。
本文在Rune的研究基础上,结合图像处理技术及统计学分析,研究不同波高下阴影比例的差异,用统计分析最小二乘拟合固定区域下阴影比例与波高间的线性模型,用拟合模型估测原始数据的波高,最终将估测的波高与参考波高作比较来检验算法的可靠性与可行性。
1 x-波段雷达图像阴影估测波高
1.1 低掠射下的海面图像
海洋运动学上认为海面是由多种随机波动叠加而成,在电磁散射模型中海面构造为二维随机粗糙面。将二维粗糙表面(例如海面、沙漠,戈壁等)简化成一维粗糙表面模型[14],降低研究杂度,增加工程实用性。
低掠射下的海面由亮暗条纹组成,本文提出的波高反演策略基于粗糙面理论的延拓。如图1所示为原始雷达图像。

图1 原始雷达图像
1.2 估计图像阴影边缘
估测阴影阈值,先提取图像阴影边缘。利用边缘检测找到阴影边缘。
1.2.1 图像阴影边缘检测
通过对雷达图像单一方向上做像元卷积运算式(1)获取图像梯度[12][16]。算子如式(2)依次对雷达图像相邻的8个方向上分别进行卷积运算。右侧卷积为
IE1(r,θ)=I(r,θ)⊗H1(r,θ)
(1)
其中I(r,θ)是极坐标表下原始雷达图像,r是径向斜距,θ是方位角,IE1(r,θ)是左侧算子。像元差分算子给出
(2)
绘制原始图像频率曲线取前M%图像的像素值作为阈值,遍历原始雷达图像,然后利用H1~i算子做卷积得到图像梯度IE1~IE8。
以IE1中的第i幅边缘图像的阈值求取为例
(3)
N%为IE1映射到图像中前N%的灰度值,之后每个方向的边缘图像叠加成一个合成的边缘图像IT,将各方向上边缘图像做和[12][16]
(4)
1.2.2 剔除孤立点及奇异值
对于孤立点去除利用边缘比较法将每个点与阈值τF做比较
(5)
1.2.3 提取阴影边缘区域
(6)
(7)
其中Ips为可疑阴影边界,If为阴影边界[12]。
1.3 阴影阈值求取及获取阴影比例
通过对海杂波雷达图像作个方向边缘检测得到If,绘制If的灰度直方图。If映射到原始雷达图像η中,并获取统计直方图FH(η),对直方图取众数,即可得到阴影灰度阈值τS[12]为
τS=mode(FH(η))
(8)
将用阈值τS将原始图像分割成阴影区与非阴影区并求取阴影比例Rs(γ)。
(9)
对图像处理结果分析发现,低掠射角下区域面积变化较大,通过观察了大量图像数据发现阴影比例大小与波高有关。因此选取掠射角小于10°,L×L个像素的区域求取阴影比例为
(10)
其中L为区域尺寸,SIs为所选区域内阴影面积。
1.4 利用最小二乘拟合波高关系式
通过假设有效波高与阴影比例呈线性关系,目标函数即为
Hs=A+B·Rs
(11)
最小二乘拟合有效波高关系式,目标函数定义为
(12)
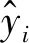
根据最小二乘法的计算原理[15],可以得到标定系数A和B的估计值为
(13)
2 数据实验分析
从2007年至今,哈尔滨工程大学在国家某装备项目资助下积极开展航海雷达监测海浪、海流、海面风场、近岸水深、波面高度、溢油及海冰等方面的应用研究,先后在北海、黄海、东海、南海等地开展科研试验,积累了大量实测数据。实验航海雷达为X波段机扫导航雷达、天线为杆式端馈开槽波导,天线转速:26+2、-6/min,参数如表1所示,信号带宽为20 MHz,分辨率为径向7.5 m、角度向0.1°,雷达图像回波强度是0~-2.5 v,A/D变换后映射为0~8191范围内,图像帧时间约2.5 s,岸基天线架设高度为45 m、船基为25 m。

表1 X波段导航雷达参数
本文选取数据源于2010~2013年期间东海海域实测数据共210组,数据具有多种海况,遮挡小,图像质量好,具有一定代表性。所选岸基与海上数据的风速在15 m/s左右,海上波高范围为3~4 m,岸基为2 m左右。由于远区杂波竞争等因素,故本文选取的径向图像上限为2000 m,剔除遮挡因素角度向范围为60°左右。原始数据采集由于雷达架设的高度不同,因此相同掠射角下所选择的径向距离点数不同。根据仿真要求选择掠射角2~10°间的区域。所以岸基选1200~1700 m,舰载选600~1100 m作为数据处理区。
图2是8个方向卷积之后叠加输出结果。

图2 经过卷积后八幅叠加的梯度图像(风速为13.26 m/s,波高4.0 m)
将图像前N%=10%的像素值作为梯度阈值检测边缘,用τF=6去除孤立点。通过灰度直方图前H=30%判别获得过渡区(阴影边缘),最后建立边缘的直方图统计取众数得到阈值τS,如图3所示。

图3 直方图注:较高大的曲线为所选区域的直方图曲线,较低的内部曲线为边界直方图曲线,虚线是所得的阈值。
通过大量的数据试验重复上述方法求得阴影比例值,用Rune方法绘出波高与照度间的曲线。图像表明在不同波高下掠射角越大阴影比例差异越小,掠射角越小在相同掠射角下阴影比例差异越大,特别是在有效掠射角范围1~3°内最为显著,而小于1°的范围内背景噪声较大故不作考虑。


图4[16] 波高与照度曲线注:左边在有效波高为2 m,风速高于4 m/s,右边有效波高4 m,风速15 m/s,明显看到在有效的掠射角范围1~10°阴影比例随波高变化最显著是1~3°。
获取阈值求取阴影比例后,将wavex测得的波高为外部参照。本文用了200组数据其中有10组海上数据,海上数据选取波高值大都在3 m以上,风速在15 m/s左右,剩余的都是岸基数据,岸基海况上述已作介绍。利用其中一半数据来拟合直线,利用最小二乘法式(12)、式(13)估测出式(11)中A=0.693、B=2.83剩余的数据用来检验。拟合效果如图5所示。
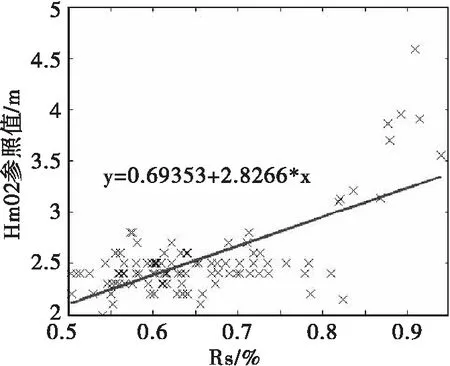
图5 利用最小二乘法拟合的直线注:横坐标表示阴影比例、纵坐标表示有效波高。
利用最小二乘法得到线性关系式来估测有效波高,通过关系式反演的有效波高与外部参考波高作比较,评价算法可靠性,如图6所示。

图6 算法估测值Hm02与外部参考值比较
本文算法得到波高与外部参考波高求相关系数为0.89,均方根误差为0.42,方差为0.21。通过比较统计参数得出本算法能准确估测雷达图像波高,而且参照值偏差较小,满足估测精度要求。
3 结束语
目前对于有效波高的估测在工程上较为成熟的算法是谱分析法。图像统计法大多停留在实验阶段,本文算法得益于信噪比求波高启发,在图像统计法中应用线性关系结合外部参照来反演有效波高。
并利用实测雷达图像数据来检测算法精度,通过外部参考统计分析得到其相关系数为0.89,均方根误差为0.42,方差为0.21。
试验结果表明:阴影比例与有效波高之间满足线性关,利用线性关系式能准确估测有效波高,文献[16]中提出假设得到验证,算法具有可行性与有效性。
然而由于数据有限算法仍有不足,算法没有考虑电磁波散射模型对图像阴影调制的影响。雷达极化方式、电磁波长、粗糙度等对阴影的作用。还需要进一步考虑不同海域,低海况,低风速等条件下算法适用性及可靠性。
