超Sober空间与k-有界Sober空间的性质

唐 友, 杨金波

(江西师范大学 数学与信息科学学院, 江西南昌330022)

§1 引言与预备

序与拓扑之间有着紧密的联系. 给定一个偏序集, 其上有许多经由偏序定义的拓扑, 称之为偏序集上的内蕴拓扑, 如“单边”拓扑上拓扑, 下拓扑, Scott拓扑, Alexandroff拓扑及“双边”拓扑区间拓扑, Lawson拓扑, 双Scott拓扑等等. 偏序集上的序结构影响着其上内蕴拓扑的性质,比如连续偏序集上的Scott拓扑是局部紧的. 另一方面, 给定一个拓扑空间, 其开集族在集合的包含序下是一个“天然的”Frame; 若(X,τ)是一个T0拓扑空间, 定义x ≤τ y当且仅当x ∈cl{y},则(X,≤τ)为一个偏序集, 称≤τ为空间(X,τ) 的特殊化序(specialization order). 拓扑空间的性质也影响着相应序结构的性质, 比如: 若X为局部紧空间, 则其开集Frame是连续格.

Sober空间在非Hausdroff拓扑与Domain理论中扮演着重要角色, 其定义是由既约集给出的. 拓扑空间X的一个非空子集F称为既约的, 若对任意闭集A,B,F ⊆A ∪B蕴含着F ⊆A或者F ⊆B. 既约集与定向集之间有着紧密的联系. 一方面, 对于给定的T0空间, 在其特殊化序下,X中的定向子集是既约集; 另一方面, 对于任意偏序集P, 其Alexandroff空间(P,γ(P))中的既约集恰好为偏序集P中的定向集. 基于这一重要观察并结合偏序集P上Scott拓扑的定义,文[1]在更为一般的T0拓扑空间中引入了由既约集诱导的拓扑的定义, 因而偏序集上的Scott拓扑恰好为其上Alexandroff拓扑空间中既约集所诱导的拓扑. 为了刻画空间中既约集所诱导拓扑的性质, 文[1]引入了超Sober空间与k-有界Sober空间的概念并得到许多有意义的结果. 比如T0空间X中由既约集诱导的拓扑与原拓扑一致当且仅当X为k-有界Sober空间; 对定向完备偏序P而言,γ(P)是超Sober的,γ(P)是k-有界Sober的,γ(P)是Sober的以及σ(P)是超Sober的四者等价等等.

从另一角度来看, 由于Sober空间在非Hausdroff拓扑与Domain理论中的重要地位, 比Sober空间更强的超Sober空间以及作为Sober空间推广的k-有界Sober空间本身就具有研究的价值.本文将进一步研究超Sober空间与k-有界Sober空间的性质, 厘清超Sober拓扑,k-有界Sober拓扑与T2,T1,T0拓扑以及Sober拓扑之间的关系. 下文将讨论它们的乘积空间, 子空间的性质,超Sober空间,k-有界Sober空间在连续映射下的保持性以及对Smyth上幂空间构造的封闭性.特别地证明了一个空间为超Sober空间当且仅当其Smyth上幂空间为超Sober空间; 若拓扑空间X的Smyth上幂空间为k-有界Sober空间, 则空间X为k-有界Sober空间; 一族k-有界Sober空间的积空间仍为k-有界Sober空间.

对给定的集合X记X(<ω)为X的有限子集之全体. 对任意x ∈X, 记O(x)为点x的开邻域系.设P为偏序集,D ⊆P称为定向的, 若对任意d1,d2∈D, 存在d ∈D, 使得d1,d2≤d. 设X是拓扑空间,X的全体开集记为O(X). 任意A ⊆X,A在X中的闭包记为clA, 在涉及多个空间时为区分起见也记作clXA.

文中涉及的记号与术语可参见[2-4]. 对于给定的T0拓扑空间, 除非特别说明, 本文涉及到的与偏序相关的所有概念, 其偏序都是指X上的特殊化序.

定义1.1(见[1, 4]) 设X为拓扑空间,F为X的非空子集.

(1) 称X为Sober 空间, 若对拓扑空间X的每一既约闭集F, 存在唯一x ∈X, 使F=cl{x}.

(2) 称X为超Sober空间, 若对拓扑空间X的每一既约集F, 存在唯一x ∈F, 使得F ⊆cl{x}.

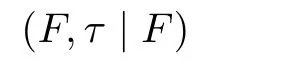
的既约集.

命题1.2若X为拓扑空间,F ⊆X.F是X的既约集当且仅当clF是X的既约集, 从而clF是X的既约闭集.

推论1.2设f是拓扑空间X到拓扑空间Y的连续映射, 若F为X的既约闭集, 则clY f(F)为Y的既约闭集.

§2 超Sober空间

本节进一步讨论超Sober空间的性质, 厘清超Sober拓扑与T2,T1,T0拓扑以及Sober拓扑之间的关系, 将证明一个空间为超Sober空间当且仅当其Smyth上幂空间为超Sober空间.

由超Sober空间的定义容易看出, 超Sober空间是Sober空间, 从而是T0空间. 另一方面, 单位闭区间[0, 1]上赋予Scott拓扑是Sober的. 令F= [0,), 则F是既约的, 但是对任意x ∈F,Fcl{x}=[0,x], 因而[0, 1]不是超Sober空间.命题2.1设X为拓扑空间. 则

(1) 若X为超Sober空间, 则X为T0空间. 进一步,X为超Sober空间当且仅当X为T0空间并且对X中任意既约集F, 存在x ∈F使得F ⊆cl{x}.

(2) 若X为T2空间, 则X为超Sober空间.

(3) 若X为只有有限个点的T0空间, 则X为超Sober空间.

证 (1) 显然.

(2) 设X为T2空间, 以下说明X中的既约集只能是单点集. 假设X的既约集F包含两个不同的点y,z, 由X为T2空间, 存在开集U,V使得x ∈U,y ∈V且U ∩V=∅. 于是

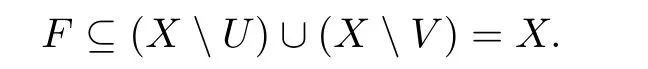
由F为既约集,F ⊆X U或者F ⊆X V. 若F ⊆X U, 则由x ∈F,x/∈U, 与x ∈U矛盾.若F ⊆X V, 则由y ∈F,y/∈V, 与y ∈V矛盾.

注2.1(1) 超Sober空间不必为T2空间. 设X={a,b},τ={∅,{a},X}. 则(X,τ)为T0但非T1(从而非T2)空间. 由命题2.1(3), (X,τ)为超Sober空间.

(2) 上述例子也说明了存在超Sober但非T1的空间.

(3) 存在T1但不是超Sober的空间. 设X为无限集, 其上赋予有限补拓扑. 则X为T1空间. 由于X为空间中的既约闭集, 但对任意x ∈X,cl{x}={x}. 因此X不是Sober空间, 从而X不是超Sober空间.

下述命题表明, 超Sober性是可遗传的.

命题2.2超Sober空间的子空间是超Sober空间.

命题2.3超Sober空间的连续收缩是超Sober空间.

证 设X为超Sober空间,Y为X的连续收缩核. 于是存在连续映射f:X →Y,g:Y →X使得f ◦g=idY, 由X为超Sober空间,X为T0空间, 又由Y为X的连续收缩核, 于是Y为T0空间. 设F为Y的既约集, 由g连续,g(F)为X的既约集. 又X是超Sober空间, 存在x ∈g(F)使得g(F)⊆clX{x}, 于是f(x)∈f ◦g(F)=F, 从而

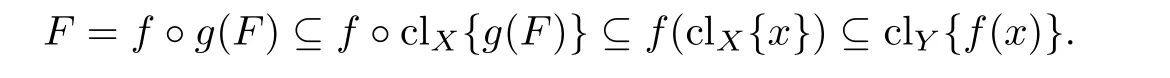
推论2.1设(X,τ)为超Sober空间,f: (X,τ)→(X,τ)为连续映射且f为幂等映射, 即f ◦f=f, 则(f(X),τ|f(X))为超Sober空间.

引理2.1(见[5]) 设X为Sober空间,C,U分别为X中闭集与开集,A为Qv(X)中的既约集.引理2.2(见[5]) 设X为拓扑空间,K ⊆X,A ⊆Q(X). 若对X中任意开集U,K ⊆U当且仅当存在Q ∈Q(X)使得Q ⊆U, 则K ∈Q(X).

命题2.4(见[5]) 设X为拓扑空间,A,B ⊆X,B为X的一个基, 则下述条件等价.

(1) clA=clB;

(2) 对X中的任意开集U,∅当且仅当∅;

(3) 对任意∅当且仅当∅.

命题2.5设X为拓扑空间,A,B ⊆X,B为X的一个基, 则下述条件等价.

(1) clA ⊆clB;

(2) 对X中的任意开集U, 若∅, 则∅;

(3) 对任意U ∈B, 若∅, 则∅.

定理2.1设X为T0空间, 则X为超Sober空间当且仅当其Smyth上幂空间Qv(X)为超Sober空间.

证 设Qv(X)为超Sober空间,F为X中的既约集. 令ηX(=):X →Qv(X). 由ηX连续,{↑x:x ∈F}为Qv(X)中既约集. 又由Qv(X)为超Sober空间, 存在K ∈{↑x:x ∈F}使得{↑x:x ∈F}⊆clQv(X){K}, 于是

§3 k-有界Sober空间

本节讨论k-有界Sober空间的性质. 从k-有界Sober空间的定义容易知道, Sober空间为k-有界Sober空间,k-有界Sober空间为T0空间. 注意到T1空间中的特殊化序为离散序, 因此T1空间中只有单点集的上确界是存在的, 故T1空间为k-有界Sober空间.

定理3.1(见[1]) 若P为连续偏序集, 则(P,σ(P))为k-有界Sober空间.

注3.1上述定理表明:

(1)k-有界Sober空间不一定为Sober空间. 取P为非定向完备的连续偏序集, 则(P,σ(P))不是Sober空间.

(2)k-有界Sober空间不必为T1空间. (R,σ(R))不是T1空间.

§3 小结

在非Huasdorff空间与Domain理论中, Sober空间是一类非常重要的空间. 本文主要从拓扑的角度讨论了超Sober空间与k-有界Sober空间的一些基本性质. 结果表明超Sober空间与k-有界Sober空间这两类空间也具有许多类似于Sober空间的良好性质. 由于超Sober空间比Sober空间强,k-有界Sober空间比Sober空间弱, 因此对这两类空间性质的讨论有助于加深对Sober空间的认识. 如何从序结构的角度刻画关于其上内蕴拓扑为超Sober空间,k-有界Sober空间的偏序集的性质是值得探讨的研究内容.