预应力作用下单箱单室箱梁剪力滞效应研究

晏 继 伟

(兰州局集团有限公司职工培训中心，甘肃 兰州 730050)

1 概述

预应力混凝土箱梁桥截面特性良好，整体性强，能有效抵抗弯矩和剪力[1]。预应力技术的引入，使得混凝土结构的变形被有效控制，裂缝的产生被推迟，构件的刚度得到提高，结构的耐久性得到改善，有助于改善旅客乘车的舒适性，提高列车高速运行时的安全性，满足后期运营期间对线路平顺性的要求。因此，这种结构被广泛使用于桥梁建设中。PC箱梁由于其空间构造特点，将会产生剪力滞效应。近些年，中外研究人员做了大量关于箱梁的剪力滞效应的研究，但对于预应力引起的箱梁剪力滞效应，相关研究还不完善。乐小刚[2]、项贻强[3]、季文宇[4]等通过ansys软件分别建立了预应力作用下的箱梁模型，使用等效荷载法，获取了剪力滞系数，得出了一些关于预应力作用下的箱梁剪力滞现象的规律。

桥梁模型实验是一种探索桥梁结构力学特性的有效手段，可以与理论研究相互印证。本文使用有机玻璃材料制作了单箱单室箱梁模型，进行了相关力学试验。试验时，在预应力束中设置压力传感器控制荷载大小，在跨中架设百分表测量梁体挠度，在典型截面处布置应变片获取结构应变。本文在进行预应力荷载对单箱单室箱梁剪力滞效应的影响程度理论研究时，使用等效荷载理论，将预应力转化为一般外荷载进行计算。然后，引入剪力滞翘曲位移函数[5]，即梁的纵向位移u(x,y,z)，以准确反应箱梁的挠曲变形。使用能量变分法研究剪力滞效应时，需根据最小势能原理求解挠度和应力的解析解，计算解析解时剪力滞翘曲位移函数的选取很重要。这里使用三次剪力滞翘曲位移函数，根据现有文献，三次模式精确度已经很高。

2 控制微分方程

2.1 基本假定

本文研究预应力作用下的箱梁剪力滞效应的方法为能量变分法，并基于以下各项基本假定[6-10]。

1)在翼板应变能计算时，假定板平面外的剪切变形、翼板竖向应变及横向应变很小，可以不计入位能。

2)腹板在对称荷载作用下，变形特性符合平截面假定。

3)箱梁横截面中性轴位置在对称荷载作用下，形心位置按照初等梁理论计算。

从理论上来说，箱形结构梁桥在发生弯曲变形时，截面中性轴的实际位置与基于初等梁理论的截面形心不再重合，因此需引入一个附加轴向位移[11]。

4)假定梁截面内力沿纵向的分布不受剪力滞的影响，剪力滞只改变梁截面正应力的分布。

5)箱梁腹板轴向变形采用平截面假定，在压弯荷载作用下，在计算结构总应变能时不计算轴向变形产生的应变能。

6)定义w(x)为箱梁横截面上任一点(x,y,z)的竖向弯曲挠度，w′(x)为该处的转角，u(x,y,z)为纵向位移，U(x)为翼板剪切变形最大差，M(x)为沿梁长x处的截面弯矩，Q(x)为沿梁长x处的截面剪力。

箱梁截面示意图见图1。

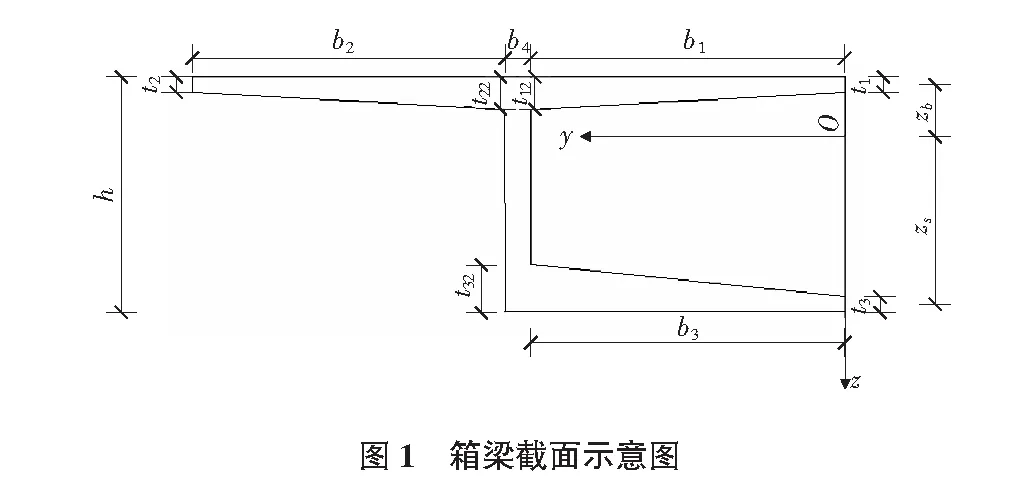
根据文献[12]～[14]，选择三次抛物线形函数f(y,z)为剪力滞翘曲位移函数，如下:

(1)

2.2 势能表达式

用式(2)表示横截面纵向位移u(x,y,z)，该式将剪力滞效应考虑在内。

u(x,y,z)=-zw′+f(y,z)U(x)

(2)

考虑截面纵向变形，可计算截面正应变ε、剪应变γ分别为：

(3)

(4)

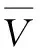
(5)

将式(3)，式(4)代入式(5),可得：

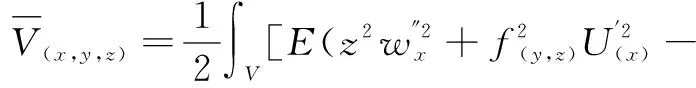
(6)

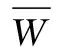
(7)

由式(6)和式(7)可得总势能∏表达式为：

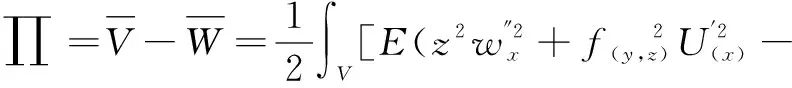
(8)

通过最小势能原理可知，梁段在外力作用下产生位能，对总位能∏取变分，值为0。

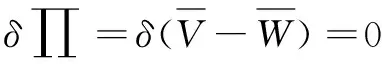
(9)

2.3 控制微分方程组

考虑预应力箱梁剪力滞效应，结合式(8)，式(9)两式进行变分计算，可得出控制微分方程和边界条件为：

(10)

由式(10)前两式可得:

(11)

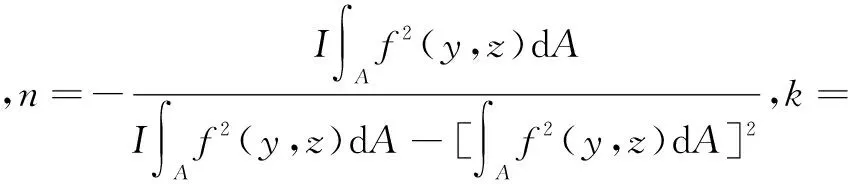
2.4 边界条件

此处针对典型简支梁边界条件进行求解分析。对于固定端，边界条件为：

U(x)=0,δU(x)=0

(12)

对于非固定端假设梁端，边界条件为：

(13)

2.5 剪力滞应力计算式

考虑式(2)，结合胡克定律，截面任一位置纵向应力σ(x,y,z)为：

(14)

由式(14)可知，剪力滞现象在跨中位置不存在。

3 剪力滞效应缩尺模型实验概况

3.1 箱梁基本情况及材料特性

桥梁模型实验是一种探索桥梁结构力学特性的有效手段，现制作跨度L=1 m的有机玻璃等截面箱梁模型，横截面如图2所示。选用公称直径3 mm的低松弛、高强钢丝线作为预应力筋。

为获取有机玻璃材料真实力学参数，预制试件，进行力学拉伸实验，得到模型所用材料弹性模量E=2 600 MPa，泊松μ=0.385。

3.2 加载装置及测点布置

实验采取双点对称加载的方法，两侧对称布置预应力钢束，荷载大小通过每束束筋中布置的压力传感器进行控制。实验加载情况如图3所示。

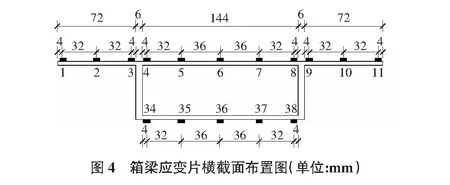
实验时，把应变片布置于典型截面处。在跨中、L/4跨以及L/8跨顶板共设置27个应变测点，三处横向位置相同，于底板处设置15个应变测点。在紧邻锚固端的L/8跨处设置一组应变测点，以获取应力从预应力锚固端向跨内传递过程中的应力扩散特征，箱体横截面应变测点布设位置见图4。

实验时，使用精密百分表位移计测量各种实验工况下的挠度变形情况，并根据百分表的指针变化幅度辅助判断梁体变形是否达到相对稳定。读取应变读数时，位置计读数波动值需在精度范围之内。百分表位移计设置在跨中腹板与底板相交处，挠度测试见图5。

4 实验结果与分析

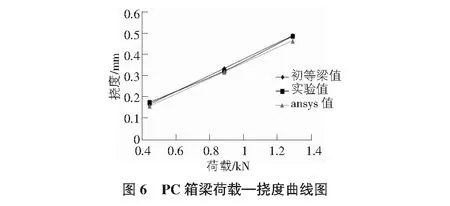
4.1 荷载—挠度关系

实验梁体跨中位置荷载—挠度变化情况见图6。从中可以发现，有限元解与实验解相接近，说明了实验解和本文理论解的精度很高；同时可以看出如果不计算剪切变形引起的挠度增大，仅按初等梁理论计算，得出的挠度值往往偏小。

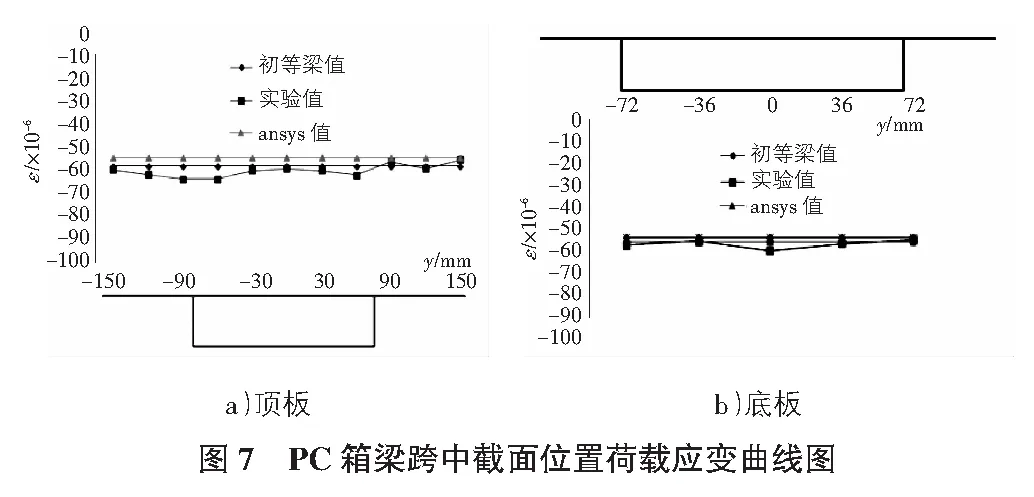
4.2 横桥向应变分析

从图7中可以看出，跨中顶、底板截面各点处实验值有波动，考虑到实验值的离散型，结合有限元解及初等梁解进行数据分析，可以发现此截面各点纵向应变均匀，不存在剪力滞现象。这是由于跨中截面距离受力点较远，处于纯弯曲受力状态，结果亦符合前文理论推导。

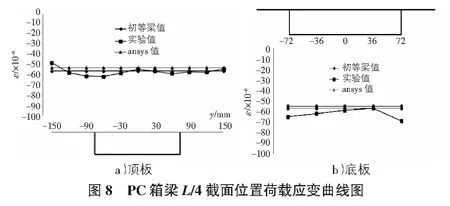
图8为梁体L/4位置处应变分布情况，可以看出，该截面应力变化也不存在剪力滞特点，与跨中应变的分布相比，该位置数据方差大于跨中位置，存在一定离散型。

图9为L/8截面处应变分布情况，该截面应变值变化较大，按照初等梁理论得出的应变值与真实应变值最大相差29%，可知此位置处存在显著的剪力滞现象，而且顶板变化程度要高于底板。

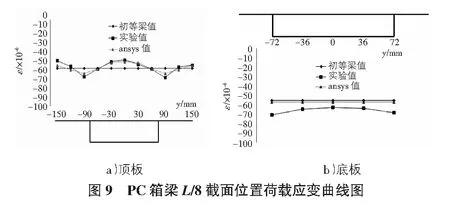
4.3 顺桥向应变分析

从图10中可以发现，改变梁体顶底板预应力束布置位置，则相关受力点附近的应力会产生很大变化。现对梁体顶板、腹板相交点展开研究，分析沿梁长方向纵向应力的分布规律，探究梁体轴力位置变化与箱梁的剪力滞现象的关联性。

如图11所示，当预应力作用在顶板时，沿梁长方向腹板与顶板交界点处的纵向应力并非均值，梁端处应力值明显大于跨中；当靠近作用点时，截面应力明显增大，最大值为初等梁值的3倍。

如果改变预应力束筋布置位置，则会引起梁端一定范围Le内横截面应力的改变，此范围Le约等于梁体结构腹板间的间距。此范围之外各处应力值与初等梁计算值一致，横截面应力值沿梁长方向均匀分布，不存在剪力滞效应，可将梁体视为纯弯曲受力状态；同时，预应力束位置的变化不会引起此范围内截面应力值的变化。

5 结语

1)本文所用实验系统能够有效模拟预应力作用下箱梁的受力情况。本文制作了缩尺单箱单室模型，以预应力等效荷载理论为依据，模拟了预应力箱梁受力特征，并使用自行设计的实验加载装置进行了各项试验，得出了各项试验数据，所得数据与本文理论解，有限元板壳数值解，初等梁理论解相一致。

2)总体来看，梁端至一定范围Le内，截面应力值与初等梁计算值不一致，越接近梁端，两者偏差越大，最大处在梁端，两者相差3倍。如果距梁端位置大于Le，则初等梁计算值与截面实际应力值相一致。另外，预应力直线束筋位置的改变会影响梁体中梁端至一定范围内Le内的应力的分布。

3)总体来看，当预应力束筋按直线形式对称布置时，单箱单室PC箱梁不存在剪力滞现象，而梁端附近的横截面应力变化是力的应力传递路径导致的。当PC箱梁中预应力束筋按照直线形式布设时，梁体L/8截面应力变化很大，L/4截面应力分布不均匀，跨中位置和初等梁解相同，没有剪力滞现象产生。

4)在箱梁中布置预应力筋能大幅度提高梁体承载能力，预应力筋在设计时一般会选择集中布置，这会导致布束点附近存在明显的应力集中现象，梁端处应力值会剧烈变化，如果只是按照初等梁理论简单计算，布束设计时不考虑该因素，会使得梁端顶板、底板处梁体开裂，引起桥梁病害。