结构力学中位移法与力矩分配法的关系分析★

姚展环 杨 威 冯章标 凌志丹 农妍妹

(北部湾大学建筑工程学院，广西 钦州 535011)

0 引言

目前，计算超静定结构的精确方法主要是位移法，位移法的思想是法国的纳维于1826年提出的，其基本未知量包括节点的角位移和独立节点的线位移。但现实中大多数为多层多跨的结构体系，有多个未知量，需要列多个位移法方程来求解。H.克罗斯于1930年在位移法的基础上，提出了不必解方程组而是逐次逼近的力矩分配法，大大地减轻了工程的计算工作。位移法和力矩分配法的共性和特性给我们提供了一个建立二者关系的视角。两者都需借助不平衡力矩以及查询形常数表和载常数表来获取形常数载常数来计算结构内力。但两者性质不同，位移法是精确解法，是以节点的角位移和独立节点的线位移作为基本未知量。而力矩分配法是近似解法，主要是通过对刚节点施加阻止转动的约束得到各固端弯矩，并分配传递至各刚结点平衡。

通过研究位移法的计算过程，引入曲率半径、转动刚度、分配系数和传递系数将位移法求解过程中的方程消除，从而得到不必解算联立方程的近似解法——力矩分配法。本文将以例题展开讨论位移法和力矩分配法之间的关系。

1 位移法计算过程

位移法是以结构的结点位移为基本未知量；以结点和截面的平衡方程为基本方程，据以求出结点位移；最后求出结构的内力。其最大的特点在于：位移法的思路是先通过加入附加联系固定所有独立结点位移，此时各附加联系上将产生附加反力(不平衡反力)，为消除这些附加反力，同时放松各结点(即同时取消所有附加联系)，从而同时消除各附加联系上的附加反力。若附加联系不止一个，则必须求解联立的位移法典型方程[3]。

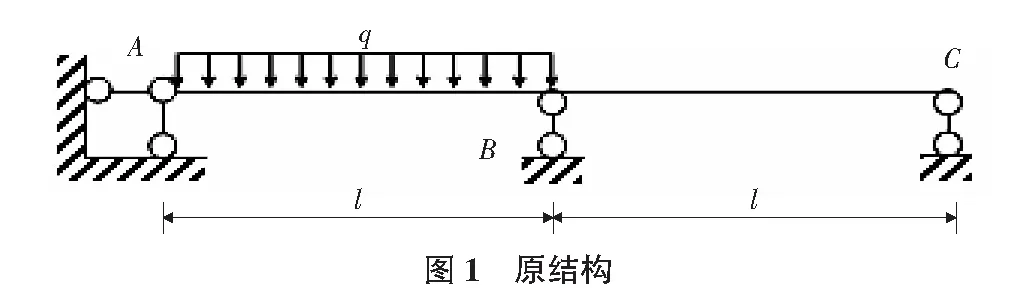
例题：用位移法计算如图1所示连续梁的弯矩。

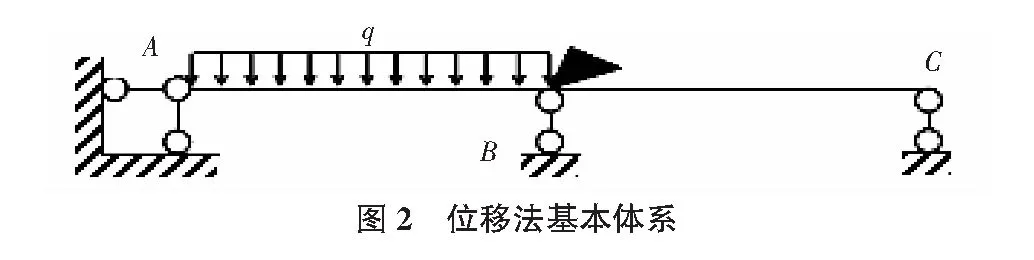
1)基本体系(见图2)：

2)位移法方程：

k11Δ1+F1P=0

(1)

其中，Δ1为连续梁结点B角位移；k11为基本结构在单位转角Δ1=1作用下在附加约束中的约束力矩；F1P为基本结构在荷载作用下在附加约束中的约束力矩。

3)计算k11,F1P(见图3～图6)：

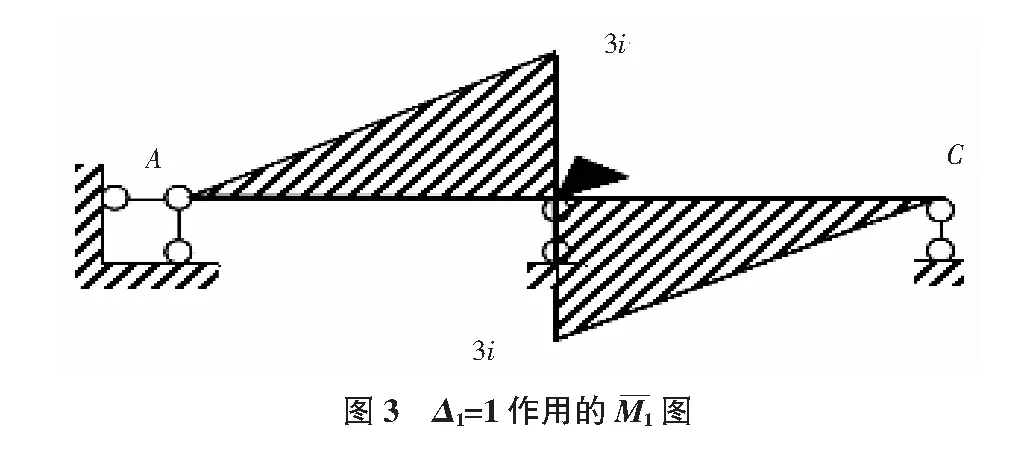
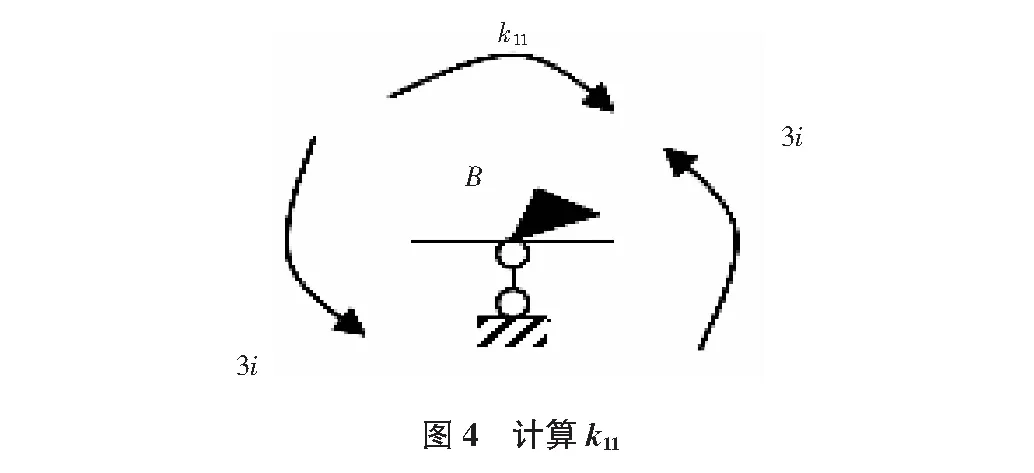
由结点B的力矩平衡可得：

∑MB=0，k11=3i+3i=6i

(2)

由结点B的力矩平衡可得：

∑MB=0，F1P=ql2/8

(3)

4)计算Δ1:

Δ1=-F1P/k11=-ql2/48i

(4)

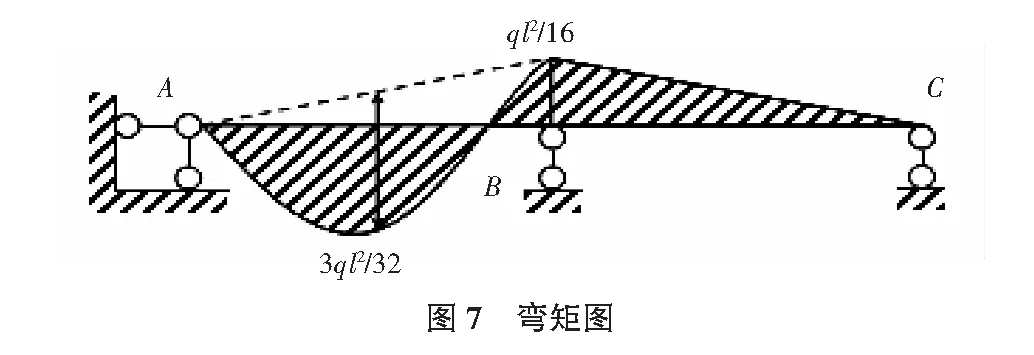
5)作M图(如图7所示)：由弯矩的叠加原理：

(5)

MBA=3i×(-ql2/48i)+ql2/8=ql2/16

(6)

MBC=3i×(-ql2/48i)=-ql2/16

(7)

其中，MBA为AB杆的B端弯矩；MBC为BC杆的B端弯矩。

2 力矩分配法计算过程

力矩分配法的求解思路则有所不同，第一步先约束所有独立结点角位移，得到基本结构，显然各结点将产生不平衡力矩。为了使基本结构转化为原结构，必须消除各结点不平衡力矩(因为原结构中不存在这些不平衡力矩)[3]。

由例题，

1)先在B结点加上阻止转动的约束(见图8)：

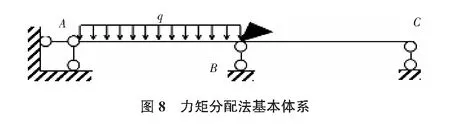
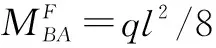
(8)

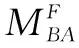
2)松开结点B：

相当于结点B施加一个力偶荷载-ql2/8。

转动刚度：

SBA=3iBA=3i

(9)

BBC=3iBC=3i

(10)

其中，SBA为AB杆B端的转动刚度；SBC为BC杆B端的转动刚度。

分配系数：

μBA=SBA/(SBA+SBC)=3i/(3i+3i)=0.5

(11)

μBC=SBC/(SBA+SBC)=3i/(3i+3i)=0.5

(12)

其中，μBA为AB杆在B端的分配系数;μBC为BC杆在B端的分配系数。

∑μ=μBA+μBC=1

(13)

分配弯矩：

(14)

(15)

传递弯矩均为0。

即：

(16)

(17)

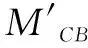
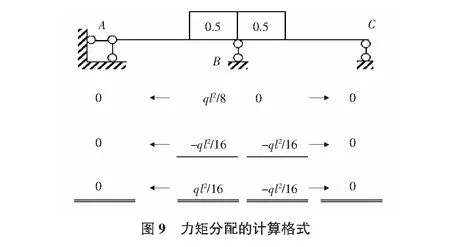
∑MB=ql2/16-ql2/16=0

(18)

3 位移法与力矩分配法关系分析

位移法与力矩分配法均运用了不平衡力矩，都借助不平衡力矩来计算结构内力。两者都需要查询形常数和载常数表来获取形常数载常数以便计算。

由式(2)，图4可知：

k11=∑i

(19)

由式(3)，图6可知：

F1P=-M

(20)

由式(4)，式(19)，式(20)得：

Δ1=-F1P/K11=M/∑i

(21)

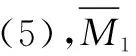
(22)

由式(21)，式(22)可得：

(23)

由曲率K表示单位弧段上切线转过角度的大小作如下定义：

K=Δα/Δs

(24)

其中，K为杆件中性层的曲率；Δα为转角增量;Δs为弧长增量。

由曲率与曲率半径的互为倒数的关系有：

K=1/ρ

(25)

其中，ρ为杆件中性层的曲率半径。

由式(24)，式(25)得：

1/ρ=Δα/Δs

(26)

或：

Δα=Δs/ρ

(27)

由转动刚度S为单位转角所需的力矩作如下定义：

S=M/Δα

(28)

由杆件的弯矩：

M=EI/ρ

(29)

其中，E为材料的弹性模量；I为杆件截面的惯性矩。

由式(27)～式(29)得：

S=M/Δα=(EI/ρ)/(Δs/ρ)=EI/Δs

(30)

由可变形固体的小变形假设由Δs≈1，因此得：

S=EI/Δs≈EI/l=i

(31)

由力矩分配系数μ为同一刚结点上的某一根杆的转动刚度与所有杆的转动刚度和的比值，作如下定义：

μ=Si/∑Si=ii/∑i

(32)

由式(23)得分配弯矩：

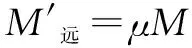
(33)

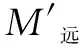
对于等截面杆件，由于均匀性假设与影响线，可知同一杆件弯矩变化为线性变化，由相似原理，与传递系数C表示当杆件近端产生转角时，杆件远端弯矩与近端弯矩的比值作如下定义，即：

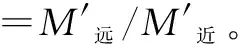
得：

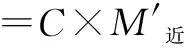
(34)

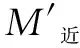
因为位移法中荷载在基本结构中相应截面上所产生的弯矩MP与力矩分配法中在节点加上阻止转动的约束后由荷载产生的固端弯矩MF均由等截面直杆的载常数可查得，即：

MP=MF

(35)

由式(33)，式(35)：

(36)

其中，M′为远端或近端的分配弯矩。

故位移法与力矩分配法的计算结果相同。

对于多结点的体系，由于其处于平衡状态，即每个结点的内力与外力合力为0，所以当结点合力不近似于0时，不为0的合力矩继续传递直至结点合外力近似等于0。最终累加各杆端所得的分配弯矩可得各杆端弯矩。

4 结语

位移法是通过平衡条件建立位移法方程，取隔离体来计算不平衡力矩。而力矩分配法是在位移法的基础上引入曲率半径、转动刚度、分配系数与传递系数将位移法求解过程中的方程消除，所以力矩分配法不需要列方程，只需按照分配系数来分配不平衡力矩，但计算过程相对繁杂，需要很强的细心及耐心。

致谢：本文是在蒋琼明博士的指导下完成的，在此表示深深的感谢。