引信后坐质量-弹簧系统动态特性与设计

居荣誉，王雨时，闻 泉

(南京理工大学 机械工程学院， 南京 210094)

引信后坐质量-弹簧系统主要包括后坐保险机构和后坐针刺发火机构。其中后坐保险机构靠后坐质量(惯性筒等)受到的后坐力解除保险。而后坐针刺发火机构则是火帽独自或装在火帽座上在发射时受到后坐力的作用与击针相撞或击针在发射时受后坐力作用与火帽相撞而发火[1]。在引信中，特别是在炮弹引信中，引信后坐质量-弹簧系统应用极为广泛。

文献[2-4]中采用卷积积分并结合计算机编程计算出引信后坐保险机构的位移响应与速度响应;文献[5]中采用半周期正弦函数拟合加速度过载，运动常规数学知识复杂地求解出了某枪榴弹引信单自由度后坐保险机构的位移响应，并结合计算机仿真研究了后坐过载系数对位移响应的影响;文献[6]中运用了MATLAB软件编写四阶龙格-库塔法程序解算了引信双自由度后坐保险机构的位移响应，进而深入地研究了引信双自由度后坐保险机构的运动特性。

目前对于引信后坐保险机构运动微分方程的求解通常采用计算机编程的方法，此方法需要具备常微分方程数值求解知识，并且所得结果均为数值，不直观。对以上问题，本研究拟应用拉普拉斯变换的方法求解引信后坐质量-弹簧系统运动微分方程，并总结各设计参数对引信后坐质量-弹簧系统保险与解除保险的影响，为引信精准设计提供参考。

1 引信单自由度后坐质量-弹簧系统动力学建模[5]

1.1 引信单自由度后坐质量-弹簧系统物理模型

引信经典单自由度后坐保险机构如图1所示，主要由惯性筒1、保险球2(被保险件)、本体3和惯性簧4等组成。发射时，惯性筒和惯性簧受后坐力作用。刚开始，后坐力较小不足以克服惯性簧抗力使惯性筒移动。随后后坐力不断增大，到一定值后，惯性筒开始克服惯性簧抗力移动。当惯性筒向下运动到一定位置时，释放保险球，此时后坐质量-弹簧系统解除保险。

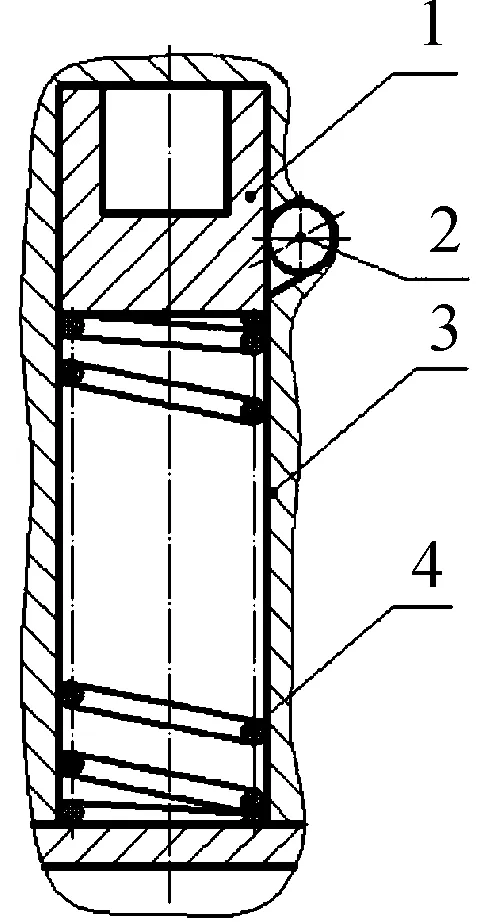
图1 单自由度后坐质量-弹簧系统示意图

弹丸意外跌落时，惯性筒和惯性簧受跌落冲击惯性力作用。在小的跌落冲击过载下，跌落冲击惯性力不足以克服惯性簧抗力，惯性筒不移动；在大的跌落冲击过载下，惯性筒和惯性簧克服惯性簧抗力向下运动。但由于跌落冲击惯性力作用时间短或峰值较低，惯性筒还没运动到解除保险位置就在惯性簧的作用下恢复原位了，从而保证了勤务处理阶段弹丸暨引信意外跌落时的安全。

1.2 引信单自由度后坐质量-弹簧系统数学模型

在对单自由度质量-弹簧系统建立数学模型前，先作如下简化假设：单自由度后坐质量-弹簧系统可看成理想的无阻尼振动系统；在机构运动过程中惯性簧刚度恒定;本模型只考虑垂直运动，不考虑系统横向摆动的影响。

上述单自由度后坐质量-弹簧系统向下运动时的受力状态如图2所示。在后坐质量-弹簧系统刚受到后坐过载作用时，惯性筒受惯性簧的抗力R、后坐力Fs以及摩擦力Ff和Ff′的作用而保持静止。故有[6]：

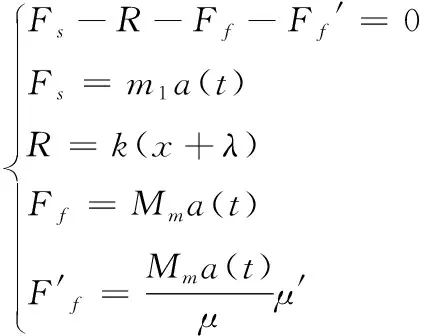
(1)

式中:m1为惯性筒质量与惯性簧三分之一质量之和；R为预压惯性簧对惯性筒的作用力;Fs为惯性筒和惯性簧所受后坐力之和；a(t)为发射或跌落时外加冲击激励而产生的弹丸暨引信的加速度；k为惯性簧的刚度系数；λ为惯性簧装配预压量；x为惯性筒从初始位置向下运动的位移量；Ff为保险球受外加激励作用对惯性筒壁产生的摩擦力；Ff′为惯性筒驻室侧壁对惯性筒产生的摩擦力；μ′为驻室侧壁与惯性筒之间的摩擦系数；保险球的等效后坐质量Mm=m2μsin2α，其中μ为保险球与惯性筒之间的摩擦系数；α为保险球导向孔轴线与引信轴线夹角；m2为保险球质量。

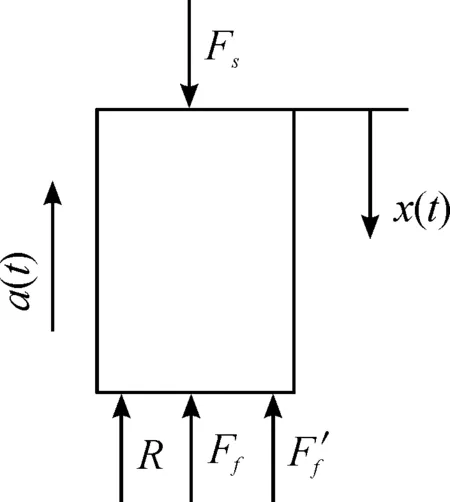
图2 单自由度后坐质量-弹簧系统惯性筒受力分析

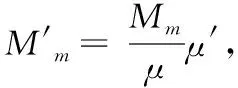
(2)

当t>t0时，惯性筒开始运动，应用牛顿定律并整理后得惯性筒运动微分方程：

(3)

2 应用拉普拉斯变换法求解引信后坐质量-弹簧系统位移响应方程

拉普拉斯变换法通常用于线性振动系统的分析，求解线性微分方程十分有效，该方法既适用于求解瞬态振动，又适用于求解强迫振动[7-8]。引信单自由度后坐质量-弹簧系统实际上就是一种强迫振动的单自由度振动系统，因此运用拉普拉斯变换法来对引信后坐质量-弹簧系统位移响应方程的求解可能会很有效。

据文献[9]，为了研究方便通常将膛压P上升段简化为余弦函数，该方法使用简便且精度较高，适用于引信初期设计。作者曾试用Vallier公式简化、Logistic函数简化法和线性插值拟合法等方法对82 mm口径迫击炮榴弹、122 mm口径加农炮榴弹和76 mm口径加农炮杀伤榴弹的膛压曲线进行拟合，但都存在精度不高或运算复杂、使用不便等问题。下文采用余弦简化法对弹丸弹压曲线进行拟合：

(4)

式中：P0为弹丸挤进压力，滑膛炮通常取P0=0，线膛炮的通常取P0= 30 MPa[9];Pm为最大膛压值;tm为最大膛压处时刻;t为膛压持续时间。

弹丸在最大弹压点之前的加速度可表示为[9]：

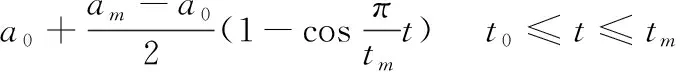
(5)

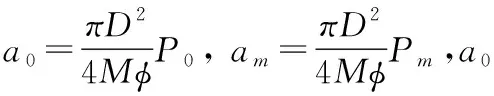
对于弹丸跌落过载曲线，该类过载曲线通常为近似正弦曲线，因此同样可以用余弦函数进行拟合：

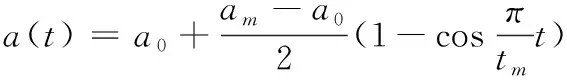
(6)

将式(5)和式(6)代入到式(3)中，并进行整理得：

t0≤t≤tm

(7)

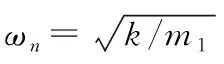
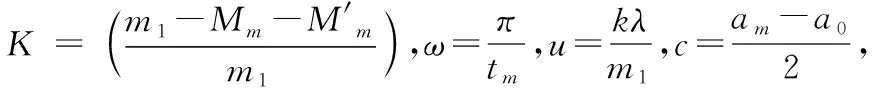
t0≤t≤tm

(8)

对式(8)进行拉普拉斯变换[10-11]，得到：

t0≤t≤tm

(9)

式中：S为复变量；F(S)为拉普拉斯变换中的象函数。

t0≤t≤tm

(10)

对式(10)进行拉普拉斯逆变换，整理得：

t0≤t≤tm

(11)

t0≤t≤tm

(12)

式(11)与式(12)即为用拉普拉斯变换法求得的引信单自由度后坐质量-弹簧系统位移响应和速度响应。

3 算例计算与ADAMS软件仿真验证

应用ADAMS软件中的ADAMS/view模块建立仿真模型如图3所示。定义惯性筒和保险球的质量，在惯性筒与底座之间建立弹簧，并添加弹簧的刚度与预压量等参数，对本体与底座施加固定约束，对惯性筒与引信体间施加移动副。取自文献[12-13]中的3组引信典型的内道弹和冲击环境数据，以及文献[14-15]中的两组引信后坐质量-弹簧系统结构参数分别如表1和表2所列。摩擦因数μ和μ′参考文献[16]中取为0.20和0.25。

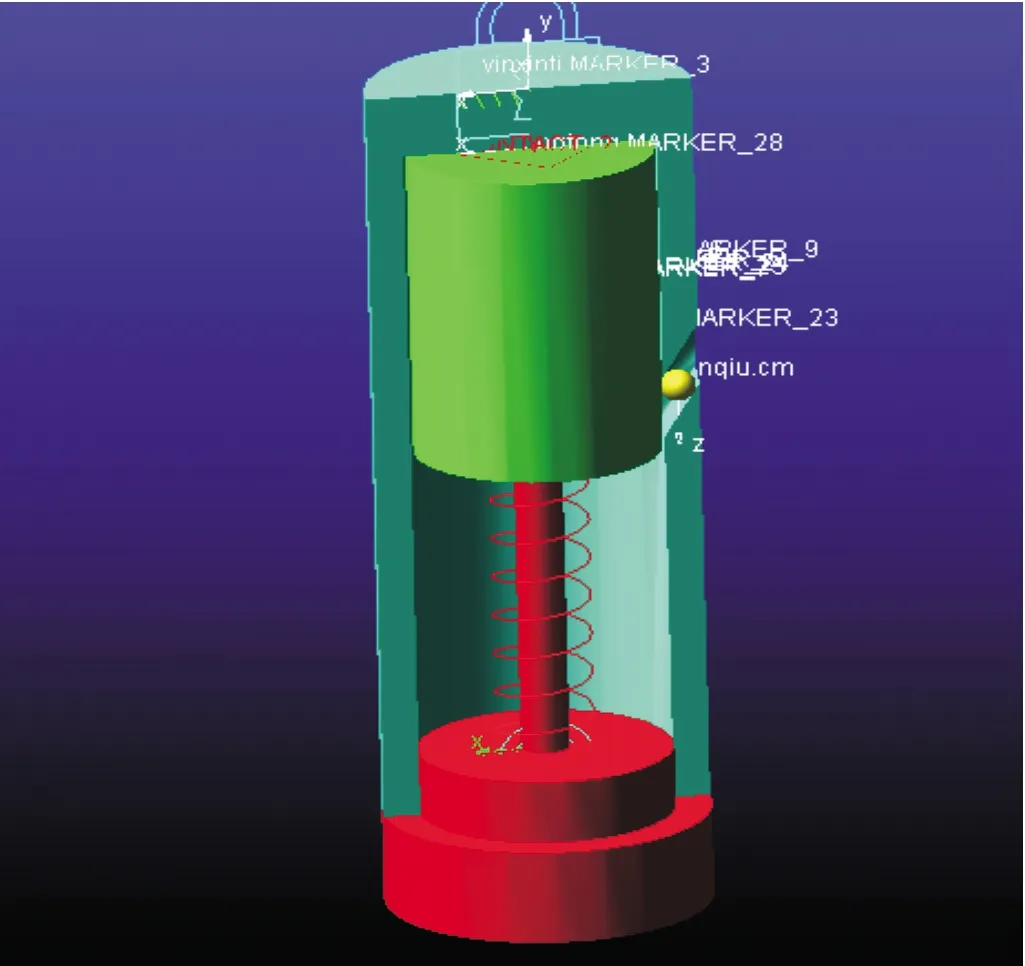
图3 引信后坐质量-弹簧系统ADAMS软件仿真模型

将上述参数代入式(11)得后坐过载函数，将其施加到惯性筒质心。其函数为：

(13)

式中：F为施加在惯性筒上的后坐过载力(N)；tm为发射或跌落最大加速度处的时刻(s) ；d*time为ADAMS“角度制”算法标志。

设置好软件中发射状态与跌落状态下的仿真时间和仿真步数，运用ADAMS软件分别对表2中的两组参数进行仿真，惯性筒在两种冲击过载环境下的位移响应曲线如图4和图5所示。

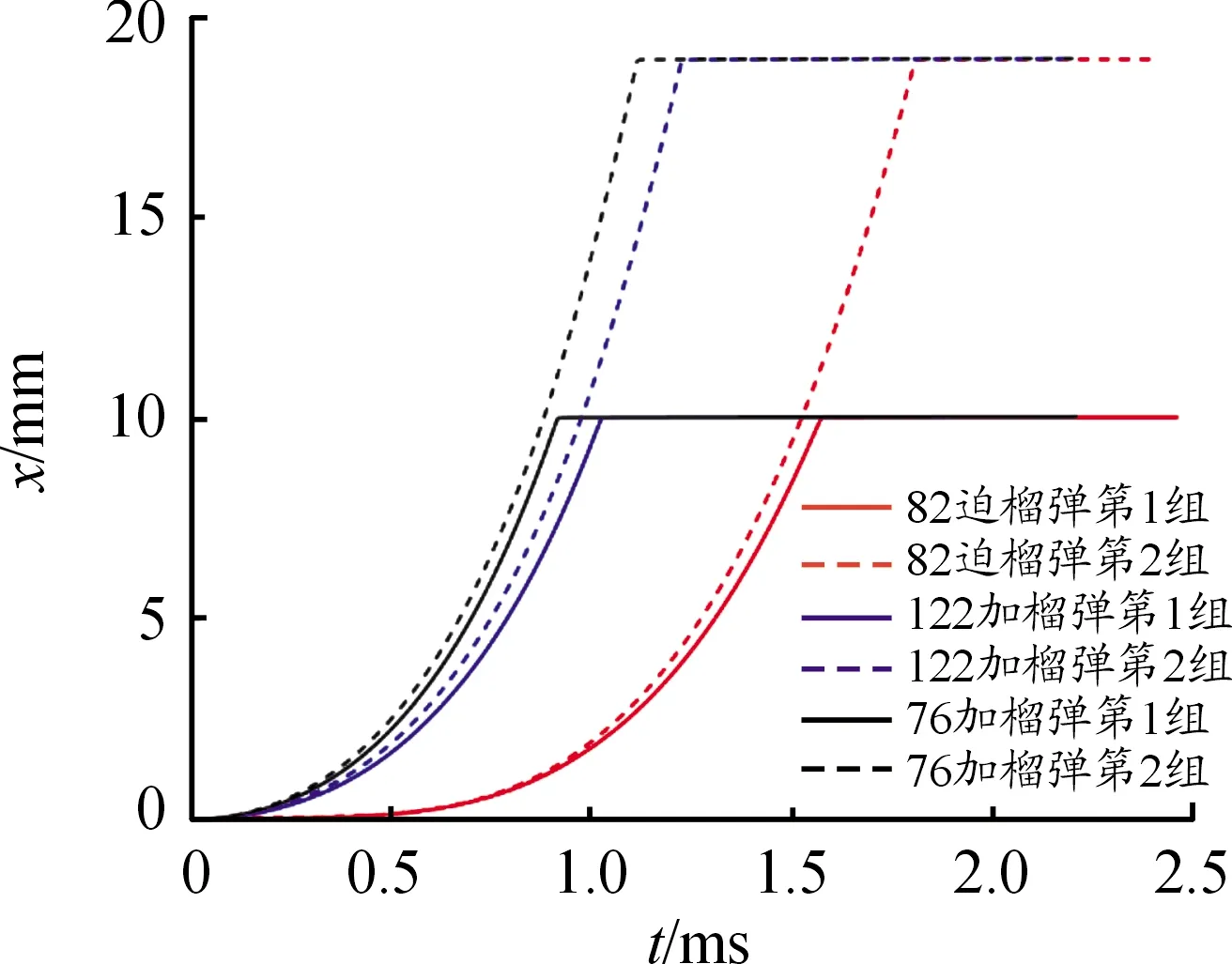
图4 发射状态下惯性筒位移响应曲线

将表1和表2数据代入式(11)，理论计算出惯性筒发射与跌落状态下的位移x3和x4，应用四阶龙格-库塔法数值求解微分方程得到两种位移x5和x6，应用ADAMS软件仿真得到两种位移x1和x2，均已列入表3中。

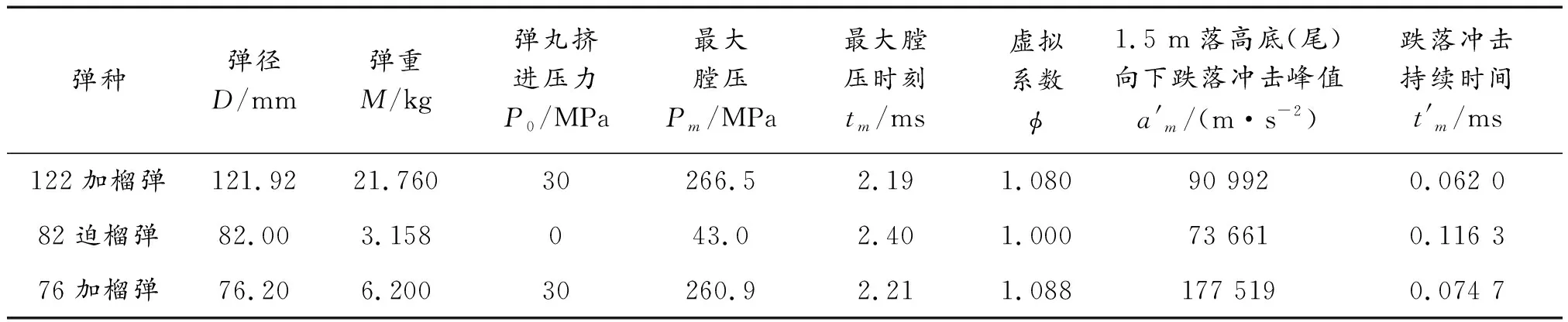
表1 3种弹丸的内弹道与跌落冲击数据

表2 两种引信后坐质量-弹簧系统文献算例的结构设计参数

表3 发射与跌落状态下机构解除保险性能理论计算与仿真值

由表3可看出，在发射与跌落两种状态下，应用拉普拉斯变换法解得的位移响应结果与应用四阶龙格-库塔法和ADAMS软件仿真得到的结果基本一致(最大误差1.30%)，说明拉普拉斯变换法可以适用于求解机构强迫振动情况下的位移响应，且此方法运算简便，误差小，可为引信初期设计计算提供参考。误差原因可能是仿真过程中忽略了惯性簧的质量，也可能是摩擦系数取值与Adams软件自动选取结果有差异所致。

4 引信后坐质量-弹簧系统解除保险性能影响因素分析

对于引信后坐质量-弹簧系统来说，良好的保险和解除保险性能主要体现在：在发射时，后坐质量(如惯性筒等)位移足够大，保证解除保险足够可靠；另一方面在意外跌落时，后坐质量(如惯性筒等)的位移要尽可能地小，以提高勤务处理安全性。

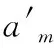
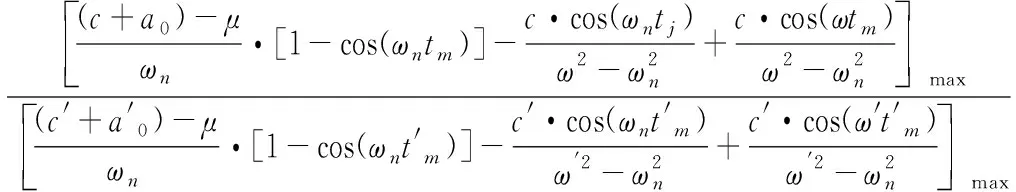
(14)

对于此优化设计方程的求解问题从理论上归根到底还是要对f(m1,m2,k,λ,μ,μ′,α)进行偏微分，寻求极值点，然后通过极值点关系判断单调性。但是此方法过于繁琐，且计算量很大，因此采用数值计算方法，通过计算机编程，运用冒泡法对f进行排序和绘图，找出f关于各影响因素的单调性，从而分析各影响因素对引信后坐质量-弹簧系统保险和解除保险性能的影响。

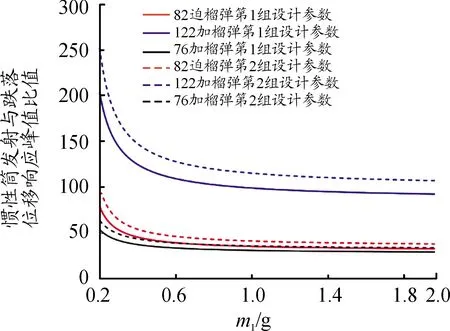
图6 惯性筒质量m1值的目标函数曲线

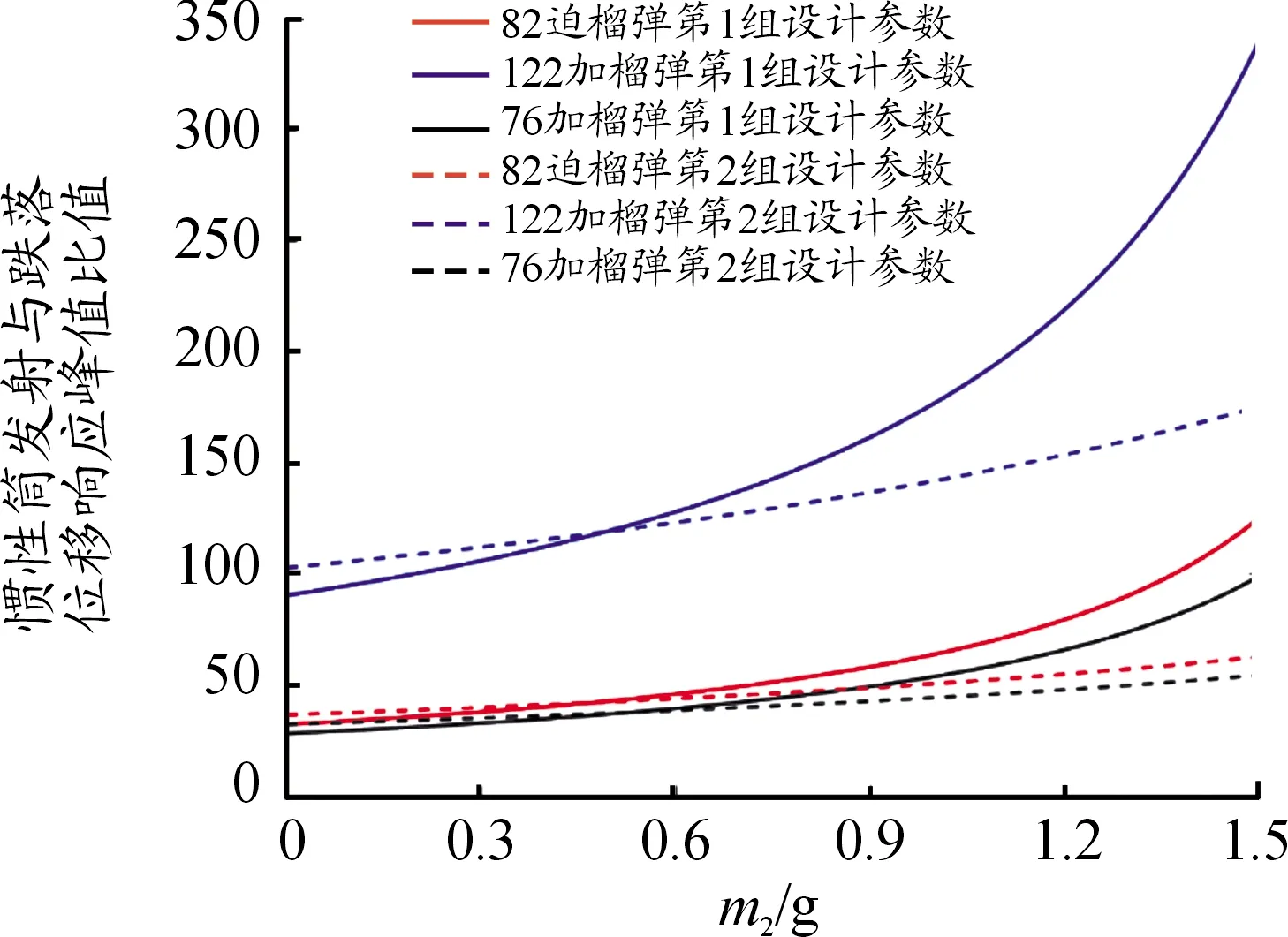
图7 保险球质量m2值的目标函数曲线

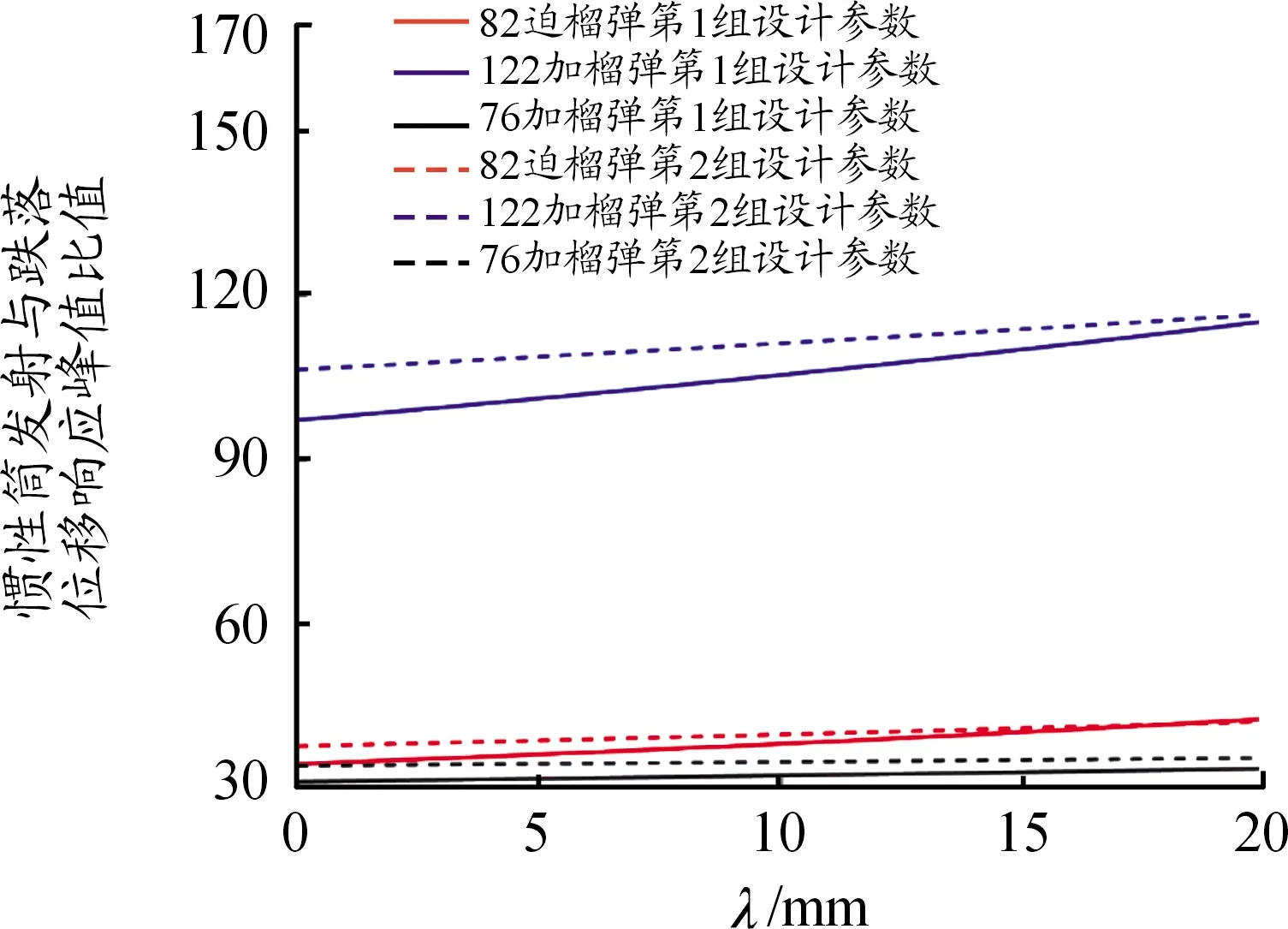
图8 装配预压量λ值的目标函数曲线

图9 弹簧刚度系数k值的目标函数曲线

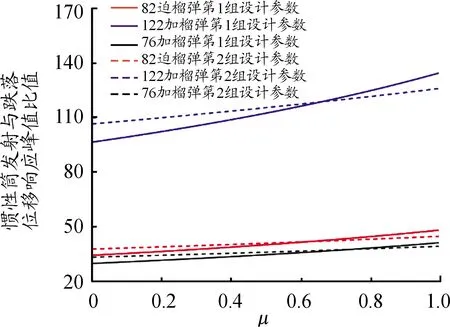
图10 摩擦因数μ值的目标函数曲线

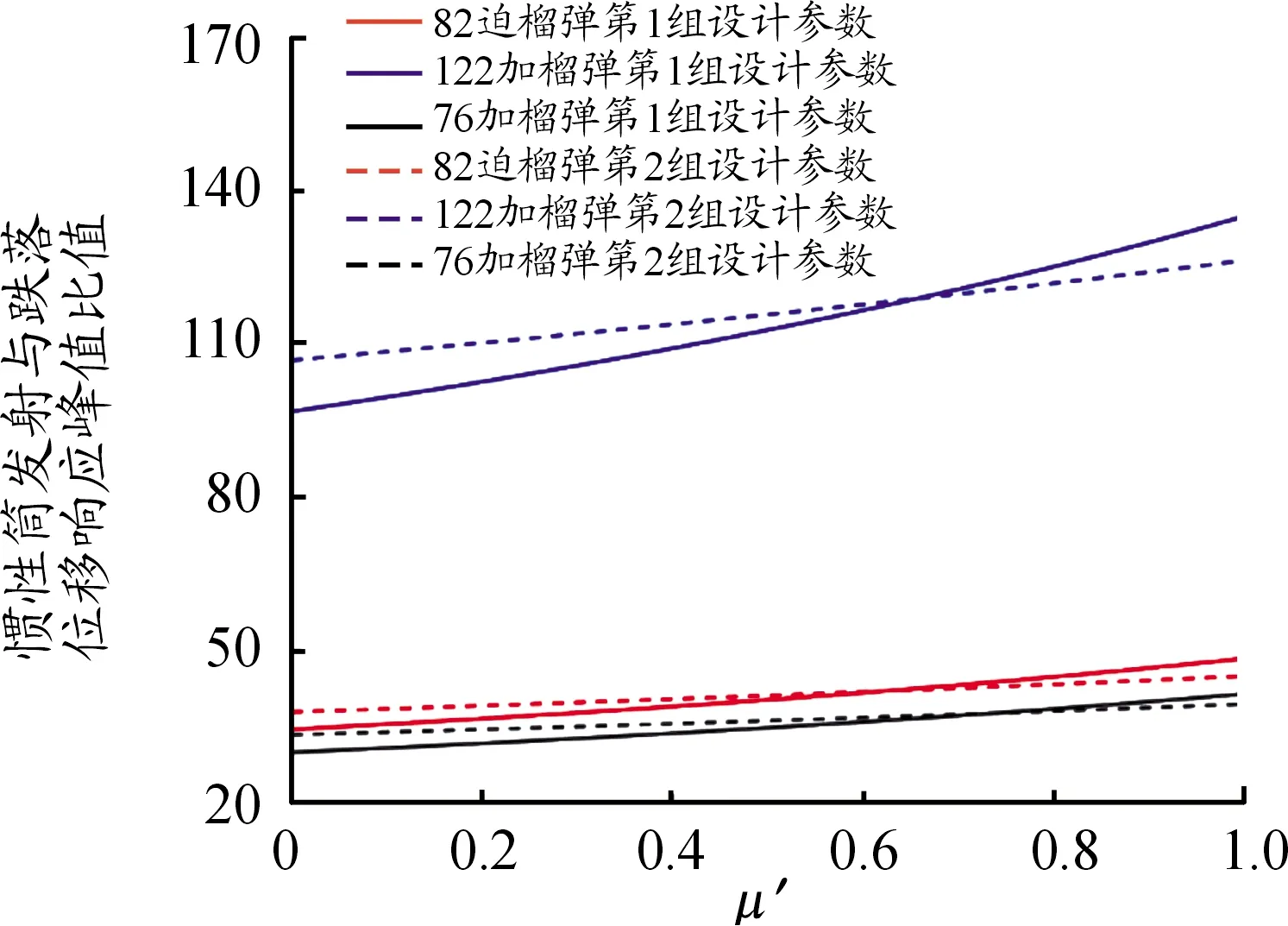
图11 摩擦因数μ′值的目标函数曲线

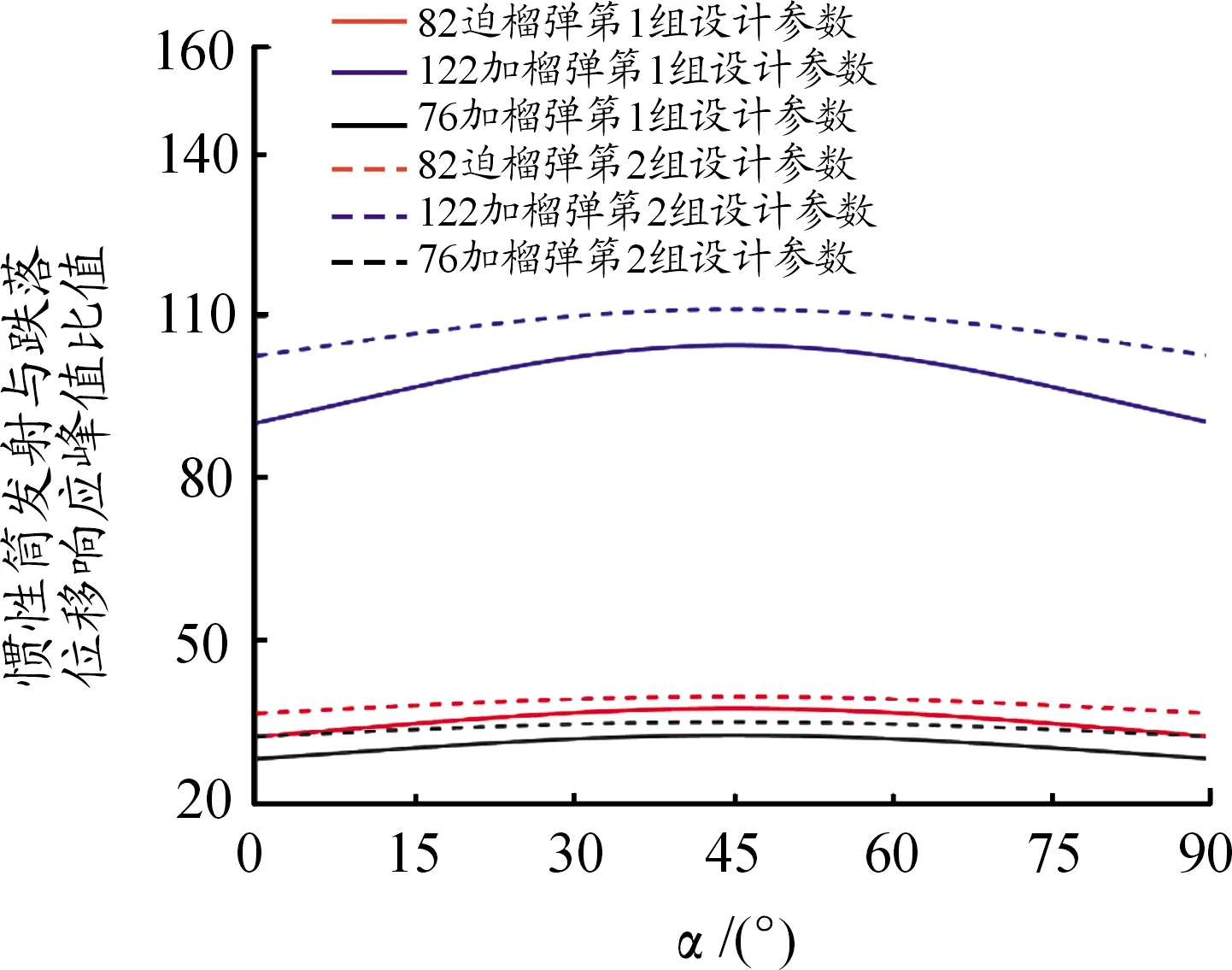
图12 α值的目标函数曲线

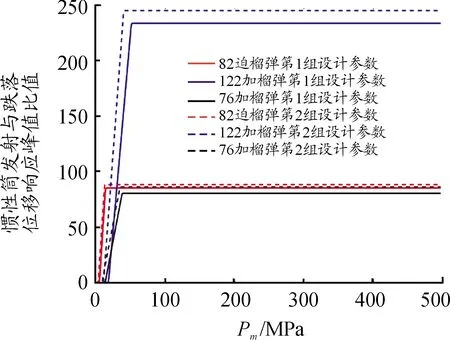
图13 Pm值的目标函数曲线

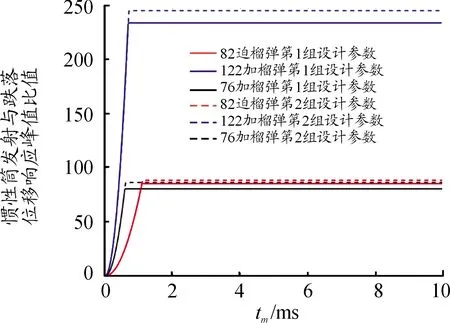
图14 tm值的目标函数曲线

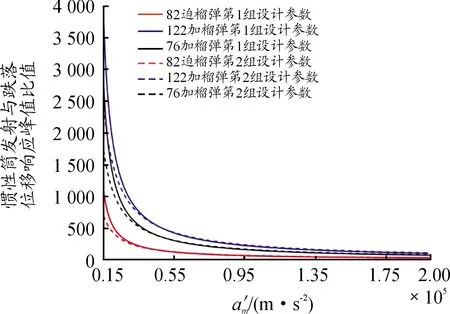
图15 跌落冲击过载值的目标函数曲线

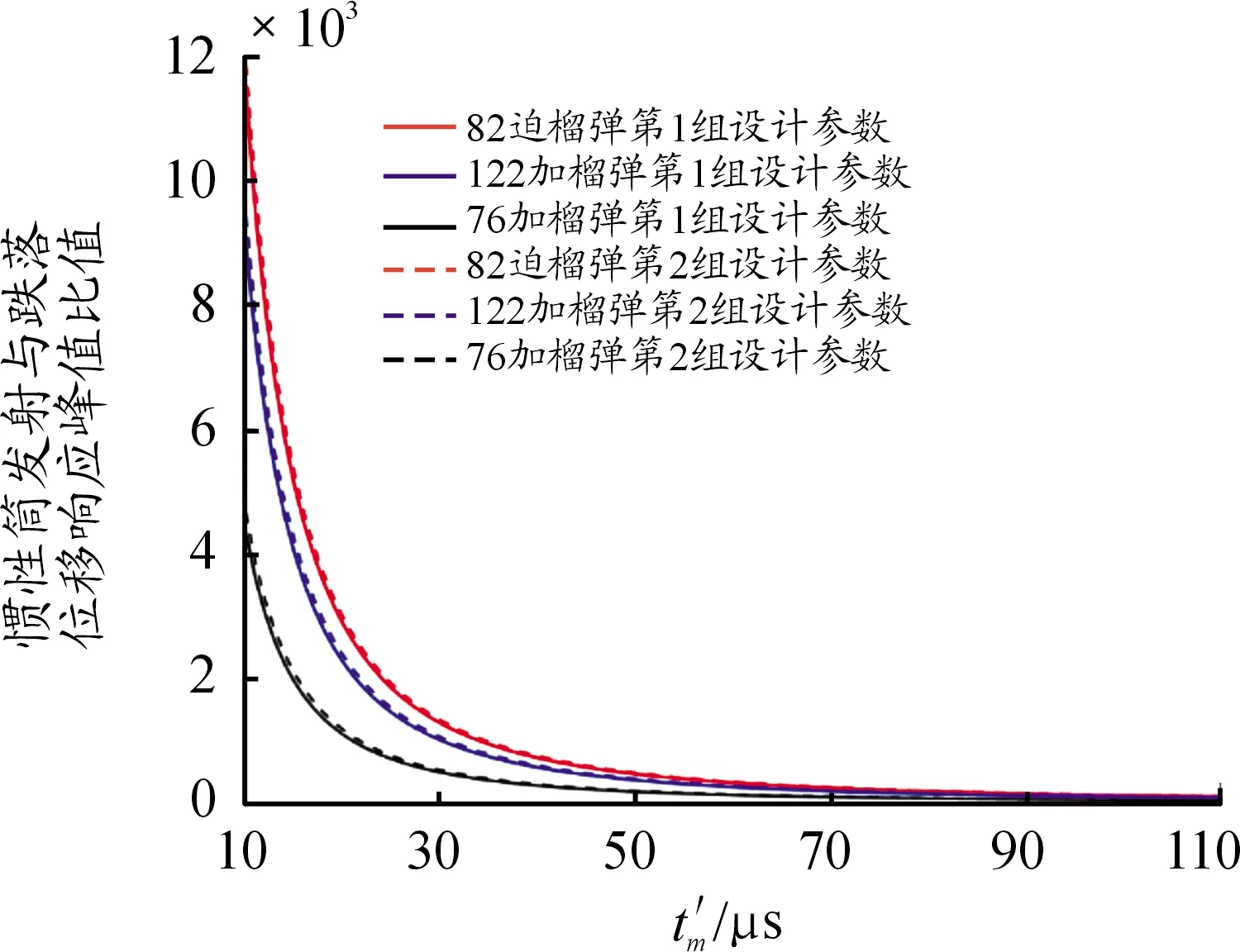
图16 跌落冲击持续时间值的目标函数曲线

上述分析结论都是以82 mm口径迫击炮榴弹、122 mm口径加农炮榴弹和76 mm口径加农炮榴弹引信后坐保险机构为例得出的。从目标函数值的变化规律看，适当增大保险球质量m2、惯性簧装配预压量λ、惯性簧刚度系数k、保险球与惯性筒间摩擦系数μ、驻室侧壁与惯性筒间摩擦系数μ′，减小后坐等效质量m1，以及将保险球导向孔轴线与引信轴线夹角α设计为45°都有利于解决引信后坐质量-弹簧系统发射时解除保险与跌落时不解除保险之间的矛盾。此外，弹丸发射膛压高、膛压作用时间长、避免勤务处理时意外跌向软目标，也有利于解决引信后坐质量-弹簧系统发射时解除保险与跌落时不解除保险之间的矛盾。

5 结论

拉普拉斯变换法适用于求解引信后坐质量-弹簧系统的运动微分方程，使用简便且计算精度高，适用于引信初期的设计计算；从工程设计角度来说，适当减小后坐质量m1，适当增大惯性簧装配预压量λ、惯性簧的刚度系数k、将保险球导向孔轴线与引信轴线夹角α取为45°都有助于解决引信后坐质量-弹簧系统发射时可靠解除保险与跌落时不解除保险之间的矛盾。