高中数学向量四心问题的解题技巧
2020-10-11姜勇钢
姜勇钢
(江苏省海门市第一中学 226100)
一、四心的定义和基本关系
在这里,我们所强调的“四心”主要是指在一个三角形当中的重心、垂心、外心和内心.重心是三角形三条中线的交点,我们通常用G来表示;而垂心是三角形三条高线的交点,用H表示;外心是三角形三条中垂线的交点,用O表示;内心就是三角形的三条角平分线的交点,用I表示.以下面这个三角形为例,三角形的重心、垂线、外心、内心在三角形中的大致位置如图所示,在此三角形中,三角形的四心都是有不同的向量表示的,现给大家整理了这样一些结论,更方便同学们在学习的时候快速记忆.具体表示如下:
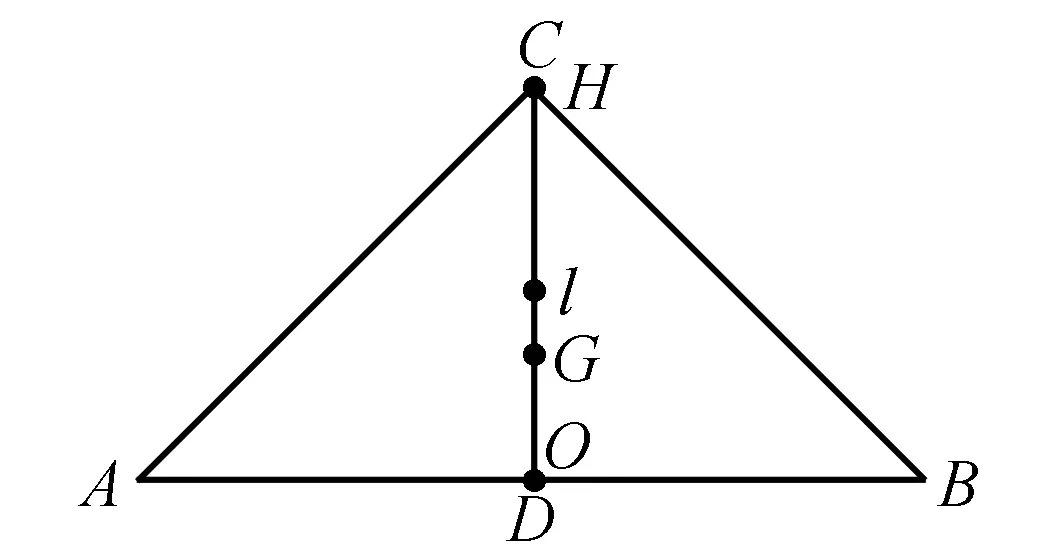
图1


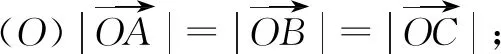

我们在解决向量问题当中提到的四心就是以上的这四种向量的关系,虽然常规来看内容还是蛮简单的,但是理解起来却有很大的难度,而且这类题目在短时间内肯定是搞不定的,所以我们在求解问题的过程中,一定要把题目特殊化,即要把题目当中给出的三角形特殊化,想象成等腰直角三角形,切记不要变成等边三角形,这是因为等边三角形四心合一,即重心、垂心、外心、内心四个心是同一个点.而等要直角三角形的四心就不是同一个心,但是这四心却都在一条高线上,如图1所示.正是由于很多的三角形都不满足这个关系,而只有在等腰直角三角形中,这四个心才能进行区分,而且这四个心都在高线CD上,这样一来题目就能够很快地得到解决.下面将具体以实际问题来给同学们呈现这种题目的分析过程和解题思路.
二、利用基本关系解决实际问题
审题的过程是非常关键的,同学们在解答问题的时候,应该按照一定的技巧来进行思考,这样更容易得出正确的答案.先看例题一:
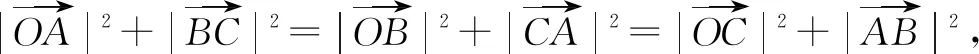
A.外心 B.垂心 C.内心 D.重心
分析在同学们拿到这道题目的时候,首先应该把这个三角形特殊成一个等腰直角三角形来对题目要求进行判断,接下来我们假设这个等腰直角三角形的腰长为2,则三角形的关系以及各边的长如图2所示.

图2
那么接下来我们试着做一种假设,如果A选项是正确的,那么题目中出现的点O就应该在D点的位置上,接下来我们试着把数值代入到题目中给出的关系当中来进行判断:
这样看来A选项是不正确的.也许有些同学不明白为什么这样判断,其实我们把题目内容赋予一个特殊值,如果特殊值不满足题目的某选项,那么就可以判断这个选项是不正确的.同学们接着按照这种思路来看B选项是否正确:

图3
若题目中的点O是三角形的垂心,那么点O应该在C点的位置上,如图3所示.继续对题目当中给出的关系代入特殊数值进行验证,可以得到
接下来我们再看例题二:

分析在这道题目的审题过程中,我们仍然采取相同的做法,先把这个等腰直角三角形画出来,然后把题目中给出的已知条件进行推导和转换,如图4所示.

图4


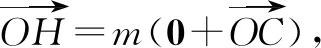

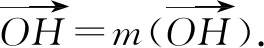
所以即可求得m=1.
虽然四心问题听起来很可怕,看起来公式也比较繁琐,但是如果同学们能够扎实的掌握,在平常的考试或练习当中一旦出现了这样的一种问题,同学们就能快速地运用公式或是各个“心”在等腰直角三角形当中的位置快速地解出问题的答案.
