基于图像识别的粉煤灰渗透率计算方法

何伟，任孟健，肖尧

（湖南大学 土木工程学院，湖南 长沙，410082）

粉煤灰是燃煤锅炉及电厂排放的一种工业废渣.由于其组织疏松，具有球形颗粒特征及良好的渗透性，因而被广泛应用于道路工程的路堤填筑[1].粉煤灰的渗透性能与路堤的压实度和稳定性等力学性能密切相关[2-3]，因而研究粉煤灰的渗透性能成为粉煤灰路基填筑的关键问题.国内外学者对粉煤灰渗透率做了一定的研究.如Bros 等[4]对灰坝的渗流控制进行研究，得出粉煤灰渗透系数的各向异性比值为2～6；陈愈炯等[5]对粉煤灰的物理、化学及力学性质作了初步研究，得出粉煤灰的渗透系数约为10-3～10-5cm/s；黄敬如[6]通过现场试坑注水试验，对粉煤灰坝体的渗透性能进行了初步探讨，测得粉煤灰坝体的渗透系数为（2～10）×10-4cm/s，并指出水平向渗透系数大于垂直向渗透系数.这些研究大多停留在试验阶段，对粉煤灰渗透率的理论研究还不够深入.赵明华等[7]基于分形理论推导了粉煤灰渗透率与孔隙分维数的关系式，评价了孔隙分维数对粉煤灰渗透率的影响.实际上，孔隙和颗粒在粉煤灰试件中是随机分布的，孔隙之间存在连通和不连通的情况，只有相互连通的孔隙才与试件的渗透率有关，因而，孔隙率并不是影响渗透率的最主要因素.Abbas[8]明确指出，试件的渗透性与孔隙率相关，渗透性高低取决于内部孔隙的连通状况.因此考虑粉煤灰孔隙的连通性的渗透率研究意义重大.然而，以往的研究中考虑粉煤灰孔隙的连通性对渗透性能影响的定量分析鲜有报道.

鉴于此，本文将首先采用显微数码成像技术获取粉煤灰试件孔隙和颗粒分布函数.然后，基于Matlab 编程，根据无放回摸球过程产生随机数，计算粉煤灰试件的孔隙连通率.在此基础上，推导得到粉煤灰渗透率的计算公式.最后，通过与其他文献结果的对比验证本文方法的正确性.

1 孔隙结构图像识别原理与方法

近年来，随着对岩土工程领域问题认识的不断深入，国内外学者开始将岩土工程领域中的问题向微观结构进行拓展，在这种趋势下图像识别技术及图像处理技术的应用得到了快速发展.在各类图像识别技术中，数码光学显微镜由于强大的图像区域选取、图像区域处理以及图像分析结果输出功能而得到了广泛应用.洪宝宁等[9]在对岩土工程材料的力学模型探究和本构关系分析中，引用了长距离显微镜，并通过数字图像处理软件的辅助，实现了图像识别、图像处理以及图像数据的输出，实现了对试验土样的孔隙率、孔隙面积、孔隙数目以及颗粒定向度等微观结构力学参数的分析.基于此，本文使用数字图像技术对粉煤灰微观结构的图像进行分析，在考虑孔隙连通影响条件下建立粉煤灰渗透率公式，其试样制备和图像采集方法如下.

1.1 试样的制备

首先，按最优含水率采用轻型击实的方法制作粉煤灰试样.采用内径为61.8 mm 的不锈钢薄壁取土器取样，经低温冷冻干燥后用锋利的小刀削去表层土，并用橡皮球吹去试件表面的扰动颗粒，使其暴露出新鲜的表面供研究.

1.2 图像采集

采用体式显微镜选取粉煤灰试件的4 个不同位置进行拍照，放大倍数为150 倍，图片大小为352×352（单位：像素），每1 个单位像素代表1.425 μm.将获得的4 张真彩色原始显微图像，利用专业图像处理软件进行去噪声、对比度增强、背景平滑等初步处理，使图像更加清晰，然后将其转换成灰度图像，再通过直方图均衡化、弱化等处理，使粉煤灰孔隙结构特征更加明显.采用目视法对图像进行阈值分割，形成二元图像，白色为固体颗粒，黑色为孔隙，图1 表示典型的图像处理过程.最后利用图像分析软件统计孔隙和颗粒的分布情况.

图1 粉煤灰试样的显微图像处理典型过程Fig.1 Typical process of microscope image processing on fly ash samples

2 确定孔隙颗粒分布函数

根据图像软件分析结果，不同尺寸的孔隙总数目为875，按照组距为9.5 μm 把孔隙分为12 个组，各组的孔隙累计数量和频率见表1，以孔隙直径为横坐标，以频率/组距为纵坐标的粉煤灰孔隙直径分布见图2.颗粒总数目为551，按照组距为12 μm，把颗粒分为14 个组，各组的颗粒累计数量和频率见表2，粉煤灰颗粒直径分布见图3.

表1 粉煤灰试件孔隙分布Tab.1 Pore distribution of fly ash specimen

图2 粉煤灰孔隙直径分布Fig.2 Pore diameter distribution of fly ash

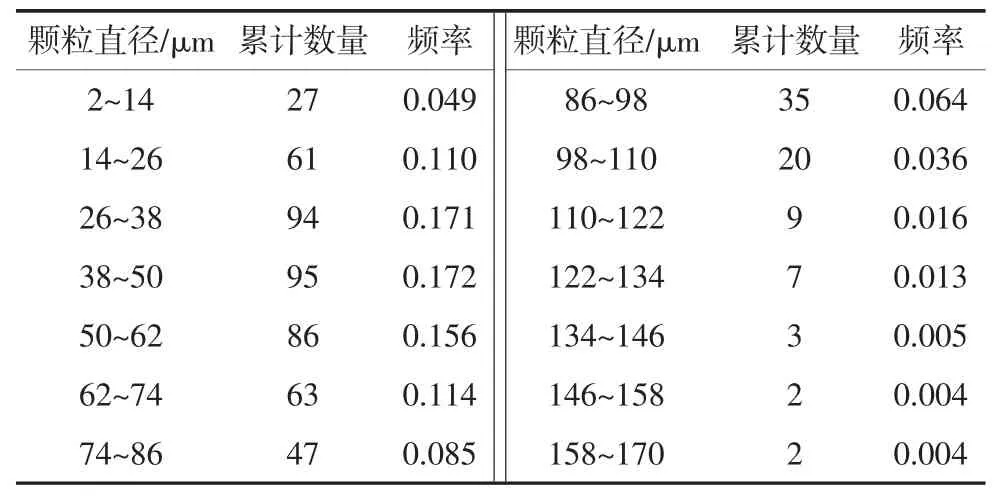
表2 粉煤灰试件颗粒分布Tab.2 Particle distribution of fly ash specimen

图3 粉煤灰颗粒直径分布Fig.3 Particle diameter distribution of fly ash

从图2 可看出，粉煤灰孔隙分布符合指数分布.

通过非线性最小二乘拟合，确定指数分布参数λ=0.054，μ=1.677.粉煤灰颗粒分布符合瑞利分布：

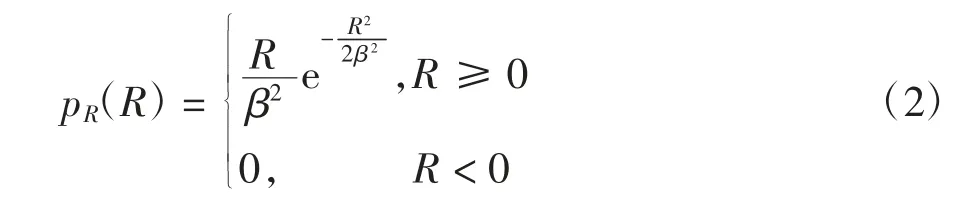
通过非线性最小二乘拟合，确定瑞利分布参数β=41.5.

3 粉煤灰孔隙连通系数的确定

粉煤灰孔隙连通情况与不同尺寸的孔隙和颗粒的排列密切相关.根据图像分析软件得到的孔隙和颗粒的分布，按照吴恩江等[10]对孔隙大小的分级标准，将孔隙和颗粒分为3 个等级.

1）微孔隙：孔径在1～10 μm 之间，在较高压力下水可渗流，但渗透率较低.

2）小孔隙：孔径在10～100 μm 之间，在自然状态下，有一定的水头压力时，水可以通过其渗流，渗透性较好.

3）大孔隙：孔径大于100 μm，地下水可以在其内较顺畅地渗流.

每个等级的孔隙和颗粒的特征粒径为：

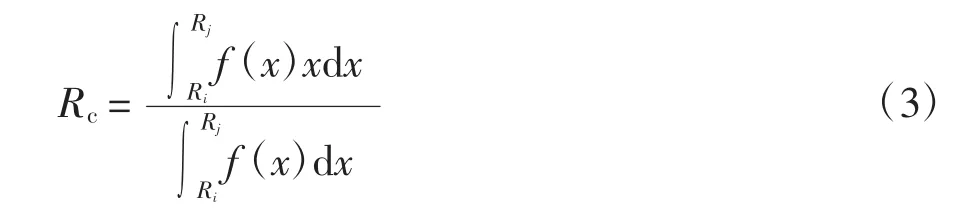
式中：f（x）为密度函数，对于孔隙采用式（1），颗粒采用式（2）；Ri和Rj分别为该等级粉煤灰孔隙和颗粒直径的最小值和最大值.各等级孔隙和颗粒的特征粒径和数量见表3.

将孔隙和颗粒按特征粒径从小到大的顺序编为1～6 号.为了更好地模拟孔隙和颗粒随机分布的情况，按照孔隙和颗粒的相对比例，把各个特征粒径的孔隙和颗粒数量按表3 扩大10 倍，按编号1～6 的顺序依次排列.基于无放回摸球过程采用Matlab 编程，产生随机数，随机数的产生流程见图4.在5 倍的最大颗粒特征粒径的方格网中按照产生的随机数顺序依次排列孔隙和颗粒.孔隙和颗粒的排列见图5.

图4 模拟无放回摸球过程产生随机数流程图Fig.4 Flow chart of generating random number

图5 粉煤灰孔隙和颗粒分布图Fig.5 Distribution plan of pores and particle

图6 粉煤灰连通孔隙分布图Fig.6 Distribution plan of connected pores of fly ash

定义连通系数Cf为：

按照图6，粉煤灰的连通系数为0.55.

4 粉煤灰渗透率公式推导

假设有一根长为L，内径为R 的毛细管，其流体黏度为μ，在压力差（P1-P2）下作层流流动，单根毛细管中的渗流流量为[11-12]：

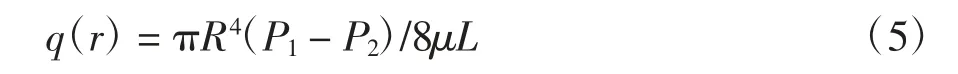
通过某个单元截面A 的总流量Q 为：

式中：R1和R2分别为最小和最大孔隙半径.

根据Darcy 定律，可得粉煤灰渗透率为：

考虑孔隙连通系数Cf的粉煤灰渗透率为：

5 讨论

由于本文中粉煤灰试件制作方法和数码体式显微镜的分辨率与文献[7]一致，因此两者得出的渗透率结果具有可比性.本文中数码体式显微镜所能识别的最小孔隙半径R1为0.8 μm，研究区域面积A=2 486 402 μm2.最大孔隙半径R2按40～100 μm 取值，计算结果见表4.从表4 可看出，文献[7]和本文得出的渗透率结果在一个数量级，且结果十分接近.将本文渗透率计算结果和文献[7]的结果进行对比，如图7 所示.

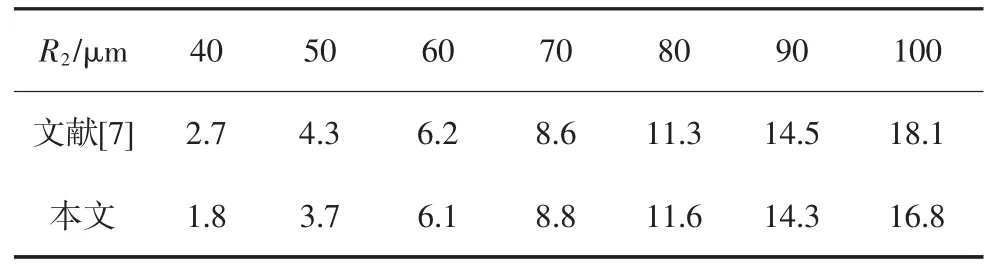
表4 文献[7]和本文的渗透率结果比较Table 4 Comparison of permeability result between reference[7]and this paper 10-2 μm2

图7 本文和文献[7]渗透率结果对比图Fig.7 Comparison of permeability results between this paper and reference[7]

由图7 可知，基于分形理论的渗透率计算结果同本文使用的基于粉煤灰孔隙连通率公式计算结果十分接近，图中甚至存在部分数据点重合，且渗透率同最大孔隙半径之间的变化趋势一致，均随着最大孔隙半径的增大而不断增大.这也从另一个角度对本文公式的有效性进行了充分的印证.

6 结论

本文通过图像识别技术得到了粉煤灰试件的孔隙分布和颗粒分布规律，基于无放回摸球过程，采用Matlab 编程模拟孔隙和颗粒在5 倍最大颗粒当量圆直径方格中的随机排列，得出了孔隙的连通率，并在此基础上建立了粉煤灰渗透率公式，将渗透率的计算公式变量缩减为3 个，极大地简化了渗透率的计算.本文使用的基于粉煤灰内部结构孔隙连通率的计算公式计算结果与基于分形理论下粉煤灰渗透率的计算结果非常接近，吻合度高，变化趋势相一致，粉煤灰的渗透率随着最大孔径的增加而逐渐增大.