晶体硅太阳电池应力的理论分析

（湖南大学 土木工程学院，湖南长沙 410082）

光伏组件上的荷载主要是风荷载.采用层压工艺制造的多层结构光伏组件，晶体硅电池片是离散的内埋于EVA 胶层中，这种内埋形式一是给电池片的应变测量带来不便，二是给电池片的应力分析计算带来困难.另一方面，EVA 胶属于粘弹性材料，其储能剪切刚度与温度密切相关[1]，在低温时剪切刚度大幅升高，从而引起电池片的应力增加.我国地域辽阔，冬季南北温差很大，而现有的规范并未针对应用区域对组件的结构形式作出相关指引，因此在冬季严寒地区应用光伏系统时，由于风压而导致组件电池片出现隐裂和碎片等，使其经济效益大幅低于预期.

目前针对光伏组件的相关研究工作较少，主要集中在以下几个方面：1）外荷载（如风载等）作用时组件整体的强度研究[2，3]；2）硅电池片在荷载作用下的机械强度及破坏特征[4-7]；3）基于有限元法的电池片应力分析，以有限元方法研究组件在热循环作用下[8-11]及在荷载作用下[12]各层的应力和应变.由于上述研究将电池层作为一连续夹层处理，与实际离散排列的、片间无相互作用的电池层不符.

对于内埋于EVA 胶层的电池片，组件面板玻璃的变形将导致EVA 胶层产生剪应变并将荷载传递至电池片.文献[13]基于最小势能原理导出了光伏组件晶体硅电池片的位移场及应力场，由于位移分量取为重三角级数形式，其计算结果在电池片边缘处的Von Mises 等效应力为零.文献[14]基于Ansys 分析了组件电池片的应力分布，表明处于双向拉伸状态的电池片边缘处的Von Mises 等效应力不为零.对于晶体硅电池片应力的正确描述目前尚无相应的理论解.

本文针对光伏组件晶体硅电池片的受力特点导出了光伏组件晶体硅电池片应力场和位移场的级数解，计算了组件在不同风压及EVA 胶膜弹性模量发生变化时晶体硅电池片的应力分布.计算结果与文献[14]的有限元结果进行了比较，验证了理论解的正确性，并对广泛应用的125 mm×125 mm 和156 mm×156 mm 两种主流电池片进行了讨论.本文的理论解对光伏组件在不同风荷载及环境温度下晶体硅电池片的应力分析提出了理论计算方法，为光伏工程设计提供了依据.

1 电池片理论分析简化模型

图1 为目前分体式光伏组件的主流构造形式，依次为3.2 mm 超白钢化玻璃面板、0.5 mm 的EVA胶膜、0.19 mm 的晶体硅电池片、0.5 mm 的EVA 胶膜、0.35 mm 的TPT 背膜，经层压后形成的多层组合结构.电池片则离散地分布于EVA 胶层中，片与片的间距约1～2 mm，之间仅有两条宽约3 mm，厚约0.1 mm 的金属片作为电气连接，因此电池层可看成一离散的、片与片之间无相互作用的薄层.组件受外荷载作用而弯曲变形时，EVA 胶层发生剪切变形，将荷载传递至电池片表面，在电池片内产生应力.

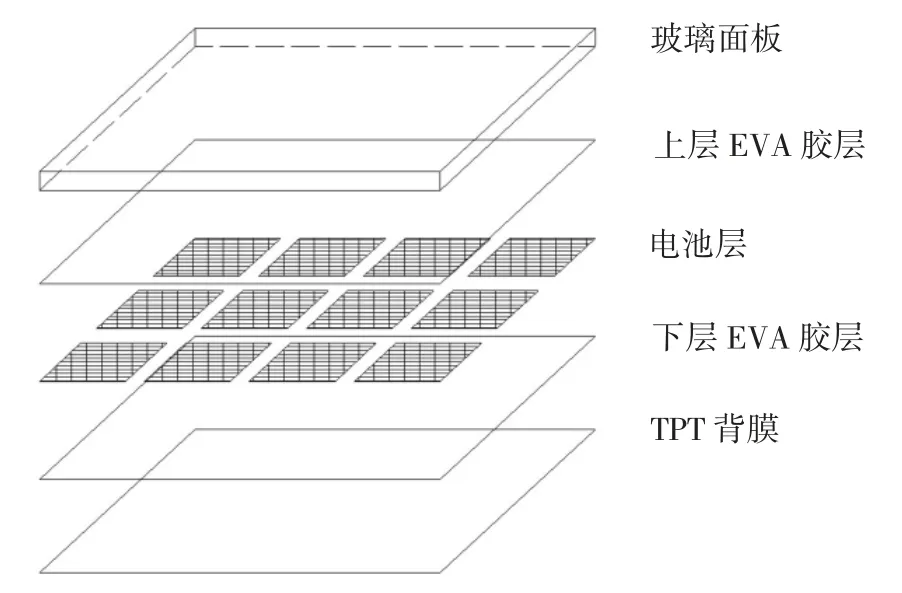
图1 组件的多层构造形式Fig.1 Laminated configuration of photovoltaic module

考虑电池片的受力情况，本文的理论分析基于以下的简化模型：

1）垂直于电池片表面的正应力σz与电池片的面内应力分量相比很小，可忽略；

2）组件弯曲时，电池片表面的荷载来自于上下表面EVA 胶膜的剪应变，而EVA 胶膜的剪应变则由面板玻璃及TPT 背膜与电池片的变形差异引起.TPT 背膜是厚度约0.35 mm 的聚氟乙烯复合膜，弹性模量比硅电池片低约2 个数量级，其变形在电池片范围内将受到电池片的约束，因此忽略TPT 背膜对电池片下表面的作用；

3）忽略EVA 胶对电池片端面沿厚度方向的作用；

4）电池片的厚度仅为0.19 mm，可以看成一偏离组件中性面的离散薄层，组件弯曲时电池片处于整体双向受拉和弯曲的组合作用，其中弯曲应力是次要的，因此以下的分析忽略电池片的附加弯曲应力，认为面内应力沿厚度方向不变；

5）组件的面板玻璃尺寸一般比电池片的尺寸大一个数量级，因此近似认为面板玻璃下表面的应变在电池片范围内为常数.

取图2 所示的坐标系，基于上述的简化模型及对称性可给出如下的应力边界条件和对称关系：

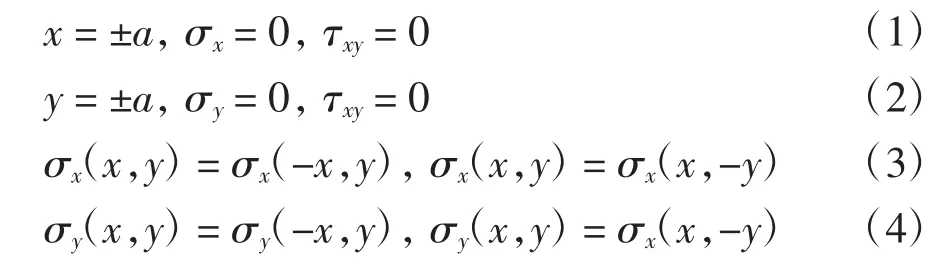
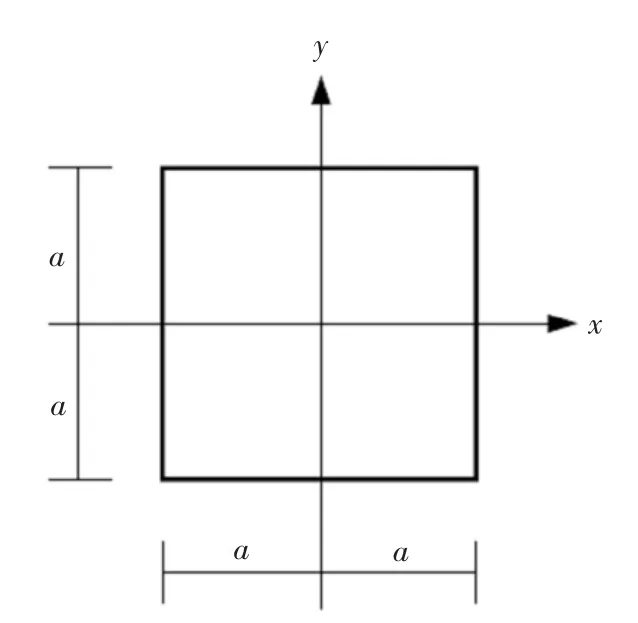
图2 电池片及坐标系Fig.2 The cell and coordinate system

2 电池片的应力场和位移场

图3 所示为按简化2）和3）由组件中取出仅包含一片电池的层合板计算单元沿x 方向的变形示意图，与电池片相对应的面板玻璃底面在x 方向的正应变值为.组件发生弯曲变形时，电池片上表面由于受到EVA 胶的剪应力作用在x 方向产生位移ux.不考虑在变形过程中EVA 胶层的厚度变化，且在小变形时认为EVA 胶的应力应变近似服从线性关系，则任一点x 处EVA 胶层的剪切应变为

式中：δ 为组件的弯曲中面至面板玻璃底面的距离；b为EVA 胶层的厚度.

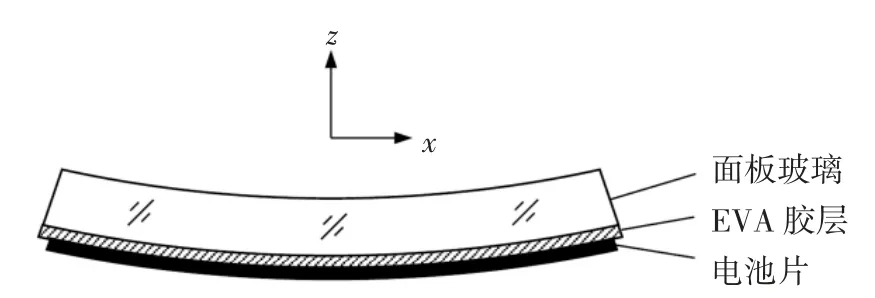
图3 组件计算单元Fig.3 The calculation unit of the module

作用于电池片上表面沿x 轴方向的分布面荷载px可表示为

式中：GEVA为EVA 胶的储能剪切刚度.同理，沿y 方向的分布面荷载py可表示为

考虑一长度和宽度分别为dx 和dy、厚度为t（电池片厚度）的电池片单元体如图4 所示，根据简化4），忽略电池片的附加弯曲应力，认为电池片的应力沿厚度方向不变.则不考虑体力时单元体沿x 和y方向的平衡方程为

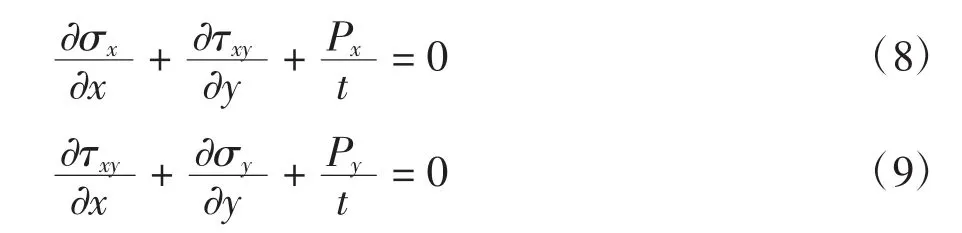
相容方程

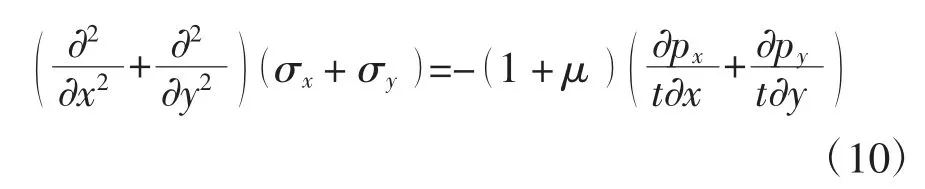
式中：μ 为电池片的泊松比.

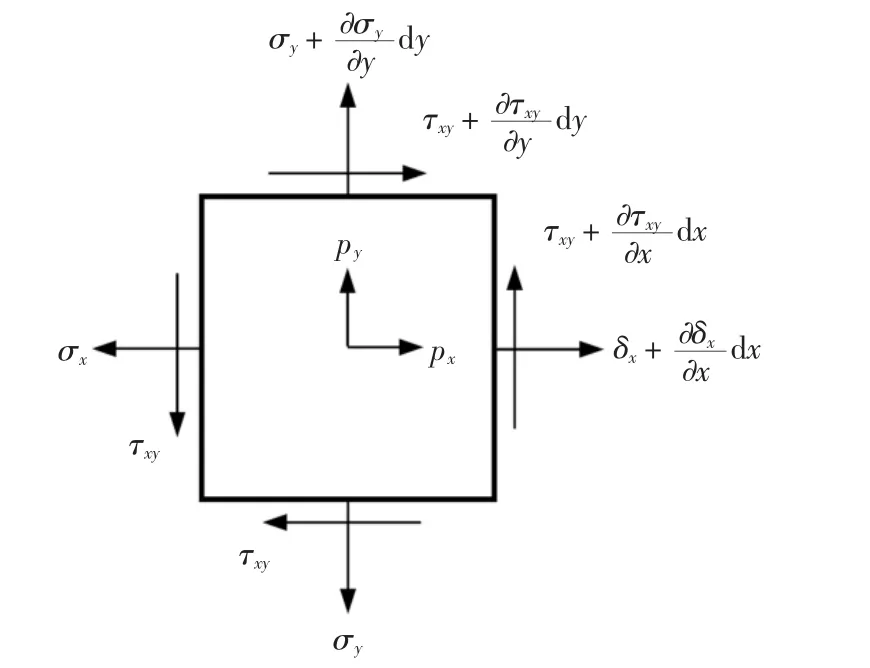
图4 电池片单元体及应力Fig.4 The cell unit and the stresses

式（8）、（9）分别对x 和y 求导并消去剪应力分量τxy，得到

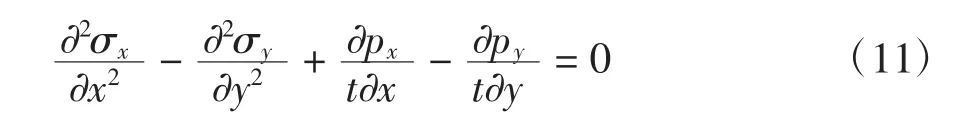
式（6）、（7）代入式（10）和（11），并利用几何方程和物理方程消去位移分量ux、uy，得到

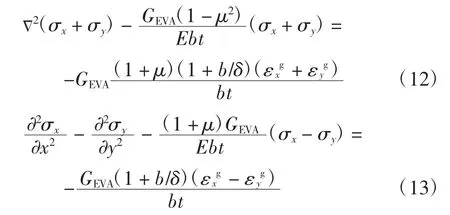
式中：E 为电池片的杨氏模量.

考虑边界条件（1）～（4），由分离变量法得到式（12）的解为

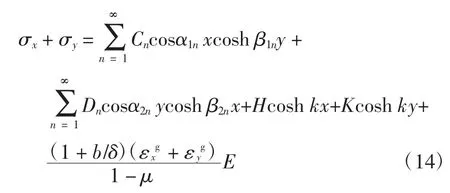
式中：Cn、Dn、H、K 为待定系数，且

式（14）与式（13）联立解出应力σx和σy的一般表达式为

式中，Ln、Mn为待定系数，且

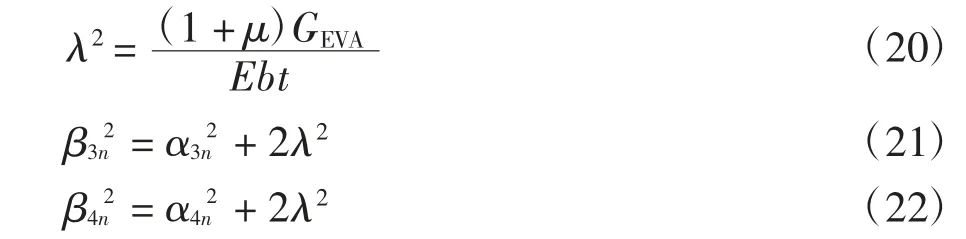
得到σx和σy后，再结合物理方程和几何方程及式（6）（9）求解τxy，此处不再叙述.应力分量需满足应力边界条件（1）～（4），则有

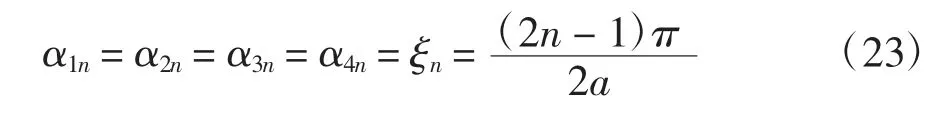
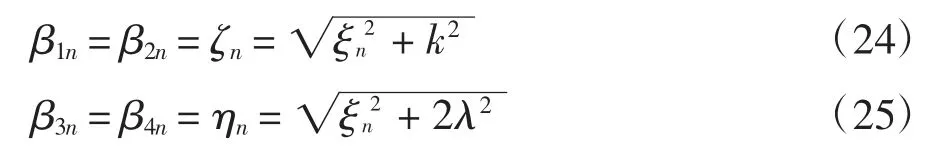
由应力边界条件确定待定系数，并将各系数与常数进行适当合并，以Pn、Qn、Rn、Sn表示，得到电池片的应力场和位移场如下

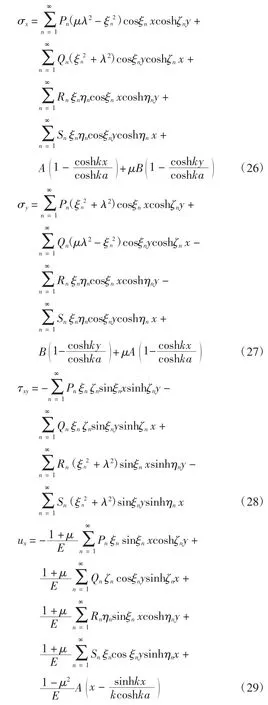
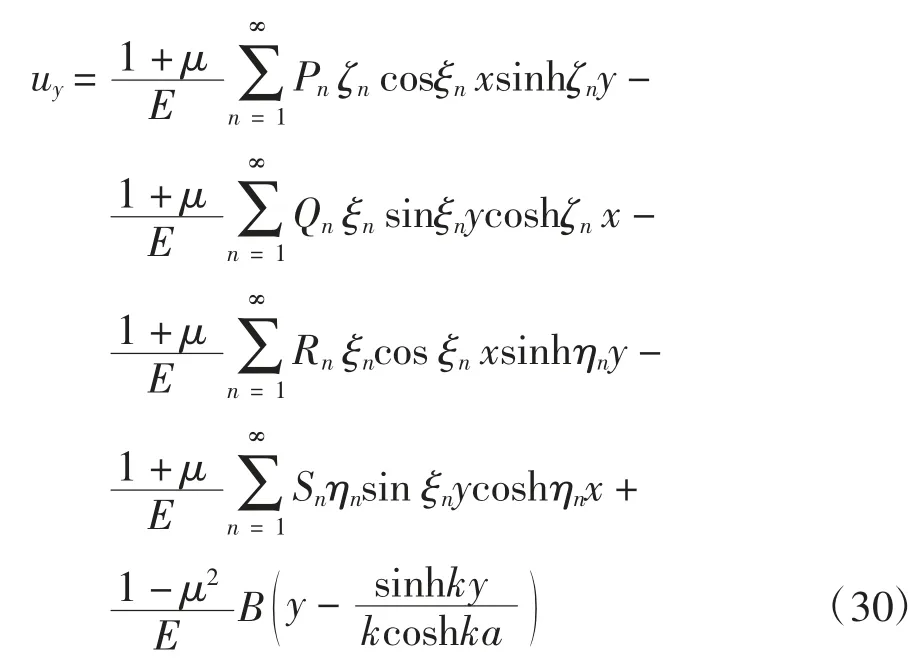
式中：

该级数解收敛较快，取6～8 项即可得到较精确的结果.

3 算例及结果

3.1 与有限元结果比较

文献[14]基于Ansys 对面板尺寸为1 580 mm ×808 mm 的195 W 单晶硅标准组件在风荷载作用下组件中点处晶体硅电池片的应力进行了计算和分析，考虑了不同风压及EVA 剪切模量变化对应力的影响，本文结果与文献[14]的有限元结果进行比较.以本文的解答对面板尺寸为1 580 mm×808 mm 的195 W 单晶硅标准组件进行了相同计算，该组件坐标系取为x 轴沿组件短边方向，y 轴沿组件长边方向，组件在风压标准值分别为0.50、0.65、0.80、0.95、1.10 kN/m2时面板玻璃中点处下表面的应变值εxg、εyg如表1 所示[13].

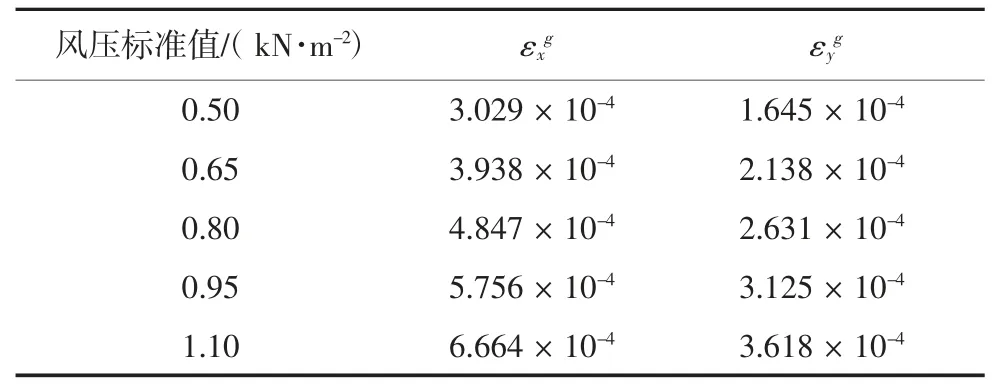
表1 组件面板玻璃中点处的应变值Tab.1 The normal strains at the middle of the panel

处于双向拉伸状态的电池片，以Von Mises 等效应力σeq来衡量电池片内一点处的应力

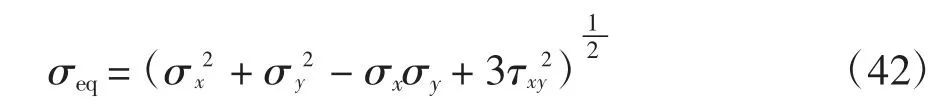
光伏组件的EVA 胶属于粘弹性材料，其储能剪切刚度随温度的变化较大.研究表明[1]，在60 ℃时的GEVA约为3 MPa.而温度降低至-20 ℃时则大幅增加至约40 MPa.因此计算电池片应力时应考虑GEVA的变化.

以本文理论模型计算了上述组件在风压为0.65 kN/m2作用下，EVA 胶膜的储能刚度GEVA=10 MPa时电池片Von Mises 等效应力沿x 轴和y 轴的变化如图5 所示，并与文献[14]的相应结果进行比较.电池片的各计算参数取为：E=180 GPa，μ=0.27，a=62.5 mm，t=0.19 mm，b=0.5 mm.

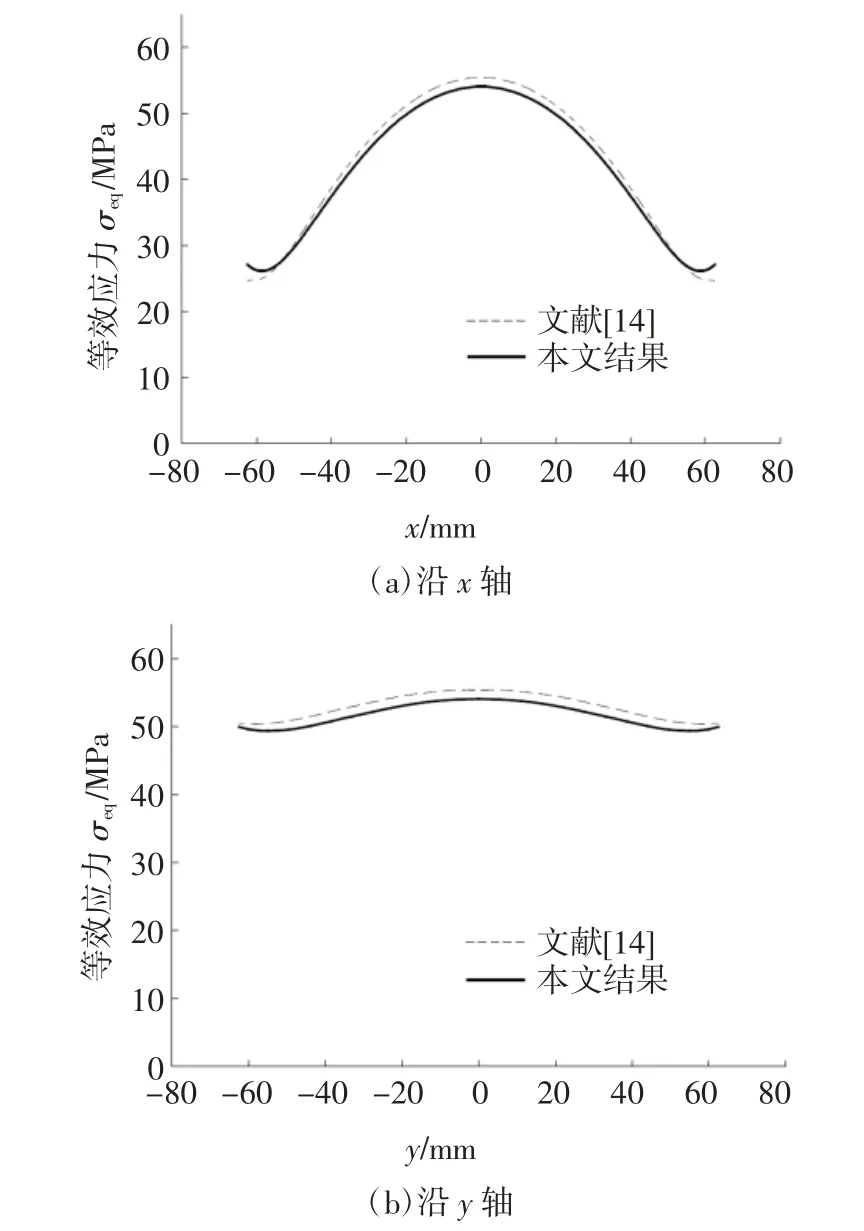
图5 电池片的Von Mises 等效应力的比较Fig.5 The variation of the Von Mises stress in cell

在组件的工作温度范围内，EVA 胶所呈现的弹性模量比玻璃的弹性模量（72 GPa）低约3 个数量级，而电池片是离散地分布于EVA 胶层中.有限元结果表明，EVA 胶层、TPT 背板和电池的组合层对组件的整体刚度影响很小，组件弯曲时近似以面板玻璃的中性面弯曲变形[14]，因此计算时组件的弯曲中面至面板玻璃底面的距离δ 取为1.6 mm.

图5 的结果表明：1）最大应力均出现在电池片中点，与有限元结果比较，本文理论结果的最大应力值偏低约2.51%；2）沿x 轴方向的应力在边界处本文结果略高于有限元结果，而沿y 轴方向则始终低于有限元结果.电池片应力沿x 轴的变化较大，而沿y 轴的变化较小.

当EVA 胶剪切模量GEVA由2 MPa 变化至40 MPa，组件面板风压值分别为0.50、0.65、0.80、0.95、1.10 kN/m2时，以本文理论模型计算的电池片中点处最大等效应力如图6 所示，文献[14]的结果也列于图中进行比较.由图6 可以看出，二者的结果符合较好，但本文的结果始终低于有限元结果，其原因是本文的理论模型忽略了TPT 背膜对电池片的影响.

图6 电池片最大等效应力随GEVA 的变化Fig.6 The variation of the maximum Von Mises stress in cell with increasing GEVA

3.2 电池片尺寸的影响

随着晶体硅技术的发展，156 mm×156 mm 的大尺寸晶体硅电池片已在光伏组件中得到广泛应用.目前的156 mm×156 mm 电池片组件仍采用3.2 mm 面板玻璃，在相同风压下电池硅片的应力将有所提高.

以本文理论模型计算的两种规格电池片组件在组件尺寸及各计算参量相同的情况下，风压值为0.65 kN/m2时电池片中点处等效应力随EVA 胶层剪切模量GEVA的变化如图7 所示.结果表明，电池片尺寸的增加将引起应力较大幅度的上升，从而电池片破裂的隐患增加.因此，采用大尺寸电池片的组件应适当增加面板玻璃厚度，提高组件的整体弯曲刚度，可有效降低电池片的应力.

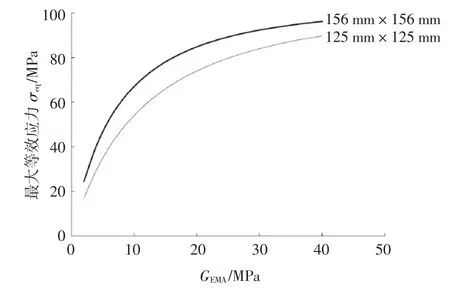
图7 两种电池片组件的最大应力比较Fig.7 The comparison of the maximum stress in two kinds of cells

4 结论

1）针对光伏组件晶体硅电池片的受力特点导出了晶体硅电池片应力场和位移场的级数解答.对尺寸为1 580 mm×808 mm 的195 W 单晶硅组件面板中心处电池片的应力进行了计算并与文献[14]基于Ansys 的有限元结果进行了比较.结果表明二者符合很好.

2）比较了125 mm×125 mm 和156 mm×156 mm 两种规格电池片组件在风压为0.65 kN/m2时的应力，结果表明电池片尺寸的增加将导致应力的增大.因此在光伏系统设计时应充分考虑当地的气象数据，并结合应力分析计算，选用合理的组件.

3）现行光伏规范中并未考虑EVA 胶层储能剪切刚度随环境温度的降低而增大，从而引起电池片应力的升高.这种对安装地区不加区分的应用，导致在冬季严寒地区安装的光伏系统其电池片由于高应力而出现性能过早衰退.因此在相关规范的修订中建议将环境因素（温度、风压）纳入指引.