改进频率相关黏性阻尼模型的时程计算方法
2020-10-11孙攀旭杨红赵雯桐刘庆林
孙攀旭,杨红,赵雯桐,刘庆林
(1.重庆大学 土木工程学院,重庆 400045;2.重庆大学山地城镇建设与新技术教育部重点实验室,重庆 400045;3.深圳信息职业技术学院 交通与环境学院,深圳 518172)
目前应用最为广泛的阻尼模型是黏性阻尼模型,黏性阻尼模型由于其数学处理上的简易性,在结构动力计算中得到了广泛应用,但其存在每周期耗散能量与外激励频率相关的特点[1-4],这与大部分材料在实验中每周期耗散能量与外频率无关的现象不一致[5].
能够更真实地描述实验现象的复阻尼模型具有体系每周期耗散能量与外激励频率无关的优点[6],但其自由振动运动方程的通解中存在发散项,造成复阻尼模型时程迭代计算结果不收敛[7].潘玉华等[8]提出了复阻尼运动方程的高斯精细积分法,吴泽玉等[9]提出了复阻尼运动方程的增维精细积分法,Yuan等[10]提出了复阻尼模型的迭代更新法,但上述方法均无法避免复阻尼模型的时域发散现象.针对复阻尼模型的缺陷,周正华等[11]依据线弹性体的时域本构关系,采用最小二乘法使其近似等于频域内的复阻尼本构关系,得到一种时域复阻尼本构方程,但该方程仅适用于给定的频率范围,且用于多自由体系计算时,其误差有待进一步分析.Reggio 等[12]采用Maxwell-Wiechert 本构模型,在频域范围内近似等效于复阻尼本构模型,得到在时域内稳定收敛的运动方程,但计算过程过于复杂.Wang[13]在频域内采用Rayleigh 阻尼矩阵等效复阻尼矩阵,进而避免发散现象,但存在计算结果不唯一、合理性不易判定的缺点.
假定阻尼力与结构体系的位移成正比,且与速度的方向相反,可进一步得到迟滞阻尼模型[14,15].迟滞阻尼模型保留了耗散能量与外激励频率无关的优点,同时时域计算结果稳定收敛,但其对应的阻尼体系在线弹性阶段具有非线性的缺陷[16,17].
如何解决上述阻尼模型的缺点,是提高结构动力计算结果可靠性的难点之一.针对复阻尼模型,本文采用频域转化原则得到频率相关黏性阻尼模型,同时基于加速度与位移的关系假定,进一步将其改进为适用于迭代计算的改进频率相关黏性阻尼模型.在此基础上,结合常平均加速度法和模态叠加法,提出了基于改进频率相关黏性阻尼模型的多自由度体系时程计算方法.
1 基于加速度与位移关系的改进频率相关黏性阻尼模型
1.1 运动方程的构建
单自由度体系的复阻尼运动方程为
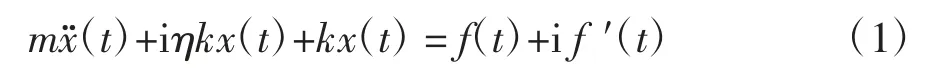
式中:m 为体系的质量,k 为体系的刚度,η 为损耗因子,t 为虚数单位,i=,f(t)为外激励荷载,f(t)通过复化对偶原则[18]得到f ′(t).
将方程(1)进行傅里叶变换,可得
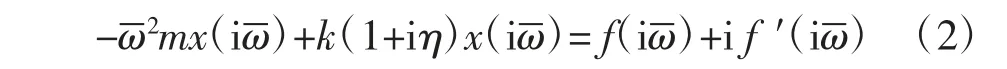
因位移响应的振动频率不为零,方程(2)可转化为
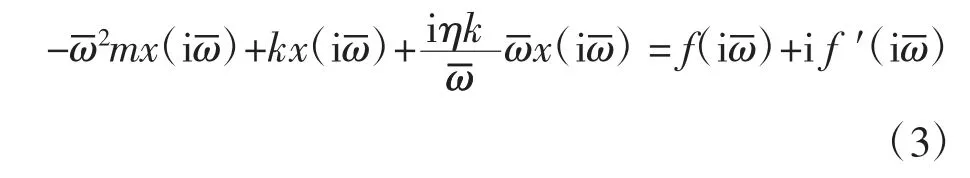
对方程(3)进行傅里叶逆变换,可得到结构的频率相关黏性阻尼运动方程为
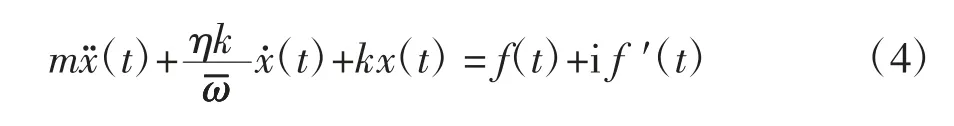
在实数域计算时,方程(4)右边的虚部激励可不考虑,方程(4)进一步转化为

方程(5)中结构的振动频率是未知项,导致频率相关黏性阻尼模型无法直接进行结构动力响应的时程计算.
设单自由度体系在激励频率为θ 的谐波作用下,体系处于稳态反应时,位移响应为
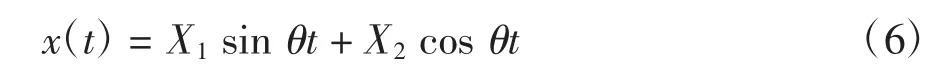
由式(6)可得到加速度响应为
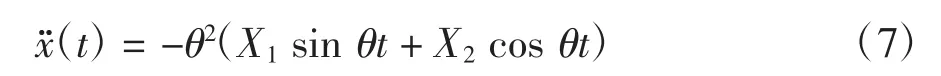
由式(6)和式(7)可得

因此,假定结构位移响应的振动频率可由位移和加速度得到,即

频率相关黏性阻尼运动方程进一步转变为
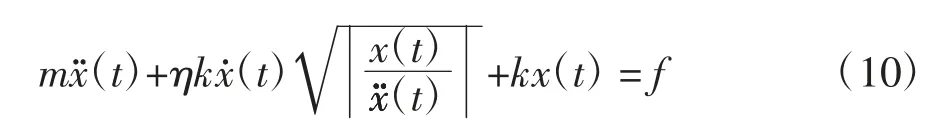
方程(10)为改进频率相关黏性阻尼模型的时域运动方程.
1.2 不同阻尼模型的对比分析
迟滞阻尼模型[14,15](以下称PVS)可克服复阻尼模型的时域发散现象,其阻尼力为

阻尼力在一个周期内消耗的能量为

由式(12)可知,PVS 具有阻尼力每周期耗散的能量与外激励频率无关的优点,但稳态反应时一个周期内阻尼力做功与实际耗散能量不相等,PVS 存在阻尼力消耗能量与实际耗散能量不符的缺陷.
改进频率相关黏性阻尼模型(以下称PVJ)下,由方程(10)可得阻尼力为

阻尼力在一个周期内消耗的能量为
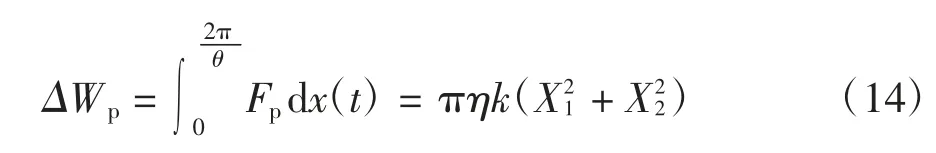
由式(14)可知,PVJ 在稳态反应时,阻尼力每周期耗散的能量与外激励频率无关,且一个周期内阻尼力消耗能量与实际耗散能量相等.因此PVJ 可有效克服PVS 阻尼力消耗能量与实际耗散能量不符的缺陷.
当结构处于简谐振动时,其位移响应如式(6)所示,可计算出两种阻尼模型下阻尼力与位移响应的变化关系如图1 所示.PVS 中阻尼力与位移的关系呈现非连续变化(图1(a)),结构体系具有非线性特点;PVJ 中阻尼力随位移连续变化(图1(b)),结构体系具有线性特点.线弹性状态下,单一振动频率的单自由度结构具有线性特征[19],但仅PVJ 呈现出线性特点,PVS 则存在理论误差.
综上,PVJ 不仅克服了PVS 中阻尼力消耗能量与实际不符的缺陷,还保证了单一振动频率下单自由度结构的线性特征.
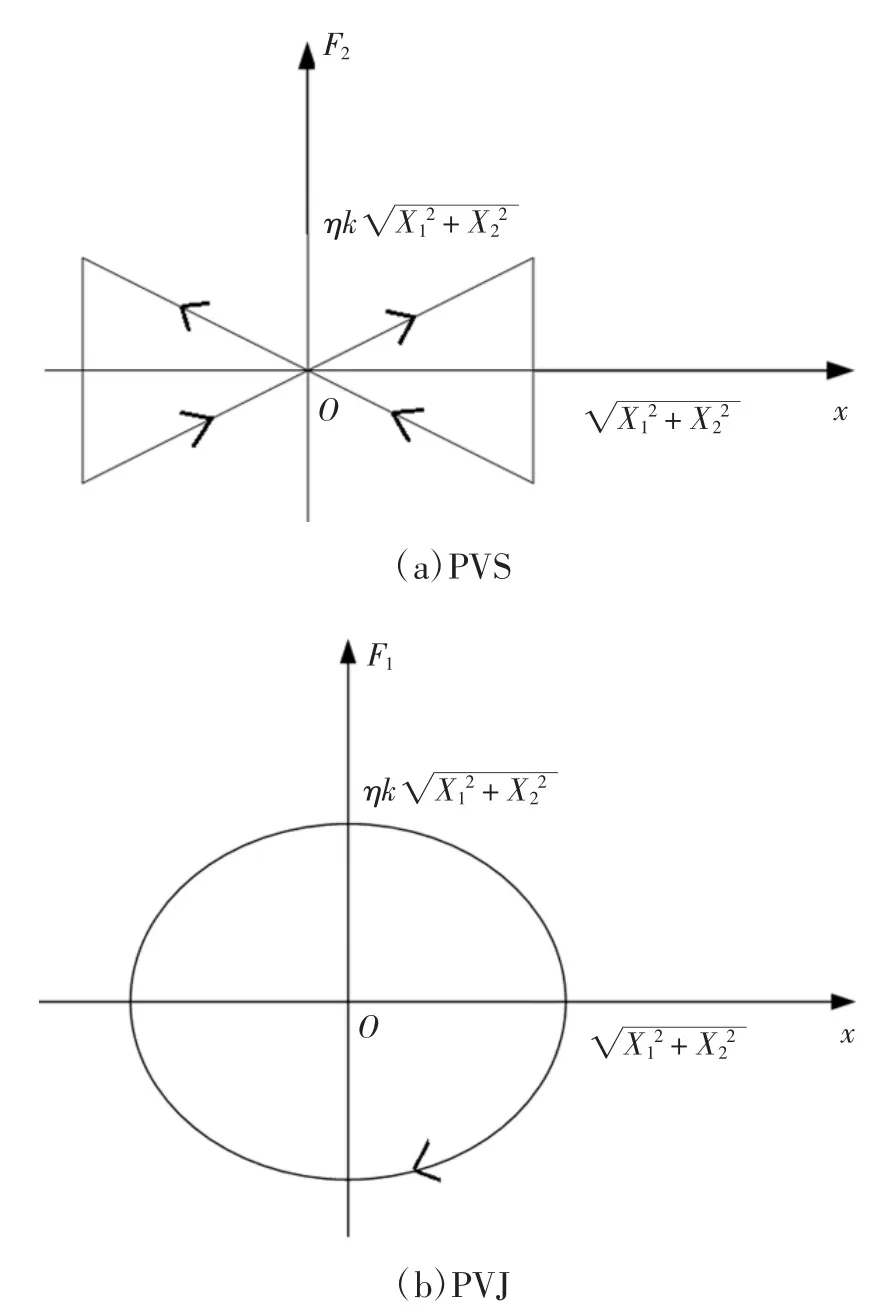
图1 阻尼力-位移关系曲线Fig.1 The damping force-displacement curves
2 基于改进频率相关黏性阻尼模型的时程计算方法
2.1 单自由度体系的时程计算方法
按照时间步长Δt 对时间进行离散,任意时刻可表示为tk=kΔt(k=0,1,2…).时间步长较小时,假定tk时刻到tk+1时刻体系振动为简谐振动,位移响应为
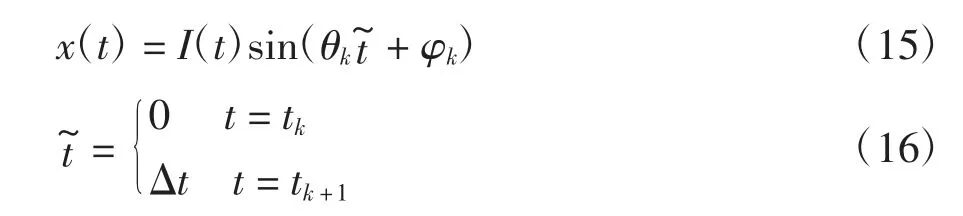
式中:I(t)为瞬时振幅,θk为tk时刻到tk+1时刻的瞬时频率,φk为tk时刻的瞬时相位.
2.1.1 单自由度体系运动方程初值
假定初始时刻t0时,体系的振动频率为有阻尼自由振动频率,初值的确定需要首先计算结构的有阻尼自由振动频率.
频率相关黏性阻尼模型下单自由度体系运动方程对应的特征方程为

求解方程(17),可得

由式(18)可知,特征根的虚部即为单自由度体系体系有阻尼自由振动频率,与体系的振动频率相等,得

进而得到有阻尼自由振动频率为

初值满足方程
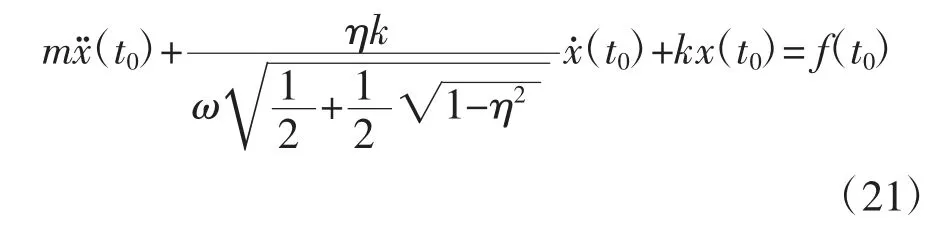
将x(t0)和代入方程(21)可得到.
2.1.2 基于常平均加速度法的时程计算方法
tk时刻到tk+1时刻的瞬时频率为

依据式(22),PVJ 运动方程可进一步转化为
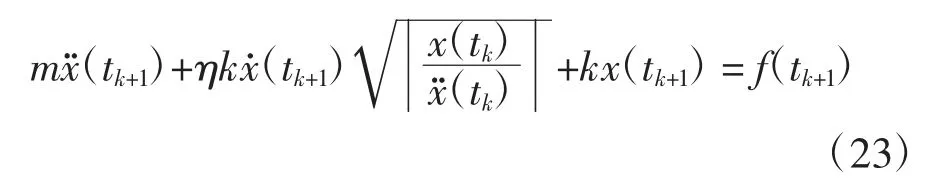
采用常平均加速度法,tk+1时刻结构的速度和位移为[20]
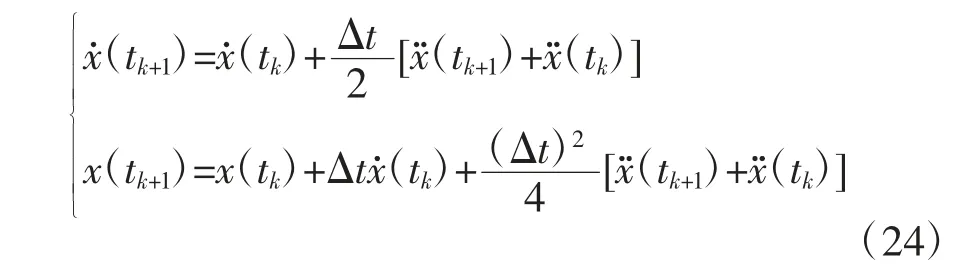
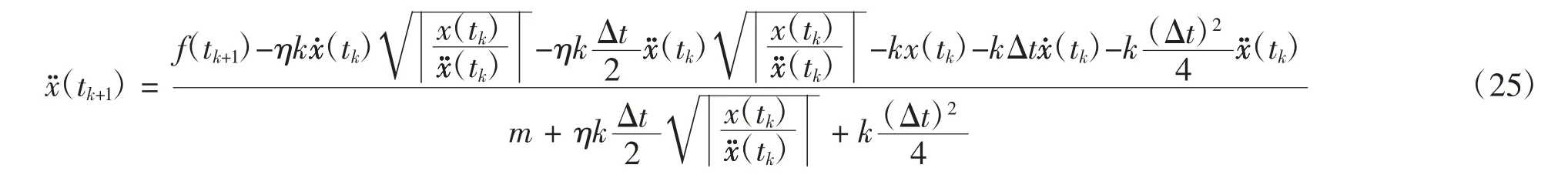
将式(24)代入方程(23)可得式(25).
x(tk)、代入式(25),可得到,进一步可由式(24)得到x(tk+1)和,据此即可完成PVJ 运动方程的时域迭代计算.
2.2 多自由度体系的时程计算方法
2.2.1 基于模态叠加法的时程计算方法
多自由度体系的PVJ 运动方程为
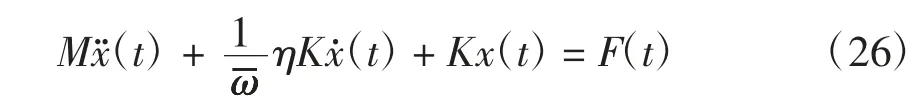
式中:M 为体系的质量矩阵,K 为体系的刚度矩阵,F(t)为外激励矩阵
对于单一材料体系,ηK 为比例矩阵,满足经典阻尼条件,方程(26)可直接采用模态叠加法[21]进行计算.
由质量矩阵、刚度矩阵得到多自由度体系的振型向量,可组装成振型矩阵
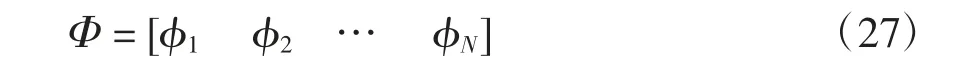
式中:φn(n=1,2,…,N)为第n 阶振型向量.
x(t)可由振型向量线性组合表示,即

多自由度体系的PVJ 运动方程则改写为

其中:

依据单自由度体系的时程计算方法,由方程(29)计算得到y(nt)、,然后由式(28)可得x(t)、,进而实现基于PVJ 的多自由度体系时程计算方法.
2.2.2 多自由度体系运动方程初值的确定
方程(29)对应的特征方程为

求解方程(31),可得
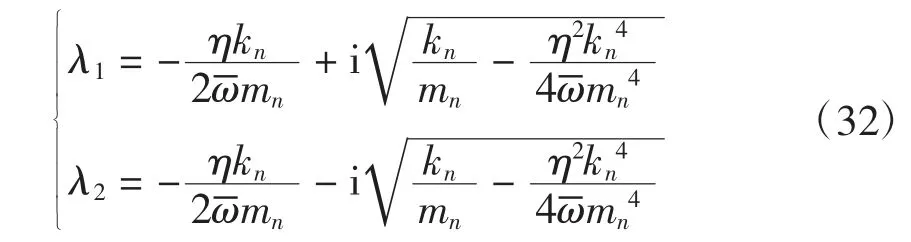
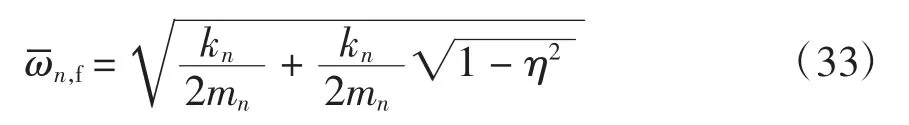
式(33)确定的振动频率可作为结构的初始振动频率,进而确定时程分析的初值,即
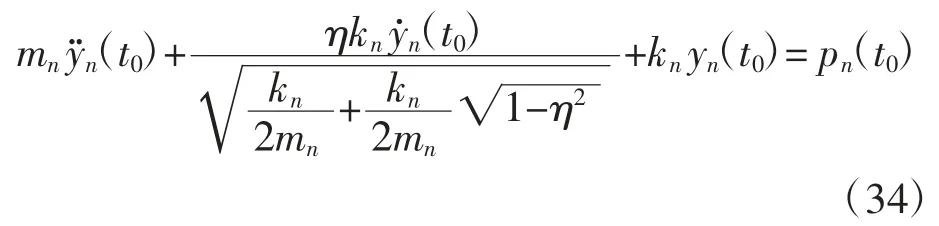
依据式(28),可由x(t0)和得到yn(t0)和,代入方程(34)可得到,从而完成初值的确定.
3 算例分析
3.1 单自由度体系
由式(18)可知,频率相关黏性阻尼运动方程两个特征根的实部均为负实数,因此其通解中仅含衰减项,而没有发散项,自由振动过程将是稳定收敛的.
以质量为1 000 kg,刚度为16 000 N/m,损耗因子为0.1 的单自由体系为例,其初始位移为5 cm,初始速度为8 cm/s,采用PVJ 计算体系的自由振动响应,所得结果如图2 所示,该算例计算结果表明PVJ 计算的位移响应稳定收敛,可有效解决复阻尼模型不能计算结构自由振动响应的问题.

图2 结构的自由振动响应时程Fig.2 Time-history curve of structural free vibration displacements
体系初始时刻处于静止状态,分别采用PVJ 和复阻尼模型时域计算方法(FZ)计算在迁安波地震作用下的位移响应时程,并与复阻尼模型的频域计算方法(FFZ)的计算结果进行对比(如图3 所示),其中FFZ 的计算结果可视为精确解[8].当地震作用持续时间大于15 s 时,FZ 计算的位移响应开始明显发散,因此基于复阻尼模型的时域计算方法仅能适用于地震作用持续时间较小的情况.当地震作用持续时间小于12 s 时,PVJ、FZ 和FFZ 计算的位移响应近似相等.整个时程过程中,PVJ 计算的位移响应不受地震持时的限制,位移响应一直稳定收敛.PVJ 的位移在8.15 s 处达到最大值,FFZ 的位移在8.18 s 处达到最大值,且相对误差为6.25%(见表1).因此,PVJ 与FFZ 的计算结果近似相等,证明了PVJ 的正确性.

图3 不同阻尼模型下结构的位移响应时程Fig.3 Time-history curves of structural displacements with different damping models

表1 迁安波作用下峰值结构位移响应对比Tab.1 The comparison of peak structural displacements under Qian-an wave
FFZ 为频域计算方法,仅能计算初始时刻为静止状态的结构动力响应.相比FFZ,PVJ 为时域计算方法,可计算结构自由振动响应和地震作用下非静止初始状态的结构动力响应,克服了FFZ 的缺陷.
3.2 多自由度体系
如图4 所示,以3 层剪切型钢筋混凝土框架结构为例,其损耗因子为0.1.
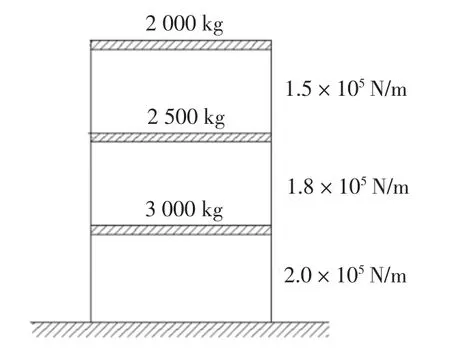
图4 框架结构的质量和刚度分布Fig.4 The mass and stiffness distribution of frame structure
质量矩阵为

刚度矩阵为
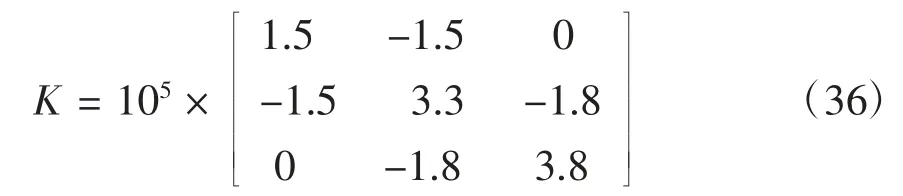
框架结构的初始处于静止状态,分别采用PVJ、FZ 和FFZ 计算结构在El Centro 波和天津波作用下的地震反应,所得位移时程如图5 所示.在图5(a)、图5(b)中,当地震作用持续时间分别小于12 s、15 s时,PVJ 的计算结果与FZ 的计算结果一致.但是,随着地震作用持时增加,FZ 的数值计算结果出现发散现象,这是复阻尼模型自由振动方程通解中包含发散解所引起的.相比之下,PVJ 一直具有稳定收敛的优点.El Centro 波作用下,PVJ 和FFZ 的位移均在4.2 s 处达到最大值,且相对误差为6.60%;PVJ 的位移在8.77 s 处达到最大值,FFZ 的位移在8.79 s 处达到最大值,且相对误差为5.20%(见表2).PVJ 与FFZ 的计算结果近似相等,进一步证明了本文提出的改进频率相关黏性阻尼时程计算方法的正确性.
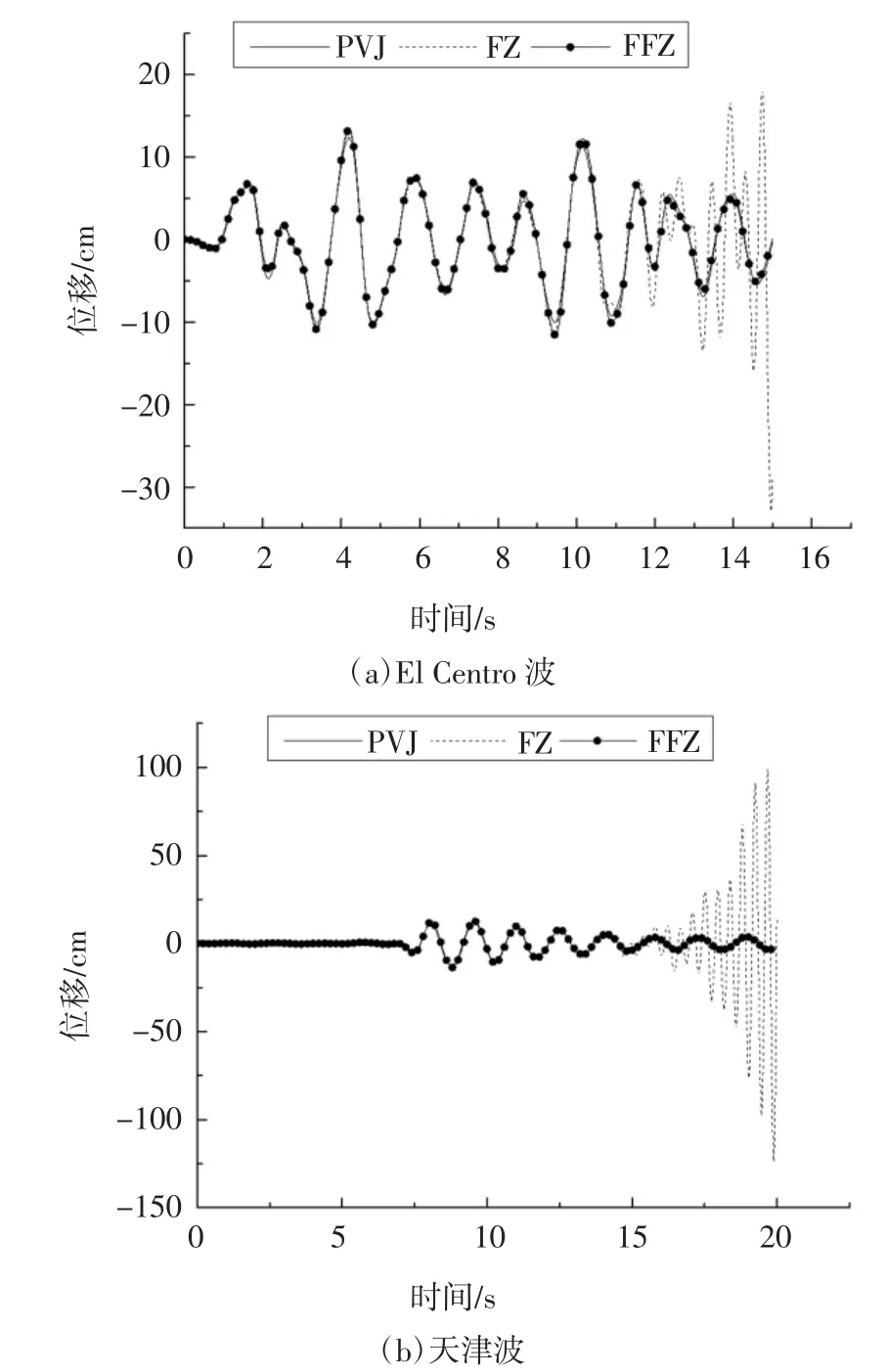
图5 不同阻尼模型下结构顶层的位移响应时程Fig.5 Time-history curves of structural top displacements with different damping models

表2 结构顶层峰值位移响应对比Tab.2 The comparison of peak displacements of top floor
4 结论
经理论推导和算例分析,得到以下结论:
1)引入加速度与位移关系假定,提出了基于复阻尼模型的改进频率相关黏性阻尼模型,可有效克服黏性阻尼模型中耗散能量与外激励频率相关的缺陷.
2)与迟滞阻尼模型相比,基于加速度和位移关系的改进频率相关黏性阻尼模型克服了迟滞阻尼模型中能量耗散与实际不符的缺陷,还保证了单一振动频率下单自由度结构的线性特征.
3)结合常平均加速度法和模态叠加法,推导了改进频率相关黏性阻尼运动方程时程计算的相关公式,算例分析表明,改进频率相关黏性阻尼模型可克服复阻尼模型频域法的缺陷,同时有效避免复阻尼模型时域法计算结果的发散现象.
