考虑桥面不平顺随机激励的车桥耦合方程精细积分解法

2020-10-11陈水生夏钰桓

北京交通大学学报 2020年4期

赵辉，陈水生，夏钰桓

(1.华东交通大学土木建筑学院，南昌 330013; 2.湖北恒大建设工程有限公司武穴分公司，湖北武穴 435400)

结构在移动荷载作用下的振动响应求解是非常经典的力学问题，特别是针对梁结构的研究成果也较多，但是大多研究是把移动荷载简化为移动集中力或移动弹簧质量系统，对结构动力学方程的求解多数采用常规的中心差分法﹑Wilson-θ法﹑Newmark-β法等.

文献[1-9]采用Newmark-β法求解车桥耦合动力方程，在每一个时间步内，移动车辆的位置和车桥相互作用力的大小都是固定不变的，下一个时间步的车桥耦合力是突然施加到桥梁单元节点上,且力的大小也是突然改变的．实际上，车桥耦合力在时间和空间内是连续变化的，并非在一个时间步内固定不变，如果时间步长较大，会造成较大的计算误差，特别是桥面不平顺中的高频成分，很难保证计算的精确，要想获得高精度的计算结果，就必须减小时间步长．文献[10]提出了求解结构动力方程的精细积分方法(Precise Integration Method，PIM)，尽管使用较大的时间步长，依然可以得到动力方程的高精度解.文献[11]采用精细积分法求解简支梁的强迫振动响应.文献[12]提出一种将精确时间积分法与模态分解法相结合的方法来计算粘弹性地基梁结构的响应；文献[13]采用精细积分法求解了简支梁在空间域连续移动简谐荷载作用下的振动响应，研究表明较粗的结构单元和较大的时间步长也能获得很高的计算精度；文献[14]首次将虚拟激励法和精细积分法相结合求解简支梁在移动简谐荷载作用下的振动响应；文献[15]采用虚拟激励法将随机移动荷载转化为确定性荷载，然后精细积分法求解斜拉桥主梁的振动响应；文献[16]以简支梁在匀速移动质量激励下的振动响应为例,分析了时间步长对精细积分法求解精度的影响；文献[17]研究表明采用科茨积分可以提高精细积分法中Duhamel非齐次项的求解精度；文献[18]给出了精细积分法求解简支梁与匀速移动弹簧质量单自由度车辆模型的耦合振动方程；文献[19]将车辆简化为多刚体模型，轨道简化为三层梁模型，采用精细积分法计算了大型车辆-轨道耦合模型的响应.

但是，上述文献都是把桥梁结构简化为欧拉伯努利简支梁模型，车辆荷载简化为移动集中力、单自由度弹簧质量或两自由度弹簧质量模型，忽略了桥面不平顺随机性对桥梁振动响应的影响．实际的桥梁和车辆都是空间三维结构，桥面不平顺也存在很大的随机性，并且车辆的6个车轮在桥上连续移动，与车轮直接接触的桥面单元的每一个节点在每一时间步都要进行动态分解．

因此，本文作者借助有限元方法建立桥梁的空间三维模型，采用广义坐标离散的方法将桥梁结构进行单元离散，并将一辆三轴重载汽车简化为三维9自由度空间模型，求解桥梁在桥面不平顺随机激励下的振动响应.根据壳单元的插值函数，推导车辆各轮在所接触壳单元4个节点进行等效节点力分解的计算公式；基于虚拟激励法(Pseudo Excitation Method，PEM)将复杂的随机桥面不平顺转化为一系列虚拟的确定性激励，充分利用结构动力方程精细积分求解方法的优点，在频域内分析桥梁的振动响应.与传统时域方法求解桥梁振动响应相比，本文求解三维车桥耦合振动方程的的精细积分方法不仅计算速度快，而且求解结果精度高.

1 车桥耦合方程的建立

1.1 车辆振动方程

以一辆三轴重载自卸汽车为研究对象，采用传统的弹簧质量阻尼振动体系，将车辆简化为三轴9自由度空间模型，考虑车体竖向振动、纵向点头、侧翻以及车轮振动，车辆前轴重64.7 kN，中后轴重258.8 kN，车辆模型如图1所示.

图1中：ks1、ks2、…、ks6分别为各轴悬架弹簧刚度；kt1、kt2、…、kt6分别为各车轮刚度；cs1、cs2、…、cs6分别为各轴悬架阻尼系数；ct1、ct2、…、ct6分别为各车轮阻尼系数；m1、m2、…、m6分别为各悬架系统质量；mhb、Ihb、Ir分别为车体质量、车体俯仰转动惯量和车体侧倾转动惯量；θb、φ、zb分别为俯仰角、侧倾角和车体竖向位移；z1、z2、…、z6分别为各轴悬架位移坐标；车辆参数参考文献[20]．

依据振动原理，建立9自由度车辆振动方程如下

(1)

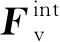
1.2 桥梁振动方程

为减少车桥耦合计算矩阵维数和计算工作量，采用模态综合叠加技术建立桥梁的振动方程

(2)

式中：Fg为车辆自重引起的各车轮作用点处的荷载向量；ξm为桥梁第m阶阻尼比；ωm为桥梁第m阶自振频率；Φ为桥梁m阶振型向量矩阵；q为桥梁广义坐标列向量．其中，

1.3 车桥耦合方程

通过车轮与桥面接触处的位移协调条件和相互作用力平衡条件，建立车桥耦合振动方程．考虑桥面不平顺随机激励的影响，第i个车轮作用在桥梁上的荷载可以写成

(3)

式中：N为桥面壳单元的插值函数；Φ为桥梁m阶振型向量矩阵；ri为第i车轮的桥面不平度值；v为车辆行驶速度；Fgi为第i车轮的车辆自重.

联立式(1)～式(3)，可得车桥耦合振动方程

(4)

(5)

(6)

2 桥面不平顺的虚拟激励构造

针对桥面不平顺的激励，通常是采用一条不平顺记录或由不平顺功率谱随机生成一条时间历程样本作为系统激励输入，通过逐步积分求解系统响应，这其实只是桥面不平顺激励的一次实现，虽然可以采用蒙特卡罗法对多条桥面不平顺样本进行分析和统计处理，但必须取足够的样本才能确保统计的准确性，且耗费大量的计算时间.为了克服这一不足，采用虚拟激励法，将复杂的随机桥面不平顺转化为一系列虚拟的确定性激励，计算方便且精度较高.

随机道路不平顺是一随机过程，具有各态历经性，其不平顺高程的描述国际上通常采用频域方法，用功率谱密度来进行标定，其表达式为

Gq(n)=Gq(n0)(n0/n)2

(7)

式中：n0为空间参考频率,n0=0.1,1/m；n为空间频率；Gq(n0)为路面不平度系数，与路面等级有关.

考虑车辆左右轮的相干关系和前后轮的时间滞后，利用车辆各轮间的频响函数关系，可以推得六轮车辆路面激励功率谱密度矩阵为

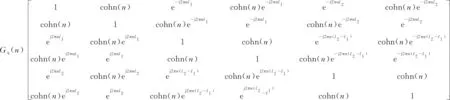
(8)

式中：cohn(n)为左右轮迹的相干函数，其随空间频率n的取值不同而在0～1内变化.

可进一步将六轮车辆桥面激励功率谱密度矩阵写成如下形式

Gqq(ω)=V*SρSV

(9)

(10)

(11)

(12)

式中：ρ为车辆各轮间的相干函数矩阵，是实对称正定矩阵.V*为各车轮时间效应函数矩阵V的共轭矩阵.

如果只考虑桥面不平顺随机激励荷载Fw作用，车桥耦合振动方程式(4)可写成

(13)

由 (6)式可知，桥面不平顺激励荷载Fw有两部分组成：桥面不平顺竖向位移及其一阶导数的速度项，在此将Fw分成位移引起的荷载项Fw1和速度引起的荷载项Fw2，计算式为

Fw=Fw1+Fw2=

(14)

式中：

则可以构造如下虚拟激励荷载

(15)

ρ=QQT

(16)

式中：Ie为单位列向量；V为各车轮时间效应函数矩阵；Q是实对称正定矩阵ρ的分解项．

将式(15)的虚拟激励荷载代入式(13)，得到虚拟振动响应的方程式

(17)

3 车桥相互作用力的节点等效分解

精细积分法求解桥梁在移动荷载作用下的振动响应，已有研究都是将桥梁简化为梁单元，移动荷载简化为集中力或平面车辆模型，根据梁单元的插值函数将移动荷载等效分解到梁单元的2个节点上[11-20]；而实际的车辆和桥梁都是空间体系，车桥耦合作用复杂，三维车辆的各个车轮荷载同时作用在桥面板上，车桥耦合系统并非简单的平面体系.因此,有别于已有研究，本文考虑三维车辆各车轮的空间和时间关系，将车辆各轮的作用力按照壳单元的插值函数等效分解到各车轮直接作用的桥面壳单元4个节点上，用精细积分法求解桥梁在多轴车辆作用下的振动响应，见图2.

桥面第n个壳单元沿整体坐标x方向的长度为2a，沿y方向的长度为2b，第i个车轮自壳单元的一端沿整体坐标x方向向另一端以速度v匀速行驶．在数值计算的某一积分步长Δt内，第i个车轮由A点移动到B点，这时A、B两点均在第n个壳单元内，tk时刻车轮作用于A点，而xk+1时刻车轮移动到B点，A点距离所在壳单元起始端为x1，B点距离所在壳单元起始端为x2．假设任意k时刻，第i个车轮所在的壳单元起始端距桥梁起点的距离为xk，则第i个车轮在第n个壳单元内到壳单元起始端的距离x和局部坐标ζ为

x=vtk-xk,ζ=β1t-β2

(18)

式中：β1=v/a；β2=xk/a.

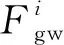
(19)

式中：Nj(ζj,ηj)，j=1～4是壳单元的插值函数

Nj(ζj,ηj)=

(20)

将式(18)代入式(20)，可得

(21)

利用荷载的节点等效，桥面板上的外荷载向量可以表示成

F(t)=

(22)

将式(19)和(21)代入式(22)，可得

(23)

式中：ri是常系数向量.

ri可以表示为

(24)

式中：

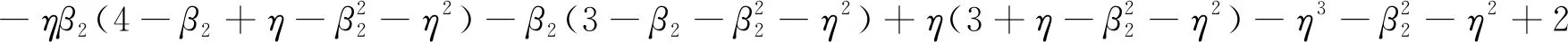
b12=ηβ1β2(3β2+2)-ηβ1(4-η2+η)+β1β2(2+3β2)-β1β2(2η+2)-β1(3-η2)

b13=ηβ1(β1+3β1β2)+β1(β1+3β1β2)-

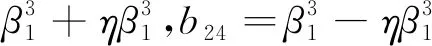
式中，C0(mg·L-1)和Ce(mg·L-1)分别为亚甲基蓝溶液的初始浓度和平衡浓度；m(mg)为吸附剂投加量；Qe(mg·g-1)为平衡吸附容量。

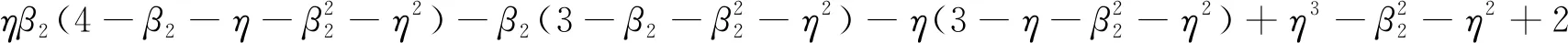
b22=ηβ1β2(-3β2-2)+ηβ1(4-η2-η)+β1β2(2+3β2)-β1β2(-2η+2)+β1(-3+η2)

b23=ηβ1(-β1-3β1β2)+β1(β1+3β1β2)+

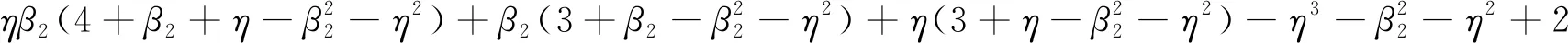
b32=ηβ1β2(-3β2+2)+ηβ1(4-η2+η)+β1β2(2-3β2)-β1β2(2η+2)+β1(3-η2)

b33=ηβ1(β1-3β1β2)+β1(β1-3β1β2)-

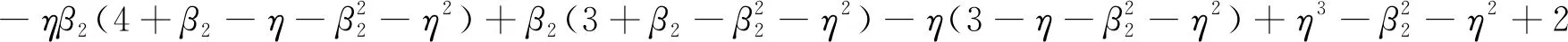
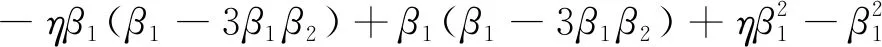
4 车桥耦合方程的精细积分求解

将虚拟激励荷载引起的确定性运动方程式(17)转化成状态方程

(25)

式中：

方程(25)的通解为齐次解vh(t)与特解vp(t)之和，即

v(t)=vh(t)+vp(t)

(26)

假设tk时刻，状态量为v(tk)，则在tk+1=tk+Δt时刻，桥梁的状态向量v(tk+1)为

v(tk+1)=T(Δt)[v(tk)-vp(tk)]+vp(tk+1)

(27)

式中：T(Δt)为指数矩阵；vp(tk)为特解向量.

在某一积分步t∈(tk,tk+1)中，齐次解为

vh(t)=T(τ)c

(28)

式中：T=exp(H(τ)),利用指数函数的加法定理，可以对其进行精细计算[10-13];τ=t-tk；c为由初始状态t=tk所决定的积分常量.

方程(25)的解可以写成

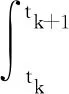
(29)

对式(29)进行离散，可得

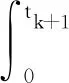
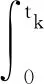
(30)

式(30)的第二项为杜哈梅尔项，可以采用科茨积分计算

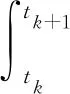
(31)

从上述推导过程可以看出，车桥耦合方程式(13)的精细积分法解法，只用于定常系统[21]，即车桥相互作用模型的Mbv、Cbv、Kbv为常数矩阵．但精细积分法与常规动力方程求解方法Newmark-β法相比，前者不受时间步长的限制，桥面不平顺中的高频成份不会丢失，取较大的时间步长也能够得到动力方程的精确解[18]．

5 算例分析

以江西奉铜高速公路上的某预应力混凝土简支T梁桥为研究对象，桥梁上部结构6片T梁组成，T梁高2 m，单片梁宽2.1 m．桥面横向布置形式为0.5 m(防撞栏)+11.65 m(行车道)+0.5 m(防撞栏)．桥面铺装层采用4 cm厚改性沥青混凝土抗滑表层+6 cm厚中粒式改性沥青混凝土+三层FYT-1改性防水层+10 cm厚C50混凝土桥面铺装层.采用ANSYS建立桥梁三维有限元模型，主梁、桥面现浇层和横隔板材料主要由C50混凝土组成，材料弹性模量为34.5 GPa，密度为2 600 kg/m3，泊松比0.167；两侧护栏C30混凝土弹性模量为30 GPa，密度为2 400 kg/m3，泊松比0.167；面层沥青混凝土材料弹性模量为1.2 GPa，密度为2 360 kg/m3，泊松比0.2；主梁、桥面现浇层和护栏采用实体单元建立，横隔板和面层沥青混凝土用壳单元建立，桥梁有限元模型见图3，前10阶基频及振型特征见表1．

为研究方便，在此只考虑一种荷载布置方式，车辆按正常行车道位置行驶，荷载作用在②梁上，距离防撞栏1.475 m，桥梁每片T梁分别编号，荷载布置见图4．桥面不平顺随机激励考虑车辆前后轮的时间滞后和左右轮的相干性，采用文献[22]的相干函数模型，模型表达式为

cohn=e-2πnB=e-ωB/v

(32)

式中：B为车辆左右轮间距；v为车辆行驶速度.

5.1 虚拟激励法+精细积分法的验证

为进行对比验证，首先将三角级数叠加法生成的多个桥面不平顺随机激励样本代入车桥耦合方程式(4)计算桥梁振动响应，然后采用传统蒙特卡罗法(Monte Carlo Method，MCM)分别对200、2 000、5 000个桥梁振动响应样本进行统计分析，并与虚拟激励法+精细积分法(Pseudo Excitation Method+Precise Integration Method，PEM+PIM)对比.当车辆以72 km/h的速度行驶在B级桥面上时,桥梁边梁跨中竖向位移和车体竖向位移的标准差曲线见图5。从图5可以看出，蒙特卡罗法5 000个样本计算出的标准差曲线远远好于200个样本；蒙特卡罗法200个样本的边梁跨中竖向位移标准差与PEM+PIM计算结果的最大偏差为11.8%， 2 000个样本的最大偏差为4.68%，5 000个样本的最大偏差为2.13%，随着蒙特卡罗法样本数的增加，其计算结果越来越接近PEM+PIM的计算结果；PEM+PIM的计算时间为24.5 s，而蒙特卡罗法200个样本的计算时间为40.13 s，2 000个样本的计算时间为396.98 s，5 000个样本的计算时间为998.34 s，耗费的计算时间随样本数量的增加而增加，可见PEM+PIM不受样本数量的限制，计算速度和精度明显提高．

针对车桥耦合方程的求解，也可以在虚拟激励法的基础上，采用Newmark-β法求解车桥耦合系统的振动响应，但Newmark-β法采用1 739积分步、耗时400.61 s，才获得与精细积分法采用174积分步、耗时24.5 s基本相同的计算结果.求解的桥梁边梁跨中竖向位移和车体竖向位移标准差曲线如图6所示，在计算结果基本相同的情况下，精细积分法的计算效率明显高于常规Newmark-β法.

5.2 精细积分法求解桥梁的振动响应

5.2.1 桥梁振动响应的均值

当车辆以不同的速度在B级桥面行驶时，精细积分法求解的桥梁边梁跨中竖向位移响应均值见图7.从图7可以看出，在桥面路况相同的情况下，不同车辆行驶速度对桥梁跨中竖向位移响应的均值影响不大；当车辆以相同的车速60 km/h行驶在不同路况等级的桥面上时，桥面路况对边梁跨中竖向位移响应均值的影响见图8.由图8可知，同一行车速度，桥梁振动响应的均值随着桥面路况的恶化而变化较小；由此可见，桥梁振动响应的均值主要还是由车辆重力这一确定性荷载引起．

5.2.2 桥梁振动响应的标准差

研究车桥耦合振动,考虑桥面不平顺激励的多点输入更符合真实的车桥实际关系状态，车辆六轮的多点时间相关激励和双轮辙多点空间相关激励使得桥面随机激励输入模型更加精细，并且桥面的不平顺状况具有很大的随机性.因此，本文基于虚拟激励法考虑车辆六轮的相干关系和时间滞后关系，采用精细积分法求解桥梁的振动响应．当车辆在B级桥面行驶时，桥梁每片T梁跨中竖向位移和加速度响应标准差最大值与车辆行驶速度的变化关系见图9.由图9可知，虽然桥梁振动响应的标准差受行车速度的影响较大，但振动响应的最大值与车辆行驶速度并非成线性比例关系，并且加速度响应对车辆速度的变化更为敏感；当车速小于90 km/h时，同一片梁振动响应标准差最大值随着行车速度的提高而有不同程度的增大，振动响应的离散程度加大；不同片梁的振动响应标准差最大值随车速的变化而趋势一致，距离荷载作用位置较近的梁振动响应大于远处梁的振动响应；在车速为90 km/h时，桥梁振动响应出现一个峰值，即产生了车桥耦合共振现象；当车速大于100 km/h时，桥梁振动响应标准差最大值随车速的变化又出现了缓慢上升的趋势.

当车辆以80 km/h的速度在不同路况等级的桥面上行驶时，边梁跨中竖向位移和加速度响应的标准差时程曲线见图10，由图10可知，桥梁振动响应的标准差对桥面不平顺等级的变化非常敏感，随着桥面路况的恶化，桥梁振动响应的标准差成倍增加，可见控制桥面不平顺是减小桥梁振动的一个有效措施．

5.2.3 桥梁振动响应的最值估计

桥面不平顺常看作是平稳的、服从高斯分布的随机过程，根据随机振动理论，线性系统下的桥梁振动响应也应该满足平稳高斯分布．求出桥梁在桥面不平顺随机激励下的振动响应均值μ和标准差σ，由概率统计理论可知，桥梁的振动响应落在(μ-3σ,μ+3σ)之外的概率通常小于3‰，根据小概率事件的实际不可能原理，区间(μ-3σ,μ+3σ)常看做随机变量的实际可能的取值区间，这一原理称为三倍标准差原理．因此，采用三倍标准差原理，就可以估算桥梁振动响应的取值范围，得到振动响应的最大值和最小值．考虑车辆六轮桥面随机激励的相关性，当车辆以60 km/h速度行驶在B级桥面时，边梁跨中竖向位移和加速度的最值时程曲线及三条样本曲线如图11所示，从图11可知，虽然桥梁的振动响应随机性很强，但超过最大值和最小值所组成带状区域的概率只有3‰，任意一个样本都满足三倍标准差原理，三条样本曲线都围绕着均值上下波动且在最大值与最小值之间；桥梁边梁跨中竖向位移响应的最大值和最小值曲线靠得较远，而竖向加速度响应的最大值和最小值曲线基本呈对称分布，可见桥面不平顺对桥梁振动加速度的影响大于对桥梁振动位移的影响；结合图8和图10还可以看出，桥面路况越差，最值所组成的带状区域宽度就会越大，因为路况差，导致桥梁振动响应的离散程度加大，标准差增大，而响应的均值对桥面不平顺等级和行车速度不敏感．

根据三倍标准差原理，车辆在B级桥面上行驶时，边梁和次边梁的跨中位移和加速度响应极大值随速度的变化关系见图12.

结合图9可以看出：标准差小，响应的极大值就小，标准差大，响应极大值就大；桥梁振动响应的极大值与响应的标准差密切相关，即与桥面不平顺的随机性有很大关系，其取决于振动响应的离散程度．

5.2.4 桥梁振动响应的功率谱分析

采用虚拟激励+精细积分法计算桥梁①梁和②梁跨中截面竖向振动加速度的功率谱，如图13所示，从图13可知，①梁和②梁跨中竖向加速度的功率谱密度在多个频率处出现峰值，振动频率主要集中在4.12、13.13～15.2、18.13、25.92 Hz，分别与桥梁的1、3、5、8阶基频接近，可见桥梁的竖向振动响应主要受前几阶竖向弯曲振型控制.