基于虚拟闭合法采用梁单元计算裂尖节点力的方法

贾昕昱，黎国清，刘秀波

(1.中国铁道科学研究院，北京 100081；2.中国铁道科学研究院集团有限公司 基础设施检测研究所，北京 100081)

断裂力学是一门起源于生产实践的新兴学科，主要研究材料及结构的破坏问题.由于这些问题往往与结构的安全运行以及服役寿命有关，因此这门学科在短时间内就有了迅速的发展.Griffith[1]研究了玻璃内部细小裂纹引起的应力集中，建立了脆性材料裂纹尺寸与断裂强度之间的关系.Irwin[2]在Griffith的基础上提出了能量释放率的概念.Rice[3]研究了非线性材料的能量释放率，指出非线性材料的能量释放率可由线性积分表示，并将这一方法命名为J积分.这些初始的理论解将人们带入到断裂力学的领域中，并对促进断裂力学发展起着巨大作用.然而，由于现实问题中裂纹形态的多样性以及作用载荷的复杂性，这些理论解并不能解决实际中所遇到的各类复杂问题.随着计算机技术的发展，人们越来越多地将目光放到了采用数值方法计算断裂问题的层面，比如有限差分法[4]、边界元法[5]及无网格法[6].但是，由于这些方法与商业计算软件结合度不高，而且应用这些方法的门槛也较高，因此这些方法并没有得到较好的普及.

在计算裂纹尖端的能量释放率时，虚拟裂纹闭合法(Virtual Crack Clastre Meched,VCCT)是一种非常可靠、高效的方法.该方法由Rybicki等[7]提出，可通过裂纹尖端的节点力以及裂纹后端节点的相对位移计算出能量释放率.该方法中的节点力及节点位移都是有限元软件中的基本量，可以方便的获取，并且该方法对裂纹附近网格尺寸的要求不高，也不需要使用奇异单元.Shivakumar等[8]将VCCT从二维问题扩展到三维问题，并且证明了在计算表面裂纹时VCCT的正确性.刘明尧等[9]分析了采用1/4节点位移法、位移外推法、VCCT计算裂纹尖端应力强度因子的异同，得出这三种方法的结果基本一致，都可以很好地描述出裂纹尖端的受力状态.

在铁路领域，滚动接触疲劳裂纹是钢轨上非常常见的一种伤损形式，在车轮的反复滚动作用下，钢轨接触区附近的浅表层会产生疲劳裂纹，这些裂纹如果不及时处理，就会进一步的发展，导致钢轨轨距角处发生剥离掉块，严重的甚至会发生断轨，危及行车安全.因此，裂纹的扩展分析就变得非常重要.赵小罡等[10]采用VCCT计算了在轮轨接触区钢轨直裂纹的扩展影响因素.VCCT也被应用于多种裂纹计算领域中.Xie等[11-12]采用VCCT分析了任意裂纹形状在受到作用力时的扩展路径，并与其他方法所得结果进行对比，具有较好的一致性.姚安林等[13]分析了管道中多条平行裂纹之间的干涉效应.

VCCT虽然被应用于多种裂纹计算领域，但是较少有文章对于该方法与有限元软件之间的有机联系进行优化.本文作者将基于离散梁单元对裂纹尖端的节点力进行计算，并考虑不同因素对计算结果的影响，同时对钢轨存在斜裂纹时的扩展状态进行分析，验证模型的正确性.

1 理论基础

在诸多计算裂纹问题的方法中，虚拟闭合法是一种非常有效的数值处理方法.该方法的原理是，裂纹在扩展一个Δa的距离时，势能的改变与闭合该增量所需的功等效.图1为裂纹尖端有限元网格示意图，其中，(1)、(2)、(3)、(4)为单元号，1、2、3、5为节点号.计算能量释放率的公式为

GⅠ=(Fy1Δv2,3)/(2BΔa)

(1)

GⅡ=(Fx1Δu2,3/2BΔa)

(2)

式中：GⅠ、GⅡ分别为Ⅰ型及Ⅱ型裂纹的能量释放率；Fx1、Fy1分别为节点1在x、y方向的节点力；Δu2,3、Δv2,3分别为2、3点在x、y方向的相对位移；B为板的厚度；Δa为单元宽度.

在计算能量释放率的公式中，节点2、3的相对位移可由结果中的节点坐标直接得出，而节点1的节点力无法从结果文件中直接得出，需要进行相应的计算.由于公式中的节点力为内力，因此 (1)、(2)、(3)、(4)号单元都对节点1的节点力有一定的贡献.如果裂纹面上没有受到外力的作用，如图2所示，则节点力在x、y方向上的合力均为零，即

(3)

(4)

式中上标为单元编号.节点1处裂纹面一侧的总节点力，可以通过单元(1)、(2)求得，也可以通过单元(3)、(4)求得

(5)

(6)

在计算裂纹面一侧总节点力时，需要先找到裂纹面一侧的单元，通过单元的正应力、剪应力及单元中各节点的坐标推导得出单元在相应节点处的节点力，再将这些单元在此节点处的节点力相加，才能得到所需的节点力.这样会带来大量复杂的后处理计算，提高了虚拟闭合法的使用门槛，削弱了虚拟闭合法与有限元计算的联系.为了解决这一问题，这里将应用梁单元来计算裂纹尖端的节点力.

LS-DYNA是一款非常先进的通用非线性有限元程序，在动力学分析领域具有很强的实力.离散梁单元是基于梁单元的一种单元形式，如图3所示.图中r、s、t代表梁单元中的局部坐标系，节点I、J定义为梁单元的两个端点，节点K定义为截面初始方向.在离散梁单元中，可以定义沿着r、s、t方向的刚度.离散梁单元可以是有一定长度的，也可以是0长度的.当单元为0长度时，离散梁的方向由r、s、t决定.通过定义r、s、t的方向就可得出离散梁单元的方向，并且单元的内力可以在r、s、t的方向上进行输出.一个离散梁单元有6个自由度，而弹簧单元只有1个自由度，因此该单元可以更好地模拟复杂情况下裂纹的受力状态.

基于以上背景，采用在裂纹尖端施加离散梁单元来计算节点力的方法，如图4所示.该方法为，在图1的裂纹尖端节点1处，将两个连接单元(2)、(3)分离，然后将分离后出现的节点1及节点4采用离散梁单元进行连接.由于离散梁单元可以定义3个方向的刚度，因此可以通过节点的相对位移得出节点在3个方向的力，如图5所示.

图5中，U、F分别表示离散梁单元两端节点的位移及力，节点力和节点位移之间的关系为

F1=Kx(U1-U4)

(7)

F2=Ky(U2-U5)

(8)

F3=Kz(U3-U6)

(9)

F4=Kx(U4-U1)

(10)

F5=Ky(U5-U2)

(11)

F6=Kz(U6-U3)

(12)

式中：Kx、Ky、Kz为沿x、y、z方向的刚度.表示为

(13)

即F=KU，K为刚度矩阵.

2 有限元模型验证

2.1 不同方向应力强度因子验证

通过有限元模型与理论结果进行对比，验证该方法的正确性.首先，分析了含有穿透型斜裂纹的薄板受到均布拉力作用时，裂纹尖端的受力状态，如图6所示.图6(a)为薄板及裂纹尺寸示意图，图6(b)为有限元示意图.薄板的宽度W=5 m，长度H=10 m，裂纹长度a=2 m，裂纹角度θ=45°，板厚t=0.1 m，密度为7 800 kg/m3，拉应力σ=10 kPa，梁刚度为1×1011N/m，薄板的泊松比υ=0.3，弹性模量E=200 GPa.

由于此例中的裂纹为斜裂纹，需要将全局坐标系下的力及位移转换到局部坐标系下，如图7所示.裂纹角度为θ，节点1和节点5的距离为

(14)

全局坐标系下和局部坐标系下节点力及节点相对位移的关系为

(15)

(16)

(17)

应变能释放率为

(18)

应力场强度因子为

(19)

式中：E*为材料的弹性模量，在平面应力情况下，E*=E；在平面应变情况下，E*=E/(1-υ2).

所得结果如表1所示.

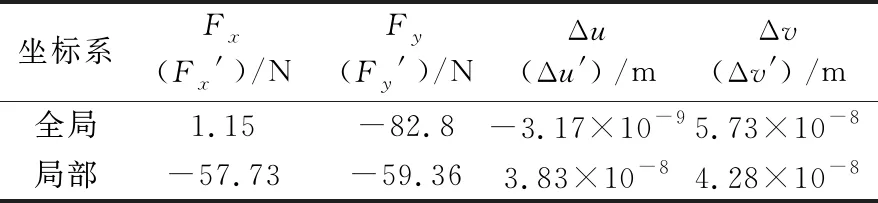
表1 有限元计算结果

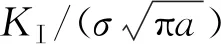
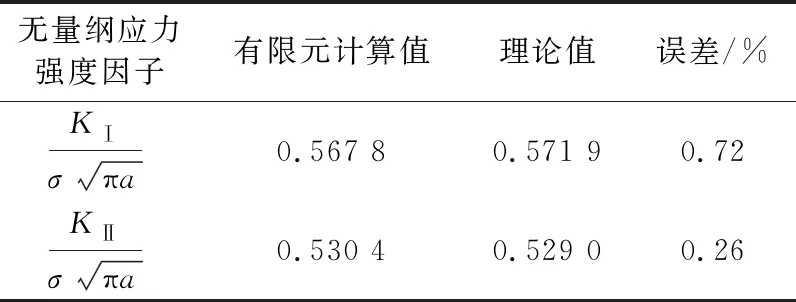
表2 有限元结果与理论值对比

2.2 网格尺寸的影响分析

为了分析该方法是否能应用于不同的裂纹形态，随后计算了一种半圆柱体内嵌半圆形裂纹的情况，如图8所示.图8(a)为半圆柱体的示意图，图8(b)为裂纹面网格截面图.半圆柱体的半径R=0.6 m，高H=1.2 m，裂纹的半径r=3 mm，拉应力σ=1 kPa，梁刚度为1×1011N/m，半圆柱体的密度为7 800 kg/m3，泊松比υ=0.3，弹性模量E=200 GPa.内嵌半圆的应力强度因子理论值[15]为

(20)

λs=1.04[1+0.1(1-sinθ)2]

(21)

随后，分析了裂纹尖端不同网格尺寸对计算结果的影响.由于裂纹面的半径为3 mm,因此选取了3种网格尺寸，分别为0.15、0.28、0.5 mm.有限元计算值与理论值结果如图9所示，x轴的θ为裂纹尖端的角度，y轴的K1为Ⅰ型应力强度因子，图中的数据曲线分别表示理论计算值以及不同网格尺寸的有限元模拟值.从图9中可以看出，当裂纹尖端有限元网格尺寸为0.5 mm时，计算值与理论值偏差较大，最大误差发生在θ=20°及θ=160°，为14.2%；当网格尺寸为0.28 mm时，最大误差发生在θ=0°及θ=180°，为2.6%；当网格尺寸为0.15 mm时，最大误差发生在θ=6°及θ=174°，为4.1%.导致计算值与理论值之间产生误差的原因主要有以下几个方面：①理论值中的半圆柱体是无限大体，但是在有限元计算中受到边界条件的影响会对计算结果产生一定的干扰.②在采用有限元划分网格时，裂纹的前缘被离散化，由多条直线段组成，而不是理论公式中的完全光滑的半圆，因此也会带来一定的误差.可以得出，当网格尺寸在0.28及0.15 mm时已经可以满足精度的要求，而采用0.28 mm网格又可以减少单元数量，提高计算效率，因此随后的计算中将选择采用0.28 mm的网格.

2.3 梁刚度的影响分析

由于在采用离散梁单元时需要设置梁单元在局部坐标系r、s、t三个方向上的刚度，本文将分析不同刚度对计算结果的影响.梁的刚度需要设置为一个相对较大的值，以此来保证裂纹尖端的节点处于闭合状态.选取2.2节中的模型进行分析，在r、s、t三个方向上取相同的刚度值，分别对1×108、1×109、1×1010、1×1011、1×1012、1×1013六种情况进行计算，结果如图10所示.刚度为1×108时，与理论值的偏差较大，最大误差为6.5%.当刚度为1×109～1×1013这五种情况时，各计算值基本相同，最大误差分别为3.5%、3.2%、3.1%、3.1%、3.1%.从计算结果可以得出，离散梁的刚度值在一个非常大的范围内都可以满足计算精度的要求.

2.4 结构刚度影响分析

由于采用梁单元计算裂尖节点力的方法改变了裂纹尖端的位置，因此随后验证该方法是否会改变结构的刚度.采用上述半圆柱体内嵌半圆裂纹模型，分析在相同受力状态下施加梁单元及不施加梁单元时对裂纹面上节点的相对位移的影响，如图11所示.图11中红色线为裂纹尖端的位置，绿色线为所求的裂后节点.在板的两端施加均布载荷，分别计算两种情况下节点的位移，如图12所示.从图12中可以看出，有无梁单元时，裂纹尖端后部节点变形量的差距不大，最大误差为0.043%，可以认为梁单元的加入对结构的刚度影响可以忽略.

3 钢轨斜裂纹扩展分析

在重载铁路中，钢轨斜裂纹是一种非常普遍的现象，如图13所示，图中斜裂纹分布于钢轨轨距角处，与行车方向呈60°夹角，并且呈平行分布.采用梁单元计算裂尖节点力的方法，对重载铁路斜裂纹的扩展做一个初步的探讨.

根据重载铁路中实际的轨道参数及车辆参数，建立了轮轨滚动接触有限元模型，如图14所示.图14(a)为轮轨有限元模型，钢轨为75 kg/m轨，轨底坡为1∶40，没有设置超高.车轮踏面为LM型，车辆轴重为25 t，一系弹簧以上的部分简化为质量点，通过弹簧阻尼单元施加到车轴上.图14(b)为在钢轨上设置了一条位于轨距角处的斜裂纹，斜裂纹位于钢轨表面，长为3.5 mm，深为1.5 mm，与行车方向呈60°夹角.车辆行进的速度为90 km/h.

斜裂纹的有限元模型如图15所示，图中裂纹的角度与图14(b)中所示角度一致.根据文献[16]，斜裂纹可以简化为一个椭圆平面，这里也将裂纹面简化为椭圆面，在裂纹尖端分布有16个节点，分别对各节点计算应力强度因子.

为了使车轮能够滚过裂纹面，将轮对向左轨侧横移4 mm，并且轮对绕着纵向(轮对前进的方向)旋转0.029°.当车轮经过裂纹面附近时，钢轨在车轮的作用下应力分布如图16所示.从图中可以看出轮轨的接触斑不是通常的椭圆形，而是偏向于圆形，位于轨距角处，接触斑与裂纹相接触，并且接触压力最大值发生在裂纹面的左端.

随后对裂纹面上各节点的Ⅰ型、Ⅱ型、Ⅲ型应力强度因子进行计算，计算结果如图17所示.从图中可以看出，裂纹面各节点的Ⅰ型及Ⅱ型应力强度因子相对较小，Ⅲ型应力强度因子为最大，也即两个裂纹面主要沿着横向方向相互滑移，并且1号节点处的Ⅲ型应力强度因子最大，也即裂纹面会有向钢轨内侧扩展的趋势.在实际的钢轨斜裂纹中，裂纹是起源于轨距角处，然后向轨头下部进行扩展，说明本文所得结果与实际情况较为吻合，可以用来对钢轨斜裂纹的扩展进行分析.

4 结论

采用虚拟裂纹闭合法计算裂纹尖端应力强度因子时，提出了一种通过梁单元来计算裂纹尖端节点力的方法.该方法可以减少后处理工作中数据多次运算可能带来的误差，减弱后处理的工作强度，降低虚拟裂纹闭合法的使用门槛，提高计算效率，使虚拟闭合法与有限元软件更好的结合，并且该方法也能保证计算精度的要求.通过对比分析，得出以下结论：

1)在对斜裂纹的分析基础上，对于Ⅰ型及Ⅱ型开裂，采用梁单元的方法与理论值的误差最大为0.72%，有较好的准确度.

2)当裂纹的半径为3 mm时，裂纹尖端网格尺寸选为0.28 mm可以既满足精度要求，又满足计算效率要求.

3)离散梁的刚度值可以取一个非常广的范围，在该范围内均可满足精度要求.

4)对钢轨存在斜裂纹的情况进行了分析，当车轮横移4 mm时，接触斑会压过裂纹面，此时裂纹面上的Ⅲ型应力强度因子为最大，两裂纹面以横向滑移为主，并且裂纹会从轨距角处向钢轨内侧扩展.