长杆弹超高速侵彻半无限混凝土靶实验研究及开坑分析*

王 杰，武海军，周婕群，石啸海，李金柱，皮爱国，黄风雷

（1. 北京理工大学爆炸科学与技术国家重点实验室，北京 100081；2. 中国工程物理研究院化工材料研究所，四川 绵阳 621999；3. 中国工程物理研究院总体工程研究所，四川 绵阳 621999）

近年来，对于动能弹侵彻混凝土等硬材料的研究重点已由中低速侵彻转向高速/超高速侵彻。对中低速侵彻混凝土靶的开坑尺寸规律已有大量研究，而长杆弹超高速侵彻混凝土靶的实验研究较少，对弹体超高速侵彻混凝土靶开坑特性的研究仍处于初步阶段。Forrestal 等[1-2]、Qian 等[3]进行了一系列动能弹中低速侵彻混凝土的实验，基于实验数据给出开了坑深度为4 倍弹体直径的经验公式。吴祥云等[4]进行了弹体以初速300 和400 m/s 分别侵彻C25 和C30 靶体的实验，基于实验结果，拟合得到了弹体侵彻半无限混凝土靶板的漏斗状弹坑深度和直径的经验公式。温志鹏等[5]利用吴祥云等[4]的实验数据进行参数拟合，得到了弹坑深度的经验公式。刘海鹏等[6-7]进行了一系列的截卵形头部弹体中低速侵彻有限厚混凝土靶的实验，并对实验结果进行量纲分析，得到了弹体侵彻混凝土靶时的靶面无量纲开坑直径和无量纲开坑深度的表达式。刘海鹏等[8]基于实验数据，还从裂纹扩展和靶体破碎角度出发，计算了漏斗形弹坑尺寸。闪雨[9]开展了一系列弹体以初速度1.0～1.3 km/s 侵彻混凝土靶的实验，并结合Wu 等[10]的实验数据，得到了无量纲开坑深度与弹体初速度的线性拟合关系。薛建锋等[11]基于应力波在混凝土靶自由表面斜反射形成层裂的原理，获得了破碎区径向尺寸和开坑深度的计算公式，并开展弹体斜侵彻混凝土实验对相关分析进行了验证。周宁等[12-13]、黄民荣等[14]分别开展了一系列弹体中低速侵彻35 MPa 混凝土和钢筋混凝土的实验，记录了相应的开坑直径和开坑深度的实验数据，并分析了侵彻过程。张爽[15]针对刚性弹体中低速侵彻钢筋混凝土的开坑过程和整个侵彻/贯穿过程，开展了系统的实验和理论研究。

目前，在超高速侵彻开坑的研究领域，研究对象主要为天体物理中的陨石撞击开坑。Melosh[16]总结了1980 年之前陨石撞击开坑实验研究成果，并对开坑过程进行分阶段量纲分析。Holsapple[17]基于陨石撞击开坑的实验数据，拟合得到了开坑直径无量纲数与靶体材料强度无量纲数的关系。Dufresne 等[18]、Poelchau 等[19]总结了MEMIN（multidisciplinary experimental and modeling impact research network）研究中心的超高速撞击石灰岩靶实验研究成果，研究了开坑深度、直径和体积随撞击初速、弹靶密度、靶体孔隙率等参数的变化规律。Antoun 等[20]、Wünnemann 等[21]、Kenkmann 等[22]、邓国强等[23]针对开坑机理进行了数值模拟研究，给出了开坑直径无量纲数与靶体材料强度无量纲数的关系。

另外，也有长杆弹超高速侵彻半无限混凝土靶方面的研究工作。Dawson 等[24]开展了钨合金、铝长杆弹以速度1.5～2.2 km/s 贯穿中厚度混凝土靶的实验，记录了靶面开坑形貌（见图1），并采用CTH 对实验进行了数值模拟。Gold 等[25-26]开展了铜、钽长杆弹以速度1.475～1.875 km/s 侵彻混凝土厚靶的实验，并分别采用固体材料和多孔材料状态方程计算超高速侵彻条件下混凝土材料的力学响应，结果表明采用多孔材料状态方程的计算结果与实验结果更吻合。钱秉文等[27]开展了钨合金短圆柱弹体以速度1.8～4.0 km/s 撞击混凝土靶的实验（见图2），并基于实验结果对超高速撞击条件下开坑特性进行了量纲分析，得到了开坑体积和开坑直径的计算公式。Kong 等[28]开展了45 钢圆柱弹体以速度0.510～1.855 km/s撞击砂浆靶的实验，结果显示的规律性与钱秉文等[27]的一致，并采用侵蚀弹体模型对侵彻深度、剩余弹体长度等进行了计算。

图1 钨合金长杆弹和混凝土靶的破坏[24]Fig.1 Tungsten long rod and failure of concrete target[24]

综上所述，目前对长杆弹超高速侵彻混凝土靶的开坑研究仍处于初步阶段，相关实验数据还不充分。本文中，参照文献[25]中的实验研究，开展TU1 无氧铜和Q235 钢长杆弹超高速侵彻半无限混凝土靶的实验，结合以往文献和本文实验的数据对长杆弹超高速侵彻半无限混凝土靶的开坑直径和开坑体积进行量纲分析，基于弓形开坑截面几何关系获得开坑深度的预测公式。

1 侵彻实验

利用二级轻气炮发射平台，精确控制长杆弹超高速正侵彻混凝土靶，进行不同初始速度、不同弹靶材料的对比实验。在侵彻过程结束后，测量开坑直径和深度、侵彻深度，为开坑尺寸量纲分析提供实验数据。向弹洞灌装明胶，待明胶冷却凝固后，剖开靶体测量弹洞半径，得到最终侵彻深度和弹洞半径等实验数据。

1.1 弹体、靶体参数

文献[25]中，长杆弹以初速1.626～1.875 km/s 超高速侵彻C35 混凝土靶，铜长杆弹长径比为14.6、10.8。为了对比和补充，本文实验中采用长杆弹长径比也为14.6、10.8，弹体初速为1.8～2.4 km/s，弹体材料分别为TU1 无氧铜和Q235 钢，弹体的结构和材料参数见表1。长杆弹实物如图3 所示。

表1 弹体的结构和材料参数Table 1 Geometric and material parameters of long rods

图3 长杆弹实物Fig.3 Photo of long rods

靶体为骨料尺寸不超过5 mm 细骨料素混凝土圆柱体，尺寸为 ∅ 800 mm×600 mm，外层用厚2 mm 钢筒包裹以提供围压。实测混凝土单轴抗压强度分别为26.5、42.1 MPa，靶体实物如图4 所示。

图4 混凝土靶体实物Fig.4 Photos of concrete targets

1.2 发射和测试

实验加载装置为 ∅ 30 mm 二级轻气炮，在出炮口处经磁测速系统和激光遮断测速系统（all fiber optical beam breakout, OBB）测量弹体初速。长杆弹由弹托加底推构成，外部由聚碳酸酯（PC）包裹，长杆弹与底部聚乙烯（PE）底座之间加装HR2 钢片底推板，防止加载过程中应力过大导致的聚乙烯（PE）底座破碎。发射结构、尺寸如图5 所示，实物如图6 所示。

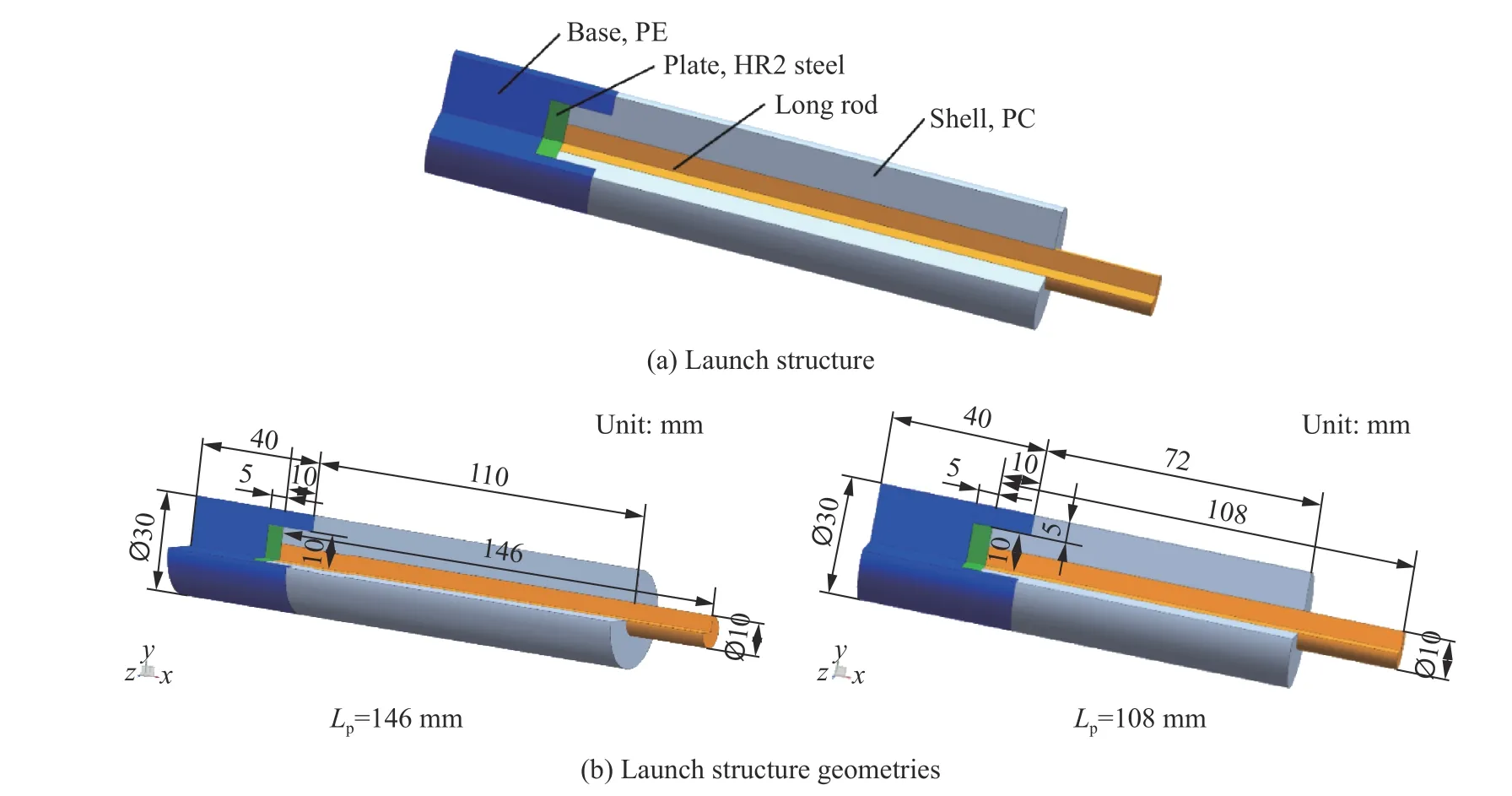
图5 发射结构及其尺寸Fig.5 Launch structures and their geometries

图6 发射结构实物Fig.6 Photos of launch structures

为了准确说明弹体飞行时的上下俯仰和左右偏转状态为稳定飞行，同时在竖直和水平方向采用激光遮断测速系统OBB 测量弹体初速，二者数值相同则说明弹体出炮口为正侵彻方向。OBB 测速装置中的前后两组探头间距100 mm，每组的两对探头均水平和竖直放置，每对探头包括一个发射探头和一个接收探头。在实验过程中，长杆弹头部经过探头中间位置时会对光路产生遮断，使接收探头无法接收激光束，此时接收探头连接的示波器记录遮断信号。然后，读取示波器上记录的竖直和水平两个方向前后两组遮断信号时间差，换算为发射速度，即弹体初速。激光遮断测速系统OBB 如图7～8 所示。采用闪光照相系统拍摄弹体出炮口飞行姿态，受拍摄窗口尺寸限制，只能拍摄从弹体头部开始约7 cm 长度的弹体飞行过程。X 射线结果如图9 所示。

图7 OBB 测速装置Fig.7 OBB velocity measure device

图8 测速装置实物Fig.8 Photo of velocity measure device

图9 X 射线照片Fig.9 X-ray flash photo

靶室内部已有对正炮口的放置平台，实验中将靶体置于特制靶架，并通过靶架下部螺栓限位孔可微调靶体位置使靶面垂直于出炮口，靶架实物和靶体放置情况分别如图10～11 所示。实验后，回收弹洞中剩余弹体发现，6 发实验中的长杆弹均全部侵蚀，弹洞底部仅存在部分弹体碎屑，如图12 所示。其中，弹体碎屑一侧表面光滑，另一侧表面粘连了混凝土材料，表明弹体头部出现了蘑菇头变形。随后，取出靶体，采用卷尺测量靶面开坑直径、开坑深度，并计算开坑体积，如图13 所示。向弹洞内灌装明胶，明胶冷却48 h 成型后，剖靶观测开坑底部截面和弹洞段的弹洞直径和侵彻深度，如图14 所示。

图10 靶架实物Fig.10 Photo of target holder

图11 靶体放置Fig.11 Photo of target placement

图12 实验回收的弹体碎渣Fig.12 Recovered debris of long rod after experiment

图13 靶面开坑Fig.13 Crater of target surface

图14 剖靶后的开坑和弹洞截面Fig.14 Crater and hole after cutting target

1.3 实验结果

共进行了6 发实验，弹体初速范围为1.8～2.4 km/s。实验条件和结果见表2～3。由图14 和图2(b)可以看出，长杆弹超高速侵彻混凝土靶的靶体破坏主要包括弓形截面开坑和柱形弹洞两个部分。弓形截面开坑部分的开坑直径较大，为弹体直径的约60 倍；开坑深度也相对较深，为弹体直径的12～17 倍，达到侵彻深度的1/3～1/2，而动能弹中低速侵彻混凝土靶时开坑深度仅为两倍弹体直径。

由实验结果可以看出，弹体完全侵蚀，弹体头部出现较大变形，符合半流体侵彻特征。另外，实验4 弹洞直径在弹洞末段出现了减小，且在弹洞底部还有几乎没有变形的HR2 钢底推片，表明实验4 出现了HR2 钢底推片的随进侵彻。与其他实验结果比较，实验4 的弹洞直径实验结果在弹洞直径几乎没有变化的部分具有良好的规律性。还有，由于本文实验中未对发射组件进行脱弹托处理，使开坑尺寸明显大于脱壳弹体状况的，对它的数据处理方法见第2 节。

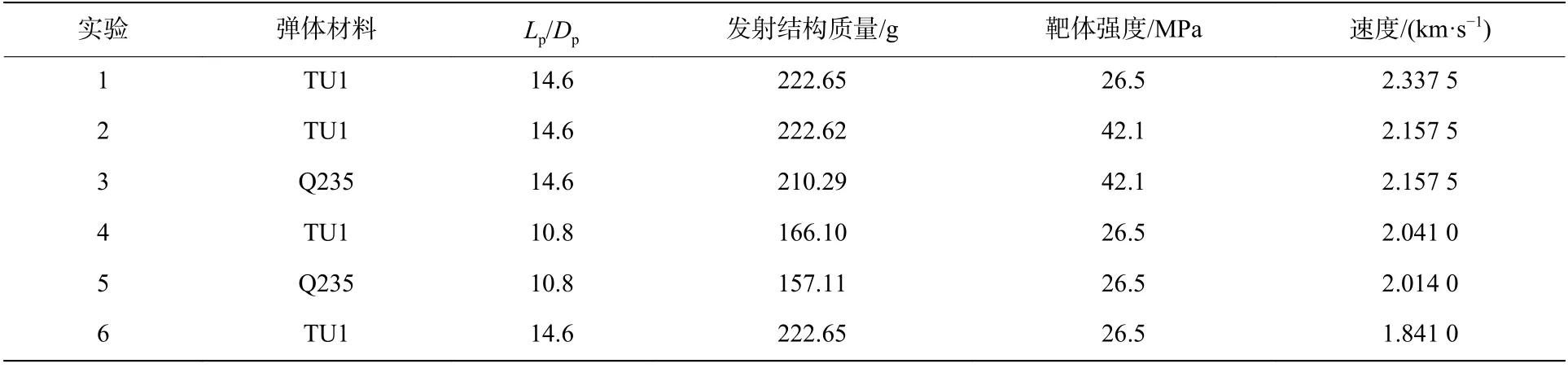
表2 长杆弹超高速侵彻半无限混凝土靶的实验条件Table 2 Experimental conditions of long rods hypervelocity penetration into semi-infinite concrete targets

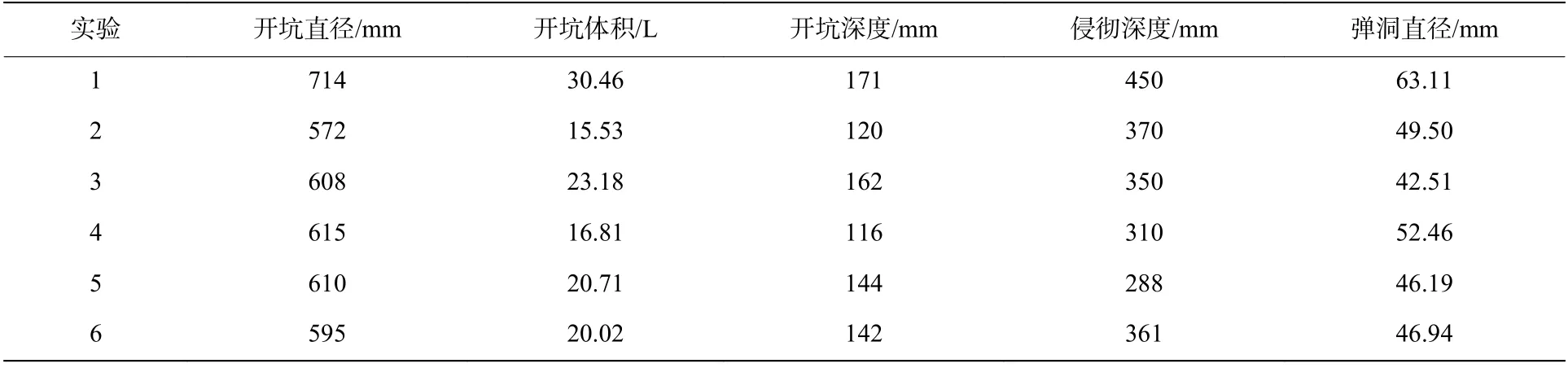
表3 长杆弹超高速侵彻半无限混凝土靶的实验结果Table 3 Experimental results of long rods hypervelocity penetration into semi-infinite concrete targets

1.4 与其他文献实验对比

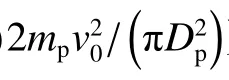
2 开坑效应

2.1 开坑尺寸量纲分析

由于混凝土材料为脆性材料，在长杆弹超高速撞击混凝土时，靶面产生了明显的开坑现象。而长杆弹超高速侵彻混凝土靶开坑过程包含了复杂的物理机制，在理论上难以建立相应的分析模型。量纲分析作为探讨科学规律、解决科学和工程问题的一个有效工具，可用来对长杆弹超高速侵彻混凝土靶的开坑形貌开展分析，探讨开坑尺寸和弹靶相关参数之间的关系。现有文献中长杆弹超高速侵彻混凝土靶的开坑深度数据很少，本文实验数据点也相对较少，因此，无法直接对开坑深度进行量纲分析。本文中，对开坑尺寸的量纲分析主要针对开坑直径和开坑体积两方面进行。

长杆弹超高速侵彻混凝土靶的开坑过程涉及很多弹靶参数，包括：弹体的长度Lp、直径Dp、质量mp、密度ρp、强度σp、弹性模量Ep、剪切模量Gp，靶体的密度ρt、直径Dt、厚度Ht、抗压强度fc、弹性模量Et、剪切模量Gt、抗拉强度σct、抗剪强度σst，弹体的碰撞初速v0、倾角α、攻角β 等。

本文实验中，靶体直径和厚度足够大且外围采用钢板包裹提供围压，因此可将靶体等效为半无限靶体，可以略去Dt和Ht两个物理量；剪切模量和强度相关，且不同强度的钢弹性模量相差不大，因此可略去Ep、Gp、Et、Gt、σct、σst等物理量；本文实验中，所有靶体的破坏效果均接近图1 中的情况，由实验后侵彻弹道均呈直线的结果，可知本文实验为正侵彻，因此可略去α 和β 两个物理量；弹体质量是和弹体密度、长度、直径相关联的量，因此可略去物理量ρp。本文实验中，为保证长杆弹的飞行稳定，没有对它作脱弹托处理。碰撞开始时，只有长杆弹与靶面发生碰撞，而聚碳酸酯包裹层并没有与靶面接触，因此，在对开坑过程进行量纲分析时，将弹体质量取为发射结构总质量，弹体直径仍取长杆弹直径。综上，靶体开坑直径Dc和开坑体积Vc与各参数的关系可以写成：

从上述两式可以看出，所有出现的物理量的量纲只涉及到L、M 和T 等3 类量纲。因此，根据Π 定理，取Dp、fc、ρt为量纲基本量。超高速侵彻条件下，材料更接近流体、弹靶强度影响明显变小，惯性效应（密度、速度）是主要影响因素，因此，可以忽略混凝土的不均匀性、黏性和应变率效应和弹靶强度之比的影响。将其他物理量无量纲化，整理可得到：

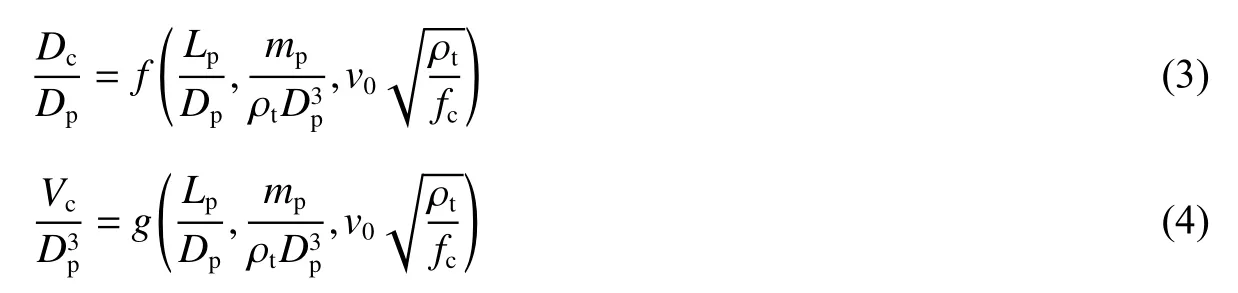
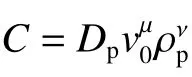
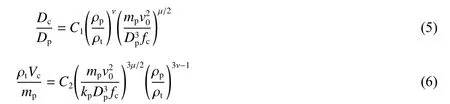
结合本文和文献[24-25,27-28]中的实验数据，对式(7)～(8)进行拟合（见图15～16），可得：

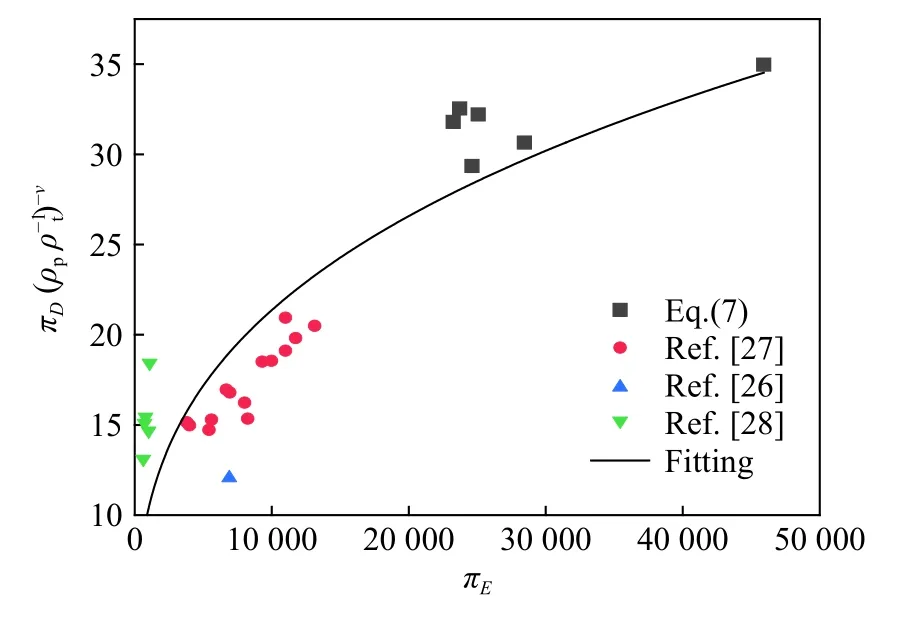
图15 开坑直径与动能的实验数据和拟合Fig.15 Fitting of crater diameter and kinetic energy experimental data

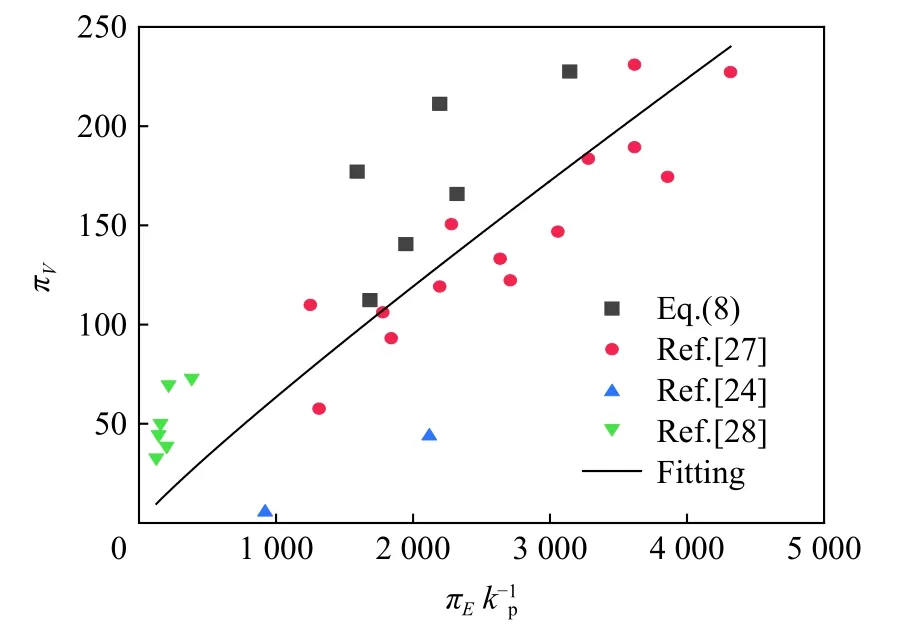
图16 开坑体积与动能的实验数据和拟合Fig.16 Fitting of crater volume and kinetic energy experimental data

对比式(5)～(6)和拟合结果式(9)～(10)可知，待定系数 µ 分别为0.78 和0.61，二者的平均值为0.69，即µ≈2/3。由此可知，长杆弹超高速侵彻混凝土靶的开坑过程主要受弹体动能影响，并可在以后的分析中令µ=2/3，以使分析过程更简便。

2.2 开坑深度预测公式

上述量纲分析结果表明，可取µ=2/3、ν=1/3 对开坑尺寸进行分析。因此，将µ=2/3、ν=1/3 代入式(5)～(8)，可得开坑直径和开坑体积的预测公式为：

依据式(11)～(12)对实验数据进行处理，拟合结果如图17～18 所示，开坑直径和开坑体积的具体预测公式为：

由拟合结果可知，无量纲开坑直径与发射组件无量纲动能的立方根成正比，无量纲开坑体积与发射组件无量纲动能成正比。

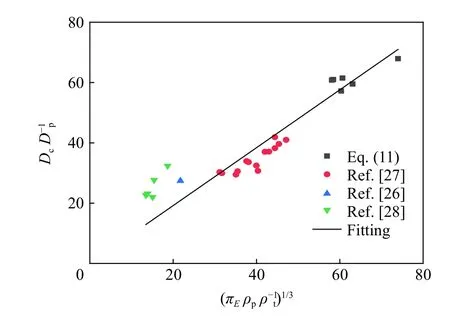
图17 开坑直径的拟合Fig.17 Fitting of crater diameter

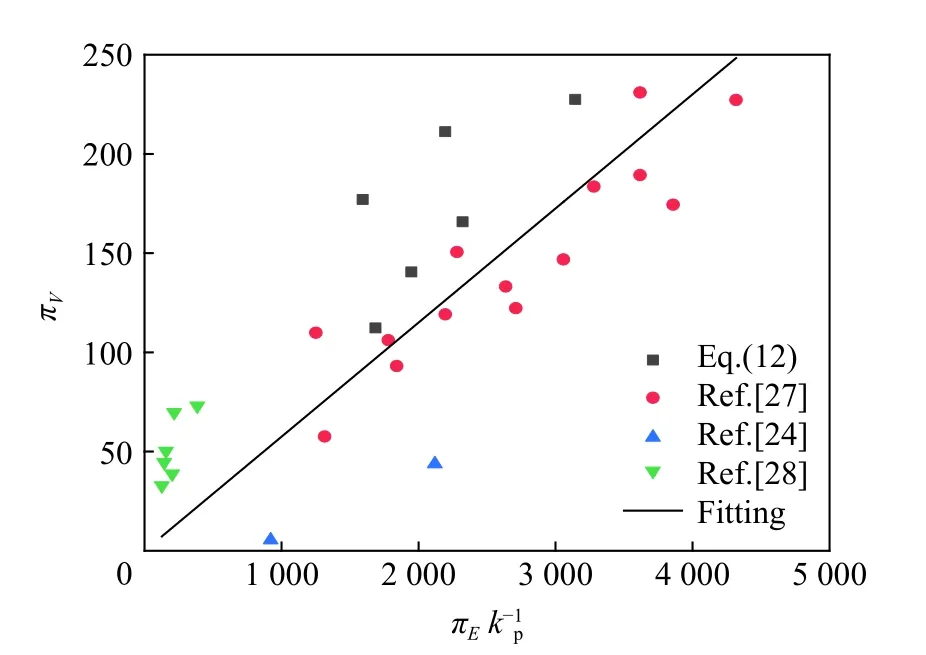
图18 开坑体积的拟合Fig.18 Fitting of crater volume

混凝土材料的非均匀性较强，且实验中弹体直径较小，实验结果中对开坑尺寸进行无量纲化处理会带来较大实验误差，因此实验结果数据比较分散，但是整体结果还是具有一定的规律性，开坑直径和开坑体积的预测公式具有一定的预测价值。

从剖靶截面形貌(见图14)和文献[27]中通过CT 扫描得到的开坑截面形貌(见图2(b))可以看出，超高速侵彻混凝土靶的开坑截面形貌可以近似为弓形。根据弓形开坑截面的形貌几何关系，利用上述开坑直径和开坑体积的预测公式可计算开坑深度。开坑截面形貌如图19 所示。

以坑底中心为原点构建直角坐标系，Rb是弓形弧线半径，Hc是开坑深度，则开坑截面的右半部轮廓曲线为：

对式(15)积分，可得到开坑体积：

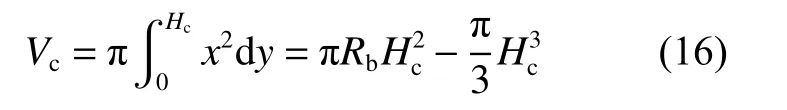
由几何关系可知：

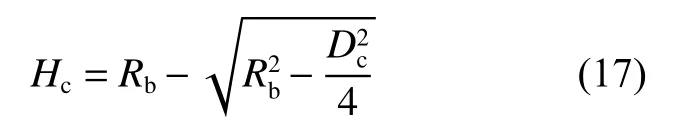
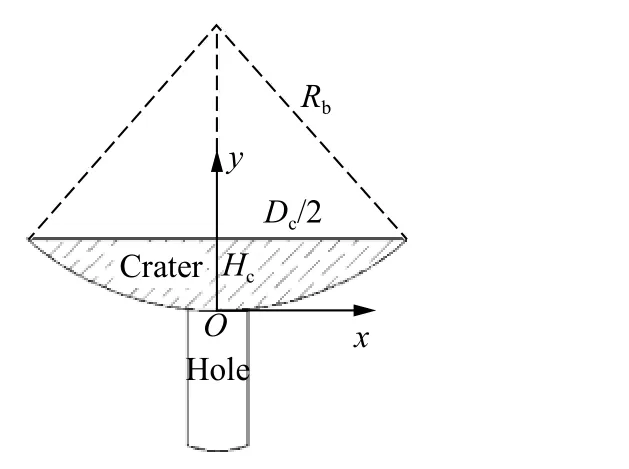
图19 弓形开坑截面Fig.19 Section of bow-shaped crater

将式(17)代入式(16)，可得：

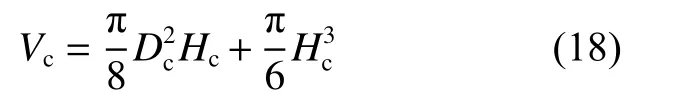
解方程可得开坑深度预测公式：

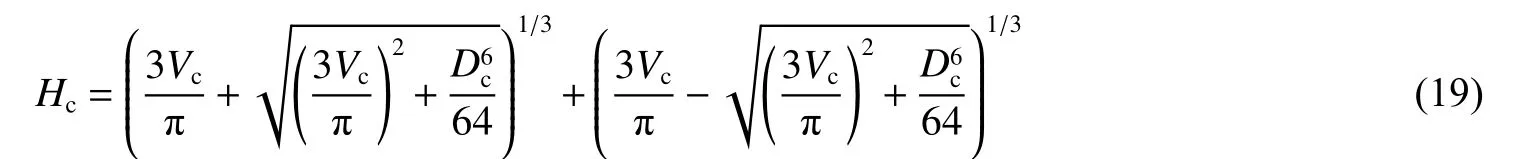
利用式(19)对本文实验开坑深度进行预测，计算结果和实验结果对比见表4，其中另6 个实验数据取自文献[28]中倾角小于3°的侵蚀弹体对应实验。本文实验和文献[28]中的计算结果小于实验结果，这是因为在对开坑实验数据进行拟合时，本文实验和文献[28]中开坑体积明显大于拟合结果，而开坑直径与拟合结果相差不大，导致了采用开坑深度预测公式得到的结果小于实验结果，但它仍然具有一定的预测价值。

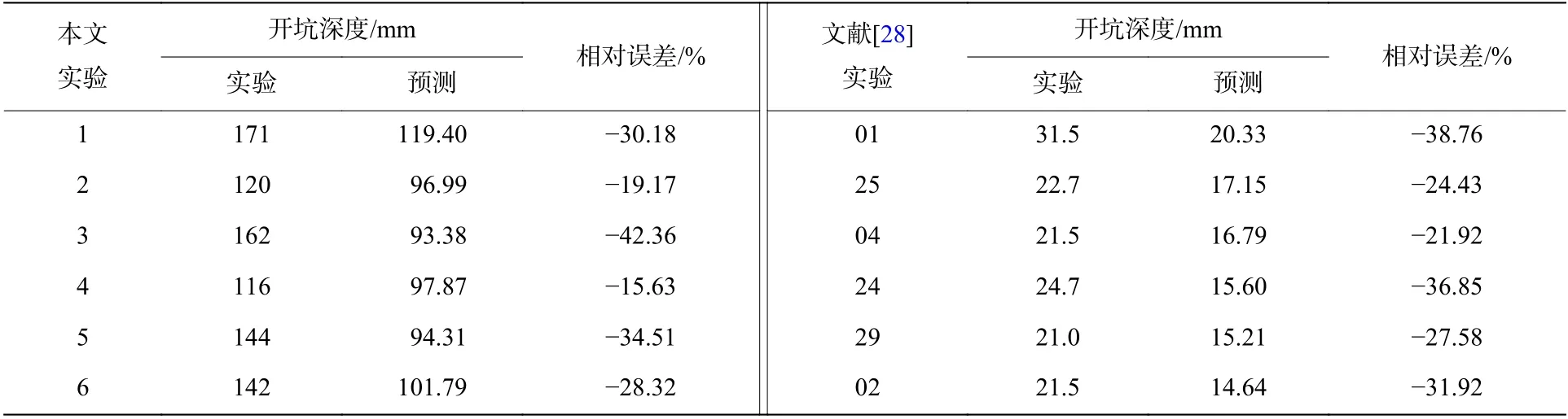
表4 开坑深度预测结果Table 4 Prediction of crater depths

3 结 论

对比文献[25] 中相关实验，开展了初速1.8～2.4 km/s 的TU1 铜、Q235 钢长杆弹超高速正侵彻26.5、42.1 MPa 混凝土靶的实验，基于本文实验和以往文献中相关实验结果对侵彻机制进行了说明，对混凝土靶面的开坑直径和开坑深度进行了量纲分析，将开坑截面近似为弓形，给出长杆弹超高速侵彻混凝土靶时开坑深度预测公式。主要结论如下。

（1）长杆弹超高速侵彻混凝土靶过程中，弹体长度发生严重的长度缩短，直至最后完全侵蚀，弹洞半径明显大于弹体半径，说明侵彻过程中弹体出现了明显的蘑菇头变形，属于半流体侵彻机制。弹体长度是影响侵彻深度的最主要参数，侵彻深度随弹体长度和密度的增大而增大，受弹体强度影响不大。

（2）相比于中低速侵彻条件下靶面锥形漏斗状开坑，长杆弹超高速侵彻条件下混凝土靶的开坑截面近似为弓形。无量纲开坑体积与发射组件无量纲动能成正比。靶面开坑直径较大，为长杆弹直径的约60 倍，无量纲开坑直径与发射组件无量纲动能的立方根成正比。

（3）长杆弹超高速侵彻混凝土靶的靶面的开坑深度为弹体直径的12～17 倍，达到总侵彻深度的1/3～1/2，明显大于动能弹中低速侵彻混凝土靶条件下仅有两倍弹体直径的开坑深度。本文开坑深度预测公式中考虑了以往文献中不同弹靶条件的实验结果，虽然得到的结果小于实验结果，但它仍然具有一定的预测价值。

对中国工程物理研究院流体物理研究所在实验测试中的大力支持和帮助和郝龙助理研究员对实验研究的帮助和指导，表示感谢。