考虑钢筋锈蚀的钢筋混凝土矩形梁恢复力模型研究
2020-10-09郑淏郑山锁贺金川张艺欣尚志刚
郑淏,郑山锁,2,贺金川,张艺欣,尚志刚
(1.西安建筑科技大学土木工程学院,陕西西安,710055;2.西安建筑科技大学结构工程与抗震教育部重点实验室,陕西西安,710055;3.西安建筑科技大学建筑设计研究院,陕西西安,710055)
我国海岸线漫长,近海城市众多,该类近海大气环境下的RC(reinforced concrete)建筑结构在长期服役过程中耐久性逐步退化,其中最主要的原因是其表面遭受氯化物侵蚀,引起内部钢筋锈蚀,进而影响整个结构安全[1-2]。我国地震灾害严重、地震分布广,其中近海地区强震活跃[3-4],因此,处于近海大气环境下的RC建筑结构也位于地震设防区[5]。RC梁是RC建筑结构的主要受力构件,受氯化物侵蚀导致钢筋锈蚀后其力学性能劣化,会直接影响整体结构的抗震性能[6]。目前,国内外学者研究了锈蚀RC 梁的抗震性能。TORRESACOSTA 等[7]通过试验研究了锈蚀RC 梁纵向受力钢筋截面损失与抗弯承载力之间的关系,发现钢筋表面最大坑蚀深度是造成梁抗弯承载力降低的最主要因素;DU 等[8]研究了钢筋锈蚀对混凝土梁破坏模式及延性性能的影响,发现钢筋锈蚀不仅降低了梁的抗弯承载力,而且改变了其破坏模式,同时降低了其延性性能;RODRIGUEZ 等[9]总结与分析了锈蚀混凝土梁的研究进展;VAL[10]通过2种加速腐蚀方法,研究了钢筋锈蚀对RC梁抗弯强度和抗剪强度的影响;TACHIBANA等[11]通过试验和有限元分析研究了钢筋锈蚀对RC梁力学性能的影响;袁迎曙等[12]对锈蚀RC 梁进行了试验研究,提出了锈蚀钢筋混凝土梁性能退化模型。然而,这些研究大多仅采用试验方法分析了钢筋锈蚀对结构力学性能的影响,而未建立考虑锈蚀劣化的RC梁恢复力模型。恢复力表示构件或结构在外力卸载后恢复其原始形状的能力。在过去的大半个世纪内,地震工程界基于大量RC试件的拟静力试验与恢复力特性研究,提出了多种恢复力模型。CLOUGH[13]提出了考虑再加载刚度退化的退化双线性模型;TAKEDA 等[14]改进了CLOUGH 模型,考虑了卸载刚度退化;PARK等[15]采用三折线骨架曲线,提出了一种考虑强度衰减、刚度退化以及捏缩效应的恢复力模型;朱伯龙等[16]利用统计回归的方法,建立了包含下降段的四折线骨架曲线和在滞回规则中考虑卸载刚度退化的恢复力模型。不过,现有恢复力模型大多是基于未锈蚀构件,没有考虑钢筋锈蚀劣化对构件力学性能的影响。为此,本文基于6 榀不同锈蚀程度和配箍率的RC矩形梁试件拟静力试验结果,建立用于计算锈蚀劣化RC矩形梁骨架曲线的三折线模型;从能量耗散的角度出发,引入循环退化指数βi描述试件在往复荷载作用下由于累积损伤效应导致的强度和刚度退化,进而建立考虑钢筋锈蚀的RC矩形梁恢复力模型;最后,结合拟静力试验结果,验证所建恢复力模型的有效性。
1 试验概况
1.1 试件设计与制作
参考文献[17],设计并制作6 榀剪跨比λ为5.47 的RC矩形梁,以锈蚀程度和配箍率作为变化参数。试件的几何尺寸和配筋情况如图1所示。梁截面的宽×高为150 mm×250 mm,长度为1 300 mm,混凝土保护层厚度为7.5 mm,受拉和受压纵筋均分别采用3B16(HRB335钢筋),箍筋为A6@60/80/100(HPB300 钢筋)。各试件的设计参数见表1。

图1 试件尺寸及配筋Fig.1 Dimensions and reinforcements of specimens
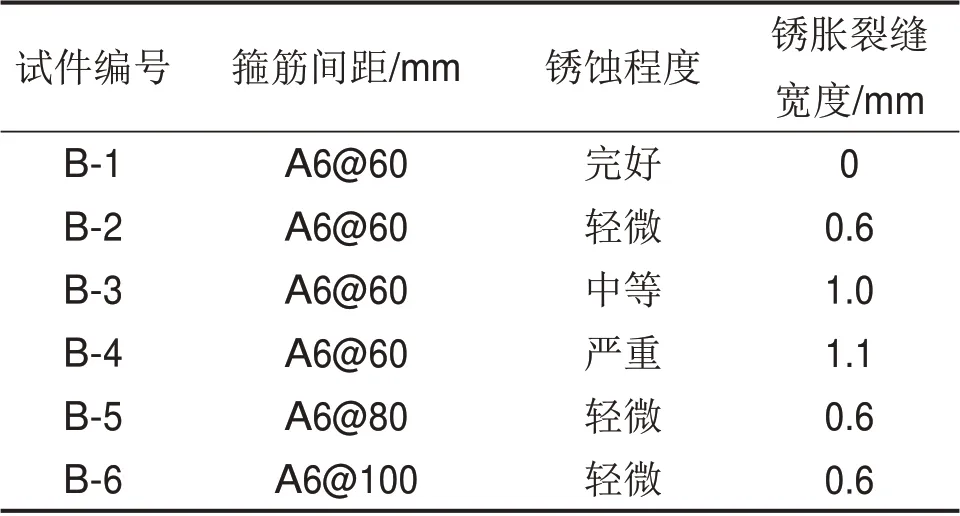
表1 试件设计参数Table 1 Design parameters of specimens
1.2 材料性能
本试验采用P.O 42.5R 级水泥,配制强度等级为C30的混凝土。浇筑RC梁的同时,制作若干边长为150 mm的标准立方体试块,进行混凝土力学性能试验,测得混凝土立方体抗压强度为24.6 MPa,轴心抗压强度为18.0 MPa,弹性模量为2.85×104MPa。此外,进行钢筋力学性能试验,结果如表2所示。
1.3 加速腐蚀试验方案
目前,国内外学者研究钢筋锈蚀对构件力学性能的影响,大多采用恒电流通电的方法加速钢筋锈蚀[18-20]。袁迎曙等[20]指出采用恒电流通电法的钢筋锈蚀电化学机理及锈蚀结果均与自然环境下的不符。
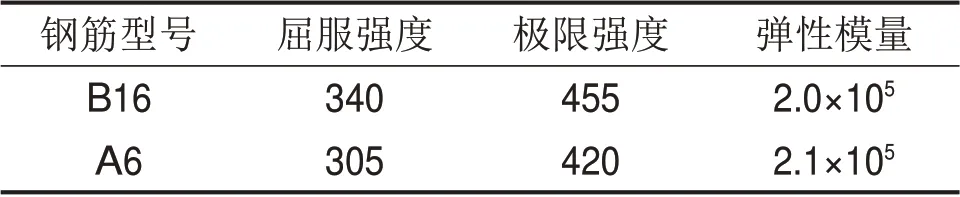
表2 钢筋力学性能Table 2 Mechanical properties of reinforcements MPa
因此,为准确揭示近海大气环境下钢筋锈蚀对RC梁抗震性能的影响,依托西安建筑科技大学人工气候环境室,采用与自然环境下钢筋锈蚀机制相同的人工气候环境法对RC梁试件进行加速腐蚀试验,模拟近海大气环境中的气候作用过程。
将试件B-1作为对比试件,不进行加速锈蚀试验。为了尽早破坏钢筋钝化膜,其余试件在浇筑过程中掺加水泥质量分数为5%的NaCl[1],养护结束后,调节人工气候环境室内的温度和湿度(温度为45 ℃,湿度为90%),将试件转移至环境室进行加速锈蚀试验。
为模拟自然环境下浸润→潮湿→干燥的气候循环作用过程,采用干(烘干)—湿(喷淋盐雾)循环方式加速钢筋锈蚀。其中,盐雾为质量分数为5%的NaCl 溶液,喷淋盐雾阶段每1 h 为1 个周期(喷淋20 min→间歇40 min),即每个循环喷淋4 个周期。干湿循环示意如图2所示。
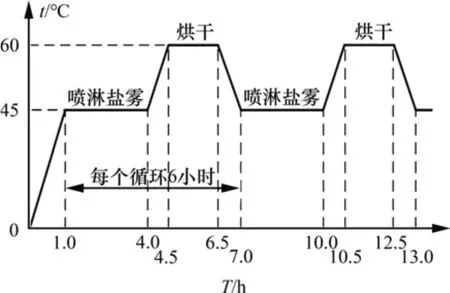
图2 干湿循环示意图Fig.2 Schematic diagram of dry-wet cycle
1.4 试验加载装置和制度
本试验采用位移控制加载,加载装置如图3所示。在试件达到屈服状态之前,采用较小级差进行加载,获得较准确的试件屈服时对应的水平荷载与位移特征值;加载至屈服状态后,以屈服时水平位移的倍数为级差进行加载,每级循环3 次;当试件水平承载力下降至水平峰值荷载的85%之后或试件破坏明显而不能继续承受水平荷载时,停止试验。
2 试验结果
2.1 纵筋锈蚀率
干伟忠等[19]采用锈胀裂缝宽度表征试件的锈蚀程度。基于其大量试验结果,本文设定了不同锈蚀程度的沿纵筋方向锈胀裂缝宽度,如表1所示。在加速腐蚀试验过程中,定期观测试件表面锈胀裂缝发展情况,以控制实际锈蚀程度。其中,所采用的裂缝观测仪精度为0.01 mm,量程为0~10.00 mm,并取各试件裂缝宽度平均值作为其锈胀裂缝宽度,当达到设计裂缝宽度时,停止对相应试件的腐蚀。加速腐蚀试验完成后,截取各试件的纵筋,并按照文献[20]中方法计算其实际锈蚀率,计算结果见表3。
2.2 滞回曲线
根据试验测得6榀试件的荷载-位移滞回曲线,如图4所示。由图4可见:试件的滞回曲线具有如下特点。
1)对比配箍率相同而锈蚀程度不同的试件B-1,B-2,B-3 和B-4,在屈服荷载之前,各试件滞回曲线较为类似,加卸载曲线基本重合,残余变形较小,但在同一级加载位移下,锈蚀试件的强度退化较未锈蚀试件更为明显;在屈服荷载之后,随着钢筋锈蚀程度增大,各试件的强度和刚度退化逐步加重,屈服平台段变短,滞回环的面积减小,捏拢现象更加明显,表明RC 梁的承载力、变形和耗能能力均随着锈蚀程度增大而不断退化。
2)对比锈蚀程度相同而配箍率不同的试件B-2,B-5和B-6,在试件屈服之前,各试件滞回曲线基本重合;在试件屈服之后,随着配箍率减小,各试件承载力降低,滞回环稳定性变差,包围的面积减少。
2.3 骨架曲线及特征参数
本文采用屈服弯矩法确定骨架曲线屈服点,取峰值荷载下降至85%的荷载作为极限荷载[21],极限位移对应于极限荷载。以延性系数μ[22]表征试件的延性性能,其计算公式如下:
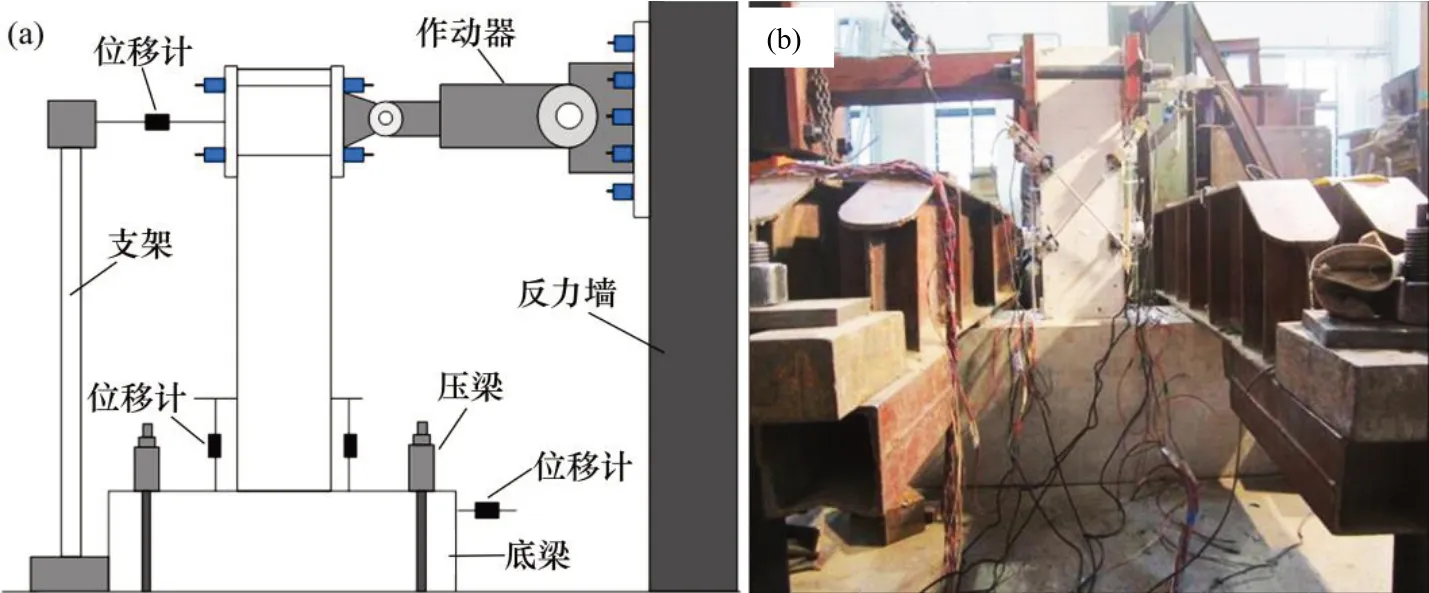
图3 试验加载装置Fig.3 Experimental equipment for loading
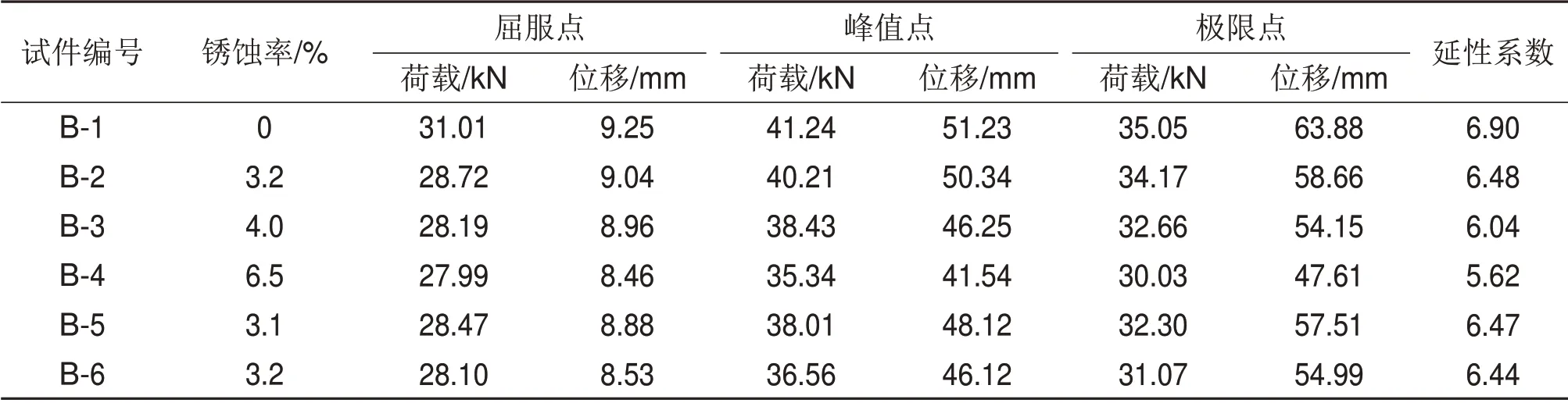
表3 试件特征参数Table 3 Characteristic parameters of specimens

式中:Δu和Δy分别为试件的极限位移和屈服位移。
图5所示为基于滞回曲线绘制各试件的骨架曲线。由图5(a)可见:随着钢筋锈蚀程度增加,骨架曲线平直段逐渐变短,曲线下降段逐步变陡峭,试件屈服荷载、峰值荷载和极限荷载均逐渐减小,延性系数降低,说明钢筋锈蚀对RC梁承载力和延性均产生了不利影响。由图5(b)可见:随着配箍率减小,骨架曲线逐渐降低,试件各特征点的荷载逐渐减少,极限位移逐渐变小。
3 恢复力模型的建立
3.1 骨架曲线
本文建立恢复力模型时,骨架曲线选用考虑负刚度段的三折线型模型。对比图5所示的各试件试验骨架曲线可知,锈蚀试件与完好试件的骨架曲线形状类似,但由于钢筋锈蚀导致各特征点发生变化。因此,锈蚀RC梁试件骨架曲线亦采用三折线型模型,同时考虑钢筋锈蚀对其力学性能的影响,如图6所示。
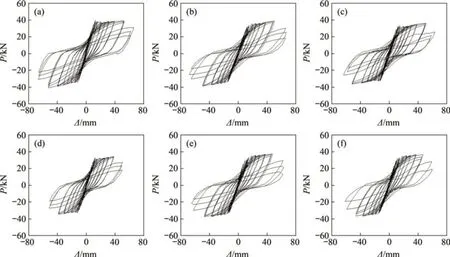
图4 试件滞回曲线Fig.4 Hysteresis curves of specimens
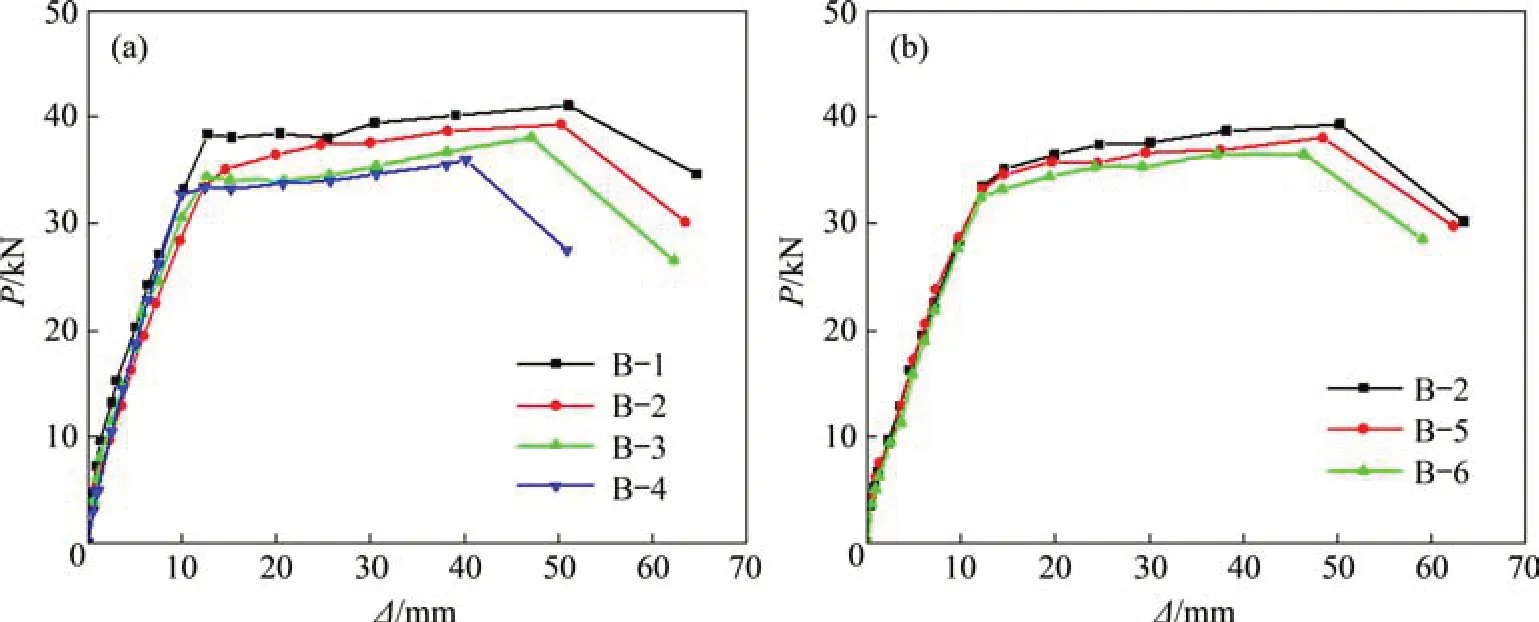
图5 试件骨架曲线Fig.5 Skeleton curves of specimens

图6 三折线型骨架曲线Fig.6 The skeleton curve of three fold line
3.1.1 完好试件骨架曲线特征参数确定
确定完好构件恢复力模型骨架曲线需要6个特征点参数:屈服荷载Py'、屈服位移Δy'、峰值荷载Pp′、峰值位移Pp′、极限荷载Pu'和极限位移Δu',如图6所示,各特征点参数的确定过程叙述如下。
1)屈服荷载Py'。屈服荷载与梁端部截面屈服弯矩关系如下:

式中:L为梁的计算高度,即水平加载点至梁端部的距离;M′y为屈服弯矩,按下式计算[23]:
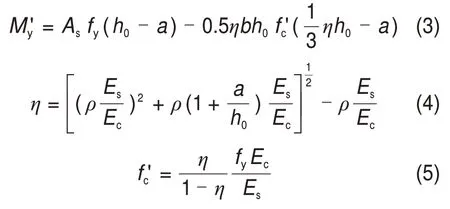
式中:As为受拉钢筋截面面积;fy为钢筋屈服强度;h0为截面有效高度;a为受拉钢筋中心至截面边缘距离;η为混凝土受压区高度系数;b为截面宽度;ρ为受拉钢筋配筋率;Ec和Es分别为混凝土和钢筋的弹性模量;f'c为截面屈服时混凝土的最大压应力。
2)屈服位移Δy'。基于文献[24]的塑性铰理论,计算RC梁各受力状态的特征位移。综合考虑弯曲变形、剪切变形和受拉纵筋在节点锚固区的伸长引起梁端附加转动对梁端变形的贡献,采用下式计算梁端的屈服位移:
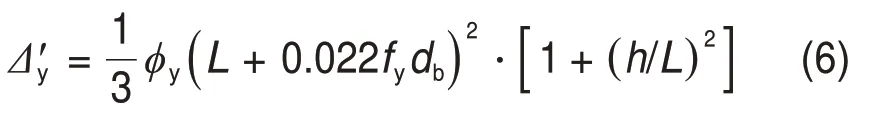

式中:φy为屈服状态截面曲率;db为纵筋直径;h为截面高度;ky为屈服时的中性轴高度;ρ'为受压钢筋配筋率;δ'=h'/h;h'为受压区边缘至受压钢筋中心的距离。
3)峰值荷载Pp′为

式中:fc为混凝土立方体抗压强度。
4)峰值位移Δp'为
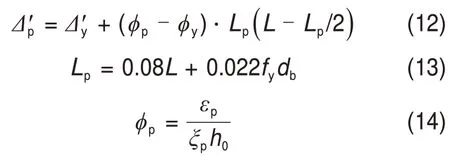
式中:φp为峰值状态截面曲率;Lp为塑性铰长度,按式(13)计算[25];εp为峰值状态混凝土压应变,取0.004[24];ξp为峰值状态截面相对受压区高度,取0.082[24]。
5)极限荷载Pu'为

6)极限位移Δu'为

式中:φu为极限状态截面曲率;εcu为极限状态混凝土压应变;ξu为极限状态截面相对受压区高度;Ke为箍筋有效约束系数;λv为配箍特征值;wi'为相邻纵筋的净间距;bcor和hcor分别为约束截面的宽度和高度;s'为箍筋的净间距;ρcc为纵筋相对于约束截面的配筋率。
此外,还应考虑纵筋破坏[24]:

式中:εsu为纵筋极限应变;h0,cor为核心区截面有效高度。取式(17)和式(21)的较小值作为极限状态截面曲率。
3.1.2 锈蚀试件骨架曲线特征参数确定
对上述试验数据进行回归分析,得到锈蚀RC梁试件骨架曲线特征点参数与钢筋锈蚀率、配箍率和未锈蚀梁试件特征点参数之间的关系式。
1)屈服荷载Py和屈服位移Δy:
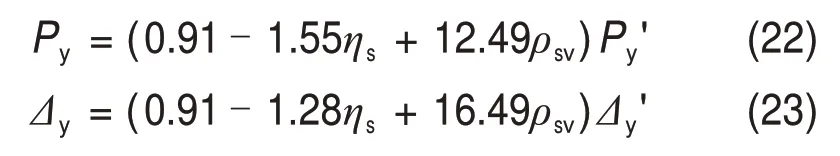
式中:ηs为纵筋锈蚀率;ρsv为配箍率。
2)峰值荷载Pp和峰值位移Δp:

3)极限荷载Pu和极限位移Δu:

3.1.3 骨架曲线特征参数验证
采用上述建立的计算模型计算各试件骨架曲线的特征点,并与试验结果对比,如图7所示。由图7可见:建立的锈蚀RC 梁骨架曲线三折线模型在计算特征点参数时误差总体较小,计算值与试验值较吻合。因此,该模型对不同锈蚀程度和配箍率的RC 梁骨架曲线特征参数计算有较好的适用性。
3.2 滞回规则
由试验结果可知,锈蚀试件的滞回曲线形式与完好试件的基本相同,仅因为钢筋锈蚀导致其各项力学性能衰减。基于此,为建立精度较高且简单实用的恢复力模型,建立锈蚀RC梁恢复力模型时,其滞回规则与完好试件的相同,并引入基于能量耗散的循环退化指数βi,考虑强度衰减和刚度退化。
3.2.1 循环退化指数
本文基于能量耗散考虑试件强度及刚度退化[26],其基本假定是试件本身滞回耗能能力恒定,不考虑其加载历程的影响。
试件第i次循环退化速率由循环退化指数βi确定,按下式计算[26]:
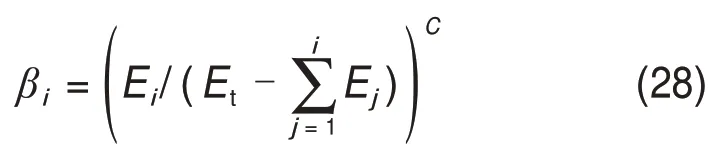
式中:Ei为试件第i次循环时的滞回耗能;C为控制循环退化速率的参数,取1.5[26];Et为试件自身滞回耗能能力,计算式[27]为
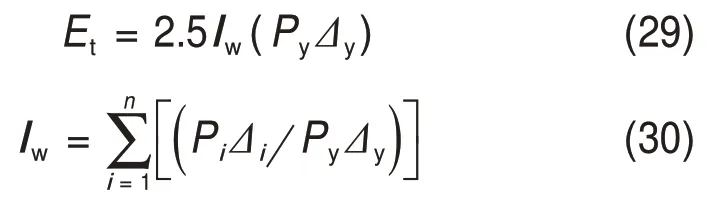
式中:Py和Δy分别按式(22)和(23)计算;Iw为试件的功比系数;Pi和Δi分别为第i次循环时卸载点的荷载和位移。
3.2.2 基本强度退化

图7 骨架曲线验证Fig.7 Verification of skeleton curves
图8所示为滞回规则示意图。基本强度退化表征屈服后再加载段的屈服强度退化和强化段刚度退化,如图8(a)所示,其中,屈服强度的退化规则由下式计算:
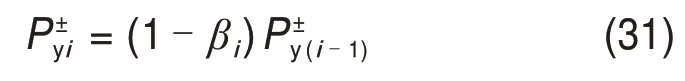
式中:为第i次循环加载后发生性能退化的屈服强度;“+”表示正向加载,“-”表示反向加载。
强化段刚度退化规则按下式计算,

式中:为第i次循环加载后发生性能退化的硬化刚度。
3.2.3 软化段强度退化
软化段强度退化表征峰值荷载后下降段强度的退化,且下降段刚度并不退化为常数,因此,只需定义峰值荷载的退化(如图8(b)所示),按下式计算:
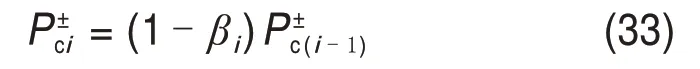
式中:为第i次循环加载后发生性能退化的峰值荷载。
3.2.4 再加载刚度退化
目前广泛应用的恢复力模型大多为顶点指向型模型,即水平反复荷载卸载后再加载点指向上一次加载循环的最大位移处,这种顶点指向型模型并不能考虑再加载刚度的退化。本文引入目标位移考虑锈蚀试件再加载刚度加速退化,如图8(c)所示。在某加载方向(正向或负向),目标位移定义为比该加载方向上一次循环最大位移更大的位移点,其计算公式如下:
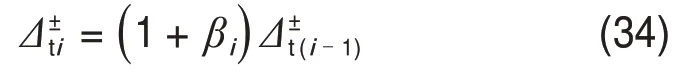
式中:为第i次循环加载时的目标位移。
3.2.5 卸载刚度退化
在弹性阶段,水平反复荷载卸载时没有残余变形,卸载刚度没有退化;当加载位移超过屈服位移后,构件卸载刚度发生退化,如图8(d)所示。卸载刚度退化规则按下式计算:

式中:Kui为第i次循环加载发生性能退化的卸载刚度。
3.3 恢复力模型验证
利用上述建立的恢复力模型对3 榀典型锈蚀RC梁试件滞回曲线进行验证,如图9所示。由图9可见:本文所建锈蚀RC梁恢复力模型在计算滞回曲线时具有较高精度,计算滞回曲线与试验滞回曲线在承载力、变形能力、刚度与强度退化以及滞回特性等方面均符合较好。因此,本文所建恢复力模型可较好地描述锈蚀RC矩形梁在往复荷载作用下的滞回特性,具有较好的适用性。

图8 滞回规则示意图Fig.8 Schematic diagrams of hysteresis rule
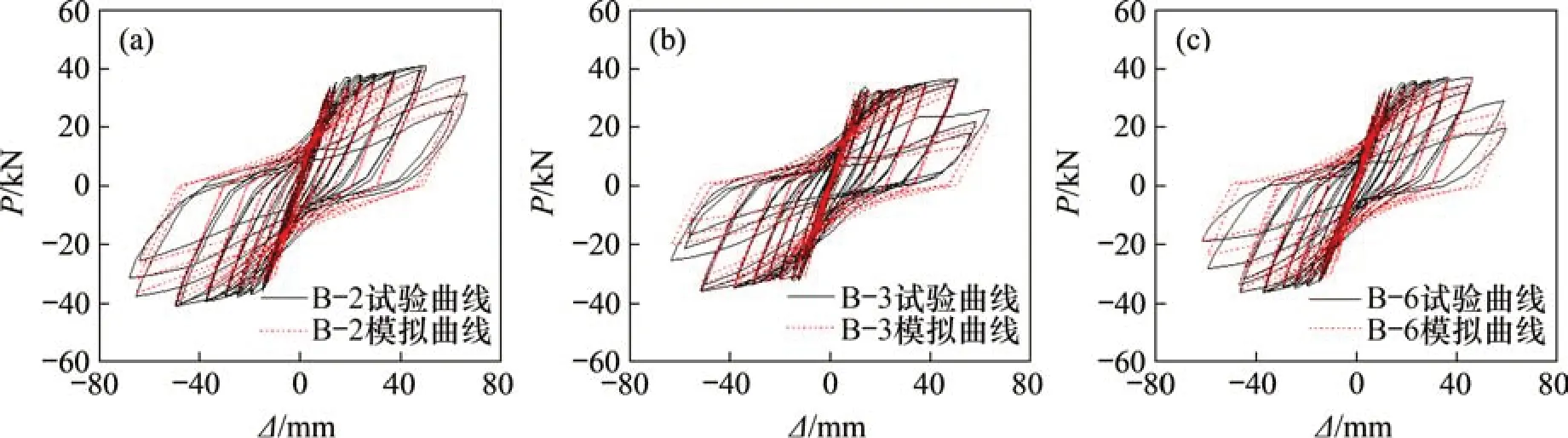
图9 滞回曲线验证Fig.9 Verification of hysteresis curves
4 结论
1)综合考虑锈蚀程度和配箍率对RC矩形梁承载力和变形能力的影响,建立了适用于计算锈蚀劣化RC矩形梁骨架曲线特征点的三折线模型。
2)考虑累积损伤效应造成的强度和刚度退化,引入循环退化指数βi,提出了适用于锈蚀劣化构件的滞回规则,进而建立了考虑锈蚀劣化RC矩形梁的恢复力模型。
3)选取不同锈蚀程度和配箍率的RC矩形梁试件验证该恢复力模型的准确性,计算其骨架曲线特征参数和滞回曲线并与试验值进行对比,吻合度较高,表明所建恢复力模型具有较高的精度和较强适用性。
