盾构隧道开挖引起的邻近群桩竖向位移研究
2020-10-09可文海管凌霄薛齐徐长节耿大新
可文海,管凌霄,薛齐,徐长节,4,耿大新
(1.华东交通大学江西省岩土工程基础设施安全与控制重点实验室,江西南昌,330013;2.江西省地下空间技术开发工程研究中心,江西南昌,330013;3.浙江杭海城际铁路有限公司,浙江嘉兴,314499;4.浙江大学滨海和城市岩土工程研究中心,浙江杭州,310058)
众所周知,盾构隧道在开挖过程中会引起地层损失,当隧道掘进方向存在邻近桩基时,必然会导致邻近桩基产生变形甚至破坏,进而威胁到上部结构安全。因此,准确地预测盾构隧道开挖对邻近群桩的影响,成为城市地铁工程中重点关注的问题之一[1]。
从20世纪70年代开始,众多的国内外学者研究了上述问题[2]。在试验研究方面,MORTON 等[3]利用室内模型试验发现盾构隧道开挖对邻近桩基的影响较大,尤其是在软土中;ONG等[4]采用离心机试验研究了黏性土中的盾构隧道开挖对邻近桩基的影响;在数值模拟方面,CHEN 等[5-6]采用数值方法,将盾构隧道开挖引起的土体位移施加到桩基上模拟桩-土相互作用,进而分析盾构隧道开挖引起的桩基内力与位移;在理论分析方面,两段法是目前研究盾构隧道开挖引起邻近桩基变形的常用方法[7-8],即将盾构隧道开挖引起邻近桩基变形分为2个阶段:第1阶段分析盾构隧道开挖引起的桩基轴线处土体位移;第2阶段将桩基轴线处土体位移直接加到桩基上,再采用合理的模型模拟桩-土相互作用,求解出桩基变形的解析解。两段法的计算步骤清晰简洁,物理意义明确[9-10],能准确计算盾构隧道开挖引起的桩基变形。第1阶段中,LOGANATHAN等[11]提出盾构隧道引起周围土体位移的计算公式,该公式具有良好的计算精度而被广泛应用[12];第2 阶段中,程康等[13]将桩基视为Pasternak 地基上的铁木辛柯梁,研究了盾构隧道开挖引起的桩基水平变形;张治国等[14]考虑了桩侧土体三维效应对桩基的影响,分析了桩基的水平变形及弯矩;李早等[15-16]基于Winkler 地基梁模型并结合有限差分法,研究了盾构隧道开挖引起的邻近桩基竖向位移及内力。
综上所述,众多学者全面分析了盾构隧道开挖引起邻近桩基受力变形的问题,但上述的理论分析中,第2阶段基于弹性地基梁的求解方法需要结合有限差分法[14-16],甚至需要拟合盾构隧道开挖引起的土体位移函数,这些求解步骤大幅增加了计算的复杂程度,无法简便地针对盾构隧道开挖引起的桩基受力变形进行全面地参数分析。
为此,在前人研究的基础上,采用两段法在第2阶段将盾构隧道开挖引起的土体竖向位移转化为荷载施加到桩基上,再基于Winkler地基梁模型结合叠加法原理[17],首先求出集中荷载作用下的桩基位移,其次进行积分得到桩基在分布荷载作用下的桩基位移,最后考虑群桩间的土体遮拦效应[18]求解出盾构隧道开挖引起的邻近群桩竖向位移。此外,将本文计算结果与有限元模拟结果进行对比验证,并深入分析了隧道埋深、地层损失比、桩基直径、土体弹性模量以及群桩间距变化对桩基竖向位移的影响。
1 基本方程的建立与求解
1.1 盾构隧道开挖引起的土体自由场竖向位移
LOGANATHAN等[11]基于线弹性理论提出了盾构隧道开挖引起邻近土体竖向位移的解析解,其计算结果与实测值吻合较好。故本文根据LOGANATHAN 公式,计算盾构隧道开挖引起的邻近土体竖向位移U(x,z)[11]

式中:R为隧道半径;x为距隧道中心线的水平距离;z为距地表的垂直距离;ε0为隧道开挖造成的地层损失比;H为隧道轴线埋深;v为土体泊松比。
1.2 盾构隧道开挖对邻近单桩的影响
图1所示为本文采用的简化计算模型,其中,d为桩基直径,L为桩基的入土深度,x0为桩轴线到隧道中心的距离,此时盾构隧道开挖引起的桩基轴线处(x=x0)处的土体竖向位移为U(z)=U(x0,z)。在盾构隧道开挖引起的桩-土相互作用方面,基于Winkler理论作如下假定:
1)桩为弹性体;
2)土为弹塑性连续变形体;
3)桩-土之间不发生滑移,且始终保持弹性接触。

图1 简化计算模型Fig.1 Simplified calculation model
基于Winkler 模型,桩基竖向位移的控制方程为[19]

式中:W(z)为桩基的位移函数;Ep为桩基弹性模量;Ap为桩基横截面面积;P(z)=kU(z)为桩基受到的竖向外荷载;k为桩侧土的弹簧刚度,根据RANDOLPH等[18]的方法,弹簧刚度k可取:

式中:Gs为土体剪切模量;r0=d/2 为桩基半径;rm为桩的有效影响半径,rm=χL(1-v);χ为经验系数,对于均质土,χ≈2.5[20]。
为求解式(2)中桩基受分布力作用下的位移函数,可先求解受集中力作用的桩基控制方程,图2所示为集中荷载作用下桩基模型图。即令P(z)=0,求其通解,得
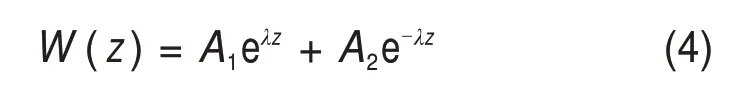
式中:A1和A2为待定系数;
再假设此时桩基底端反力为0,结合式(4),可得桩基轴线任意点ξ受集中力dp(见图2)引起的桩基竖向位移dW*(z)为[21]

图2 集中荷载作用下的桩基模型Fig.2 Pile foundation under concentrated load

在Winkler 地基模型中,任意点ξ因盾构隧道开挖引起的土体位移产生的集中力为

通过Winkler的叠加原理,对式(5)在桩基入土深度范围内积分,可得到不考虑桩基底端反力时盾构隧道开挖引起的桩基竖向位移W*(z)

由于实际的桩基底端反力为Pb=kb[W(L)-U(L)],其中:kb为桩基底端的弹簧刚度;kb=Es为桩基底端土体的弹性模量;hb为桩基底端到基岩的深度;U(L)为桩基底端土体的原位移;W(L)为桩基底端实际竖向位移。根据桩基底部桩-土相互作用的平衡关系[21],可得:
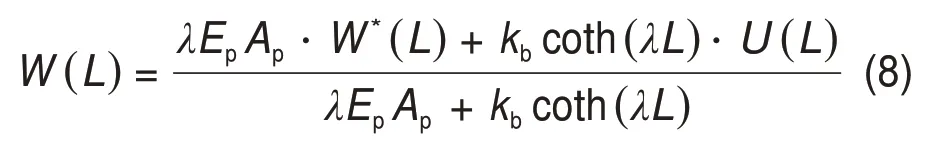
解得桩基底端反力后,将Pb看作桩基在ξ=L处受到的方向向上的集中力,根据Winkler叠加原理便可求得实际的桩基竖向位移
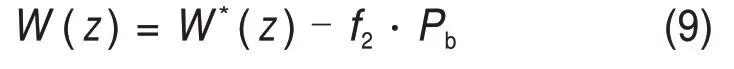
1.3 盾构隧道开挖对邻近群桩的影响
桩基对邻近土体的位移会产生阻碍作用,当盾构隧道开挖引起邻近土体自由场沉降时,桩位处的土体位移会因邻近桩基的阻碍作用而减小,这种现象称为桩基的遮拦效应。因此,土体自由场中的桩基不仅会受到盾构隧道开挖的影响,还会受到邻近桩基的影响。
图3所示为群桩简化计算模型,按照距离隧道轴线的远近将桩基依次定义为桩1、桩2,…,桩i,…,桩n。若土中不存在桩基,盾构隧道开挖引起的桩1 位置处土体竖向位移为U1(z),桩1 因盾构隧道开挖引起的竖向位移为W1(z),则桩1 对土体自由场位移的遮拦效应为ΔW1(z)=U1(z)-W1(z)。根据COOKE 提出的剪切位移法,将桩身周围土体理想地视作同心圆柱体,设桩间距为s,采用RANDOLPH 等[18]提出的桩间土位移传递系数ψ(s),可得到桩2 位置处因桩1 遮拦效应而产生的土体位移U21(z)[19]
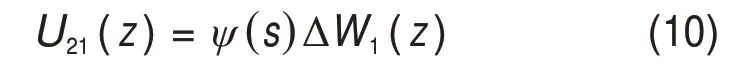

图3 群桩简化计算模型Fig.3 Simplified computing model of group pile
由于桩基遮拦效应引起的位移与土体自由场位移方向相反,因此,在盾构隧道与桩1的共同影响下桩2位置处的土体位移为
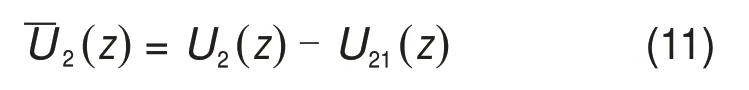
同理可得,桩1位置处因盾构隧道、桩2共同影响而引起的土体位移为(z)=U1(z)-U12(z)。
基于此,本文计算盾构隧道开挖引起邻近群桩竖向位移的具体步骤为:
1)采用式(1)计算出盾构隧道开挖引起各桩基位置处的土体竖向位移Ui(z)(i=1,2,…,n);
2)计算出只考虑单桩时,各桩基在盾构隧道开挖影响下产生的竖向位移Wi(z);
3)根据式(10)和(11)计算出考虑邻近桩基的遮拦效应时,桩i轴线处因盾构隧道与邻近桩基共同影响下的土体竖向位移i,i=1,2,…,n);
2 算例验证
为了验证本文所提方法的准确性,以LOGANATHAN 等[22]应用三维边界元程序GEPAN模拟隧道开挖对邻近2×2群桩影响。该计算假设土体为均质且各向同性的弹性体,土体弹性模量Es为24 MPa,泊松比v为0.5,桩基也为各向同性弹性体,桩基弹性模量Ep为3×104MPa,入土深度L为25 m,直径d为0.8 m,隧道半径R为3 m,隧道轴线埋深H为20 m,地层损失率ε0为1%。第1 排桩距离隧道轴线为4.5 m,第2 排桩距离隧道为6.9 m,两桩轴线间距为2.4 m。
图4所示为本文方法计算结果与GEPAN 程序计算结果的比较。其中图4(a)所示为只考虑单桩时,盾构隧道开挖引起邻近单桩沉降的计算结果。由图4(a)可知:采用本文方法计算的单桩竖向位移曲线与GEPAN 程序计算结果十分吻合,所呈现的规律基本一致,证明了本文方法的准确性。图4(b)所示为考虑群桩的遮拦效应时,盾构隧道开挖引起邻近群桩沉降的计算结果。由图4(b)可知:对于后桩(距隧道轴线更远),采用本文方法计算的桩基竖向位移曲线与GEPAN 程序计算结果基本吻合;但是对于前桩(距隧道轴线更近),本文方法得到的结果整体偏大。这是由于本文方法在分析群桩之间的相互影响时只考虑到邻近桩基对土体自由场的遮拦效应,而实际工程中应该还存在其他效应。当分析前桩对后桩的影响时,前桩引起的土体遮拦效应较大,为群桩之间相互影响的主要影响因素;但分析后桩对前桩的影响时,后桩引起的土体遮拦效应较小,不是主要影响因素。
3 竖向位移影响因素
本文所提计算方法无需拟合土体位移函数,也无需结合有限差分法,计算过程简便,更易于研究桩基竖向位移与各物理参量之间关系。现取如下算例进行分析,隧道的计算参数如下:H为20 m,R为3 m,ɛ0为1%;桩基的计算参数如下:d为1 m,L为25 m,Ep为3×104MPa;取土中存在2根桩,分析盾构隧道对群桩的影响,前桩轴线到隧道的距离x1为5 m,后桩轴线到隧道的距离x2为8 m;土体的计算参数如下:Es为20 MPa,泊松比v为0.3。本文在研究某一参数对桩基竖向位移的影响时,其余参数不变。

图4 隧道附近2×2承台群桩计算结果比较Fig.4 Comparison of results of 2×2 pile group with cap adjacent to tunneling
3.1 隧道埋深
为研究隧道埋深变化对群桩竖向位移的影响,分别分析隧道埋深为10,15和20 m的情况。
图5所示为不同影响因素变化下的桩基竖向位移。由图5(a)可见:隧道埋深从10 m 增加到20 m时,两桩的竖向位移均增大,但增幅在减小。这是由于盾构隧道开挖后,隧道中心线上方的土体向下位移,中心线下方的土体向上位移,因此,隧道埋深增加将引起了土体向下位移的范围增大,此时,土中桩基便受到更多的土体向下位移的荷载,导致其产生了更大的竖向位移。
3.2 地层损失比
为研究地层损失比变化对群桩竖向位移的影响,取地层损失比分别为0.5%,1.0%和2.0%进行分析。从图5(b)可见:桩基的竖向位移随着地层损失比增加而等比例增加。这是因为式(1)中,地层损失比与隧道开挖引起的土体位移为正比例关系,当地层损失比增大时,隧道开挖引起的土体位移将随之等比例增加,进而导致邻近群桩受盾构隧道开挖影响的程度等比例增大。
3.3 桩基直径
分别取桩基直径为0.50,0.75和1.00 m分析桩基直径变化对群桩竖向位移的影响。从图5(c)可见:桩基直径从0.50 m 增加到1.00 m 时,两桩的竖向位移均有略微减小。这是由于桩基直径增加会导致其刚度增大,进而引起其抵抗桩周土体位移影响的能力增加。因此,在同样的土体位移荷载作用下,桩基直径增加可引起其产生的竖向位移减小。
3.4 土体弹性模量
分别取土体的弹性模量分别为10,20 和30 MPa,研究土体弹性模量变化对群桩竖向位移的影响。从图5(d)可见:随着土体弹性模量增加,两根桩基的顶端竖向位移(最大位移)均增大,但底端竖向位移均减小。结合3.1节分析认为,土体弹性模量增加引起隧道中心线上方的桩体受到土体向下位移的荷载增大,隧道中心线下方的桩体受到土体向上位移的荷载增大,同时桩基底端受到土体的反力也随之增大,这导致了桩顶位移增大而桩底位移减小的现象。
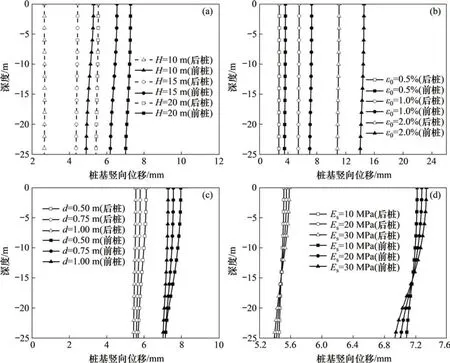
图5 不同影响因素变化下的桩基竖向位移Fig.5 Vertical displacement of pile foundation under different influencing factors
3.5 桩基间距
为研究桩基间距变化对群桩竖向位移的影响,取表1所列工况进行分析。

表1 不同桩基间距工况Table 1 Working conditions of different pile foundation spacing m
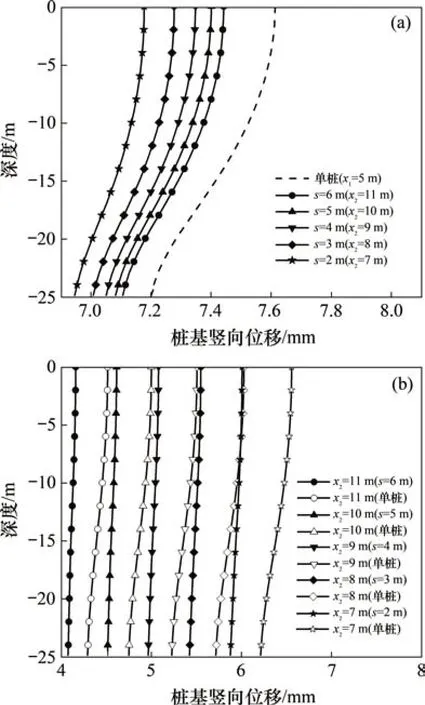
图6 桩基间距离变化对桩基竖向位移的影响Fig.6 Influence of different pile spacing on vertical displacement
图6所示为不同桩基间距下的桩基竖向位移。从图6(a)可见:随着后桩的逐渐远离,前桩的竖向位移增大,且逐渐接近单桩的竖向位移。这是由于后桩与前桩的距离增加时,其对前桩造成的遮拦效应减弱。从图6(b)可见:随着后桩到隧道的距离越来越远,后桩的竖向位移逐渐减少,且与单桩时竖向位移的差值越来越小。这是因为后桩在远离隧道时,其受到盾构隧道开挖的影响减小,同时其与前桩的间距在增加,因此,受到前桩遮拦效应的影响也逐渐减弱。由此可见:桩间距增加可导致群桩间的遮拦效应减弱,桩基的相对竖向位移增加;桩基与隧道距离增加可导致桩基受到盾构隧道开挖的影响减小、桩基的竖向位移减小。
4 结论
1)采用本文方法计算盾构隧道引起的邻近单桩竖向位移与有限元结果吻合,但在考虑群桩的遮拦效应时,计算的前桩竖向位移与有限元结果相比整体偏大。
2)控制其余参数不变时,隧道埋深增加及隧道开挖引起的地层损失比增大均会导致邻近群桩的竖向位移增大。
3)当桩基直径增大时,邻近群桩因盾构隧道开挖引起的竖向位移均略微减小。
4)土体弹性模量增加会导致邻近群桩的顶端竖向位移(最大位移)增大,底端竖向位移减小。
5)桩基与隧道距离增加可减弱盾构隧道开挖对邻近桩基的影响,减小桩基竖向位移;群桩间距增大导致桩基间的遮拦效应减弱、桩基的相应竖向位移增大。
