锈蚀钢框架梁抗震性能试验及地震损伤模型
2020-10-09尚志刚郑山锁张晓辉郑淏董晋琦贺金川
尚志刚,郑山锁,张晓辉,郑淏,董晋琦,贺金川
(1.西安建筑科技大学土木工程学院,陕西西安,710055;2.西安建筑科技大学结构工程与抗震教育部重点实验室,陕西西安,710055;3.西安建筑科技大学建筑设计研究院,陕西西安,710055)
我国是临海国家,大量在役钢结构长期处于近海大气环境中,而钢结构的锈蚀速率相较于一般大气环境更快[1]。锈蚀后的钢结构由于钢材强度降低、构件有效截面削弱和应力集中等问题,其力学性能与抗震性能会发生不同程度退化[2-4]。当长期受到锈蚀的钢结构遭遇突发地震时,会发生严重破坏,并造成巨大的生命财产损失,因此,有必要研究近海大气环境下锈蚀钢框架梁的抗震性能。结构损伤无疑对其在后续服役龄期中的抗力和剩余寿命产生重大影响,因此,提出可以合理反映结构或构件地震损伤演化规律的计算模型,是一个亟待解决的重大问题。迄今为止,国内外学者提出了诸多有影响力的地震损伤模型[5-11],如DARWIN等[5]认为每一个结构或构件具有一定的塑性变形能,将损伤指数定义为每一圈滞回能的累积量与总能量的比值,然而,该模型不能考虑加载制度对损伤的影响;董宝等[6]全面考虑了影响破坏模式的因素,提出了强调最大塑性变形作用的位移型损伤模型,然而,该模型未考虑滞回能累积效应;PARK 等[7]基于大量钢筋混凝土梁柱构件试验结果,提出了可同时反映变形和能量综合损伤的双参数模型,然而,该模型采用的线性组合模式导致在单调加载情况下,构件破坏时的损伤指数不等于1。鉴于此,本文对近海大气环境下的锈蚀钢框架梁试件进行拟静力加载试验,研究不同锈蚀程度对钢框架梁抗震性能的影响。在此基础上,分析可反映锈蚀钢框架梁地震损伤演化规律的指标,并综合考虑加载制度、组合模式等对损伤的影响,提出能够较好地模拟锈蚀钢框架梁地震损伤演化过程的变形-滞回耗能损伤模型。研究成果可为近海大气环境下锈蚀钢框架梁的抗震性能及地震损伤评估提供理论依据。
1 试验方法和过程
1.1 试件设计
本文设计并制作了5榀钢框架梁试件,以锈蚀程度作为变化参数。试件选用热轧H 型钢,截面规格(截面高度×截面宽度×腹板宽度×翼缘宽度)为300.00 mm×150.00 mm×6.50 mm×9.00 mm,材质为Q235B。试件腐蚀程度根据锈蚀时间的不同,分为5 个级别,即试件GL-1,GL-2,GL-3,GL-4 和GL-5 分别对应未锈蚀、锈蚀480 h、锈蚀960 h、锈蚀1 920 h 以及锈蚀2 880 h。试件几何与截面尺寸如图1所示。
1.2 试件加速腐蚀试验
由文献[13]可知,人工气候模拟环境能够达到与自然环境相同的锈蚀作用过程。因此,本文通过设定人工气候实验室参数模拟近海大气环境[14],以实现试件的加速锈蚀。具体参数设置如下:实验室温度为33~37 ℃;实验室湿度为95%以上;腐蚀溶液质量浓度为45~55 g/L;腐蚀溶液pH 为6.5~7.2;腐蚀循环模拟制度为喷5 min,停5 min;沉降量为l~2 mL/(80 cm2·h)。
1.3 拟静力加载装置和加载制度

图1 钢框架梁试件详细尺寸Fig.1 Detailed size of steel frame beams

图2 试验加载装置Fig.2 Test loading device
本试验采用悬臂梁式拟静力加载方法对钢框架梁试件进行低周往复循环加载,加载装置如图2所示。为实现支座固定的边界条件,用压梁将支座梁固定在刚性地面上,底梁两端由千斤顶与顶梁固定,以避免发生滑移事故;梁端通过1 台30 t的MTS 电液伺服作动器施加水平往复荷载;为防止加载过程中出现平面外失稳,另在梁的两测设置侧向支撑。
为了准确地模拟地震激励下试件的破坏过程,保证试验结果的可靠性与合理性,根据文献[15],本实验采取的加载制度为位移控制的变幅加载制度,如图3所示。其中前3个位移级每级循环加载6 次,第4 个位移级往复循环加载4 次,之后每个位移级循环加载2次,直至试件发生破坏,停止加载。正式加载前,应先将试件进行预加载,以检验并校准加载装置及量测仪表[16]。整个试验过程由MTS 电液伺服结构试验系统与计算机联机实施程控加载,同时在试件主要控制截面上布置电阻应变片以收集整个受力过程中的应变。
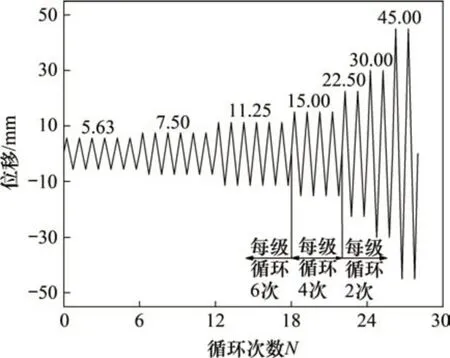
图3 试验加载制度Fig.3 Loading procedures of tests
1.4 钢材失重率及力学性能
本文采用钢材失重率Dw表征试件锈蚀程度。依据文献[17],选取钢框架梁试件所用的同批次钢材并切取板厚分别为6.50 mm和9.00 mm的标准试件。每种厚度的试件以2个为1组,制作10组共计20 个试件。对各标准试件进行加速锈蚀,并用稀盐酸除去试件表面锈层后烘干称质量,测得钢材质量损失率。
本文用试件在锈蚀过程中的质量损失来描述钢材质量损失率Dw,其表达式为

式中:W0为锈蚀前的钢材质量;W1为经过锈蚀的钢材在除锈后的质量。
测得钢材质量损失率后,依照文献[18],将除锈后的标准试件进行单向拉伸试验,获得锈蚀钢材力学性能,表1所示为钢材平均质量损失率及力学性能。
2 试验结果
2.1 试验现象及破坏模式
5个试件在水平低周往复荷载作用下的破坏历程基本相似。加载初期,试件处于弹性阶段;随着水平加载位移增大,试件进入弹塑性阶段;当加载位移级达到45.00 mm左右时,试件GL-5达到最大承载力;当加载位移级达到60.00 mm左右时,试件GL-1,GL-2,GL-3和GL-4达到最大承载力;当加载位移级达到75.00 mm左右时,试件GL-4和GL-5水平承载力达到峰值荷载的85%,发生破坏;当加载位移级达到82.50 mm 左右时,试件GL-1,GL-2和GL-3水平承载力达到峰值荷载的85%,发生破坏。
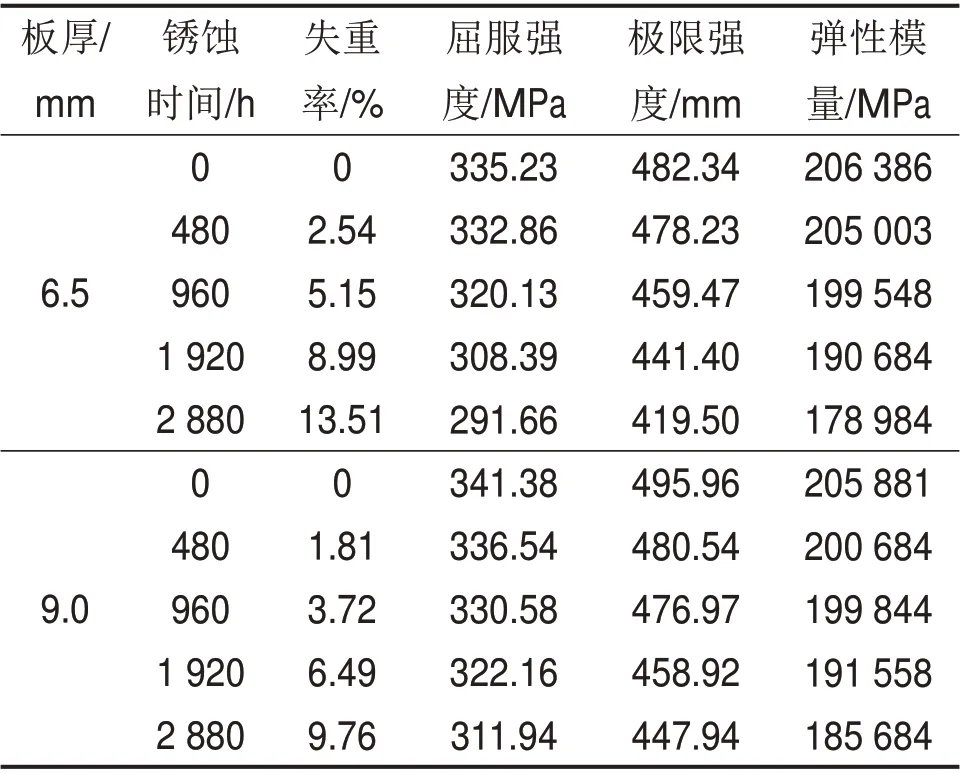
表1 钢材平均失重率及力学性能Table 1 Average weight-loss rate and mechanical properties of steels
在弹性阶段,试件的荷载与位移均呈线性增长,梁底部区域的翼缘和腹板尚无显著局部变形。在弹塑性阶段,试件梁底部区域的翼缘和腹板发生明显变形,形成塑性铰,水平承载力开始下降。随后,梁腹板根部出现裂缝,并向翼缘快速发展,直至受拉侧翼缘根部裂缝贯通,试件发生延性破坏。各试件破坏形态如图4所示。
对比锈蚀程度不同的试件,其破坏过程与特征呈现出一定差异:随锈蚀程度增加,试件水平承载力下降,峰值位移减小,板件局部屈曲程度加重。
2.2 滞回曲线
荷载-位移滞回曲线是加载位移与水平荷载的关系,可以较直观地展现试件的承载力水平和耗能能力。将本次试验试件在加载过程中采集的荷载、位移数据绘制成P-Δ滞回曲线,如图5所示。由图5可见:总体而言,各个试件的滞回曲线均呈较饱满的梭形,无明显捏缩现象,说明锈蚀钢框架梁仍具有较强的抗震能力和耗能能力。
在整个加载过程中,屈服前,各试件滞回曲线接近重合于1条直线,卸载后没有残余变形,此时试件累积损伤基本为0,可以忽略。随着加载,各试件滞回曲线的加载半环和卸载半环从直线中逐渐分离并呈梭形,形态愈发饱满,面积逐渐变大、无明显“捏拢”现象,滞回耗能亦随之增强;当荷载卸为零时,试件出现残余变形,加载和卸载曲线的斜率随加载位移增加逐渐减小,表明往复荷载作用下试件的刚度发生退化。此外,在同一加载位移级下,不同加载循环的滞回曲线相差不大,表明试件承载能力和刚度随着循环次数增加退化不明显。当水平承载力达到峰值荷载后,随着水平加载位移进一步增加,试件承载力显著降低,加载和卸载刚度退化速率加快,残余变形继续增大,滞回环面积持续增加,试件耗能能力随之增大。
锈蚀程度对试件抗震性能的影响较为显著,锈蚀更严重的试件,其承载力和刚度相对较低,滞回环面积相对较小,强度衰减和刚度退化现象相对较严重,表明钢框架梁的承载能力、变形能力与耗能能力均随锈蚀程度增加而逐渐减小。

图4 试件破坏形态Fig.4 Failure patterns of specimens
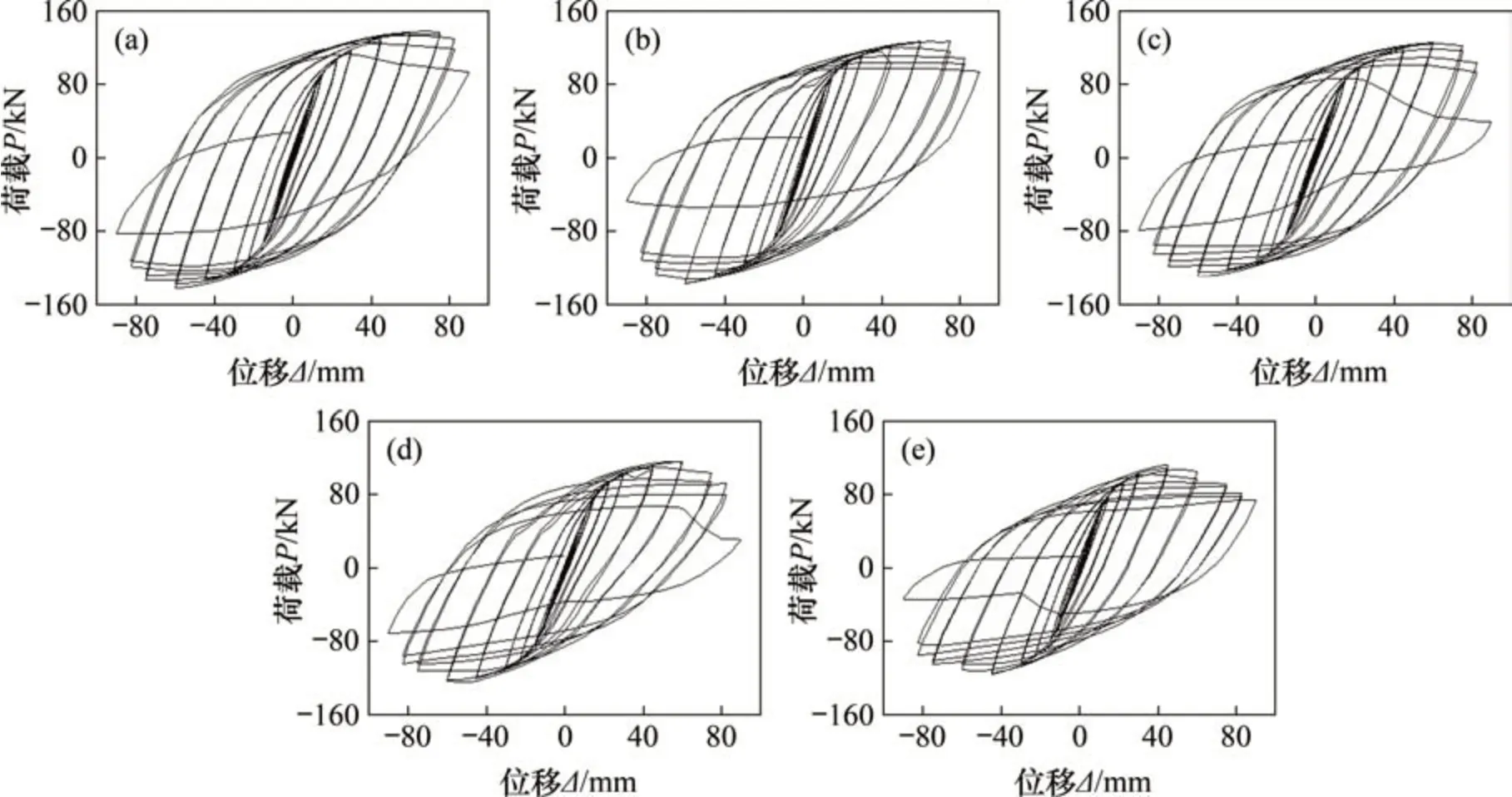
图5 试件滞回曲线Fig.5 Hysteretic curves of specimens
2.3 骨架曲线
将各试件P-Δ滞回曲线每循环的峰值点相连即可得到试件的骨架曲线。试件的变形、承载力和刚度等的变化过程可在骨架曲线上以较直观的形式反映。各试件骨架曲线如图6所示。
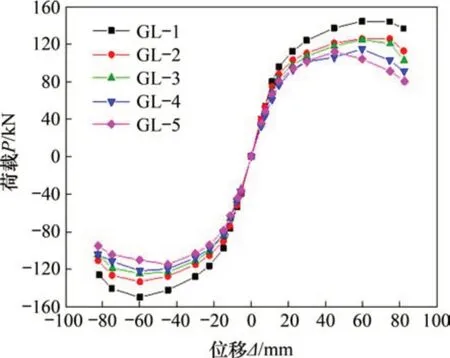
图6 试件骨架曲线Fig.6 Skeleton curves of specimens
进一步分析图6得到各试件的特征点以及延性系数等性能指标,如表2所示。其中应变片测得的截面边缘屈服所对应点为屈服点,骨架曲线峰值荷载的85%所对应的点为极限点。由图6和表2可知:
1)试件在弹性工作阶段时,骨架曲线大体呈线性增长趋势;进入弹塑性工作阶段后,骨架曲线开始弯曲,斜率减小,试件刚度逐步下降。
2)加载至峰值位移后,试件进入破坏阶段,骨架曲线开始下降,试件承载力持续降低,刚度出现负值。
3)随着锈蚀程度增加,试件屈服点、峰值点和极限点的位移和荷载以及延性系数均呈降低趋势,骨架曲线下降段亦逐渐变陡,表明试件的承载力及延性随着锈蚀程度增加而减小。
2.4 强度衰减与刚度退化
本文定义试件滞回曲线每1次循环的峰值荷载为强度指标,每1次循环原点和峰值荷载点连线的斜率为刚度指标。各试件的强度与刚度退化曲线如图7所示。
由图7(a)可知:峰值荷载前,在同一位移级下,随着循环次数增加,试件的强度基本无明显变化,且锈蚀对试件强度的影响也不明显;峰值荷载后,在同一位移级下,随着循环次数增加,试件的强度显著降低,且随着锈蚀程度增加,试件强度衰减逐渐加快。
由图7(b)可知:随着加载位移增大,试件刚度逐渐降低;随着锈蚀程度增加,在相同水平位移下,试件刚度包括初始刚度均发生一定程度减小,且刚度退化速率逐步加快。
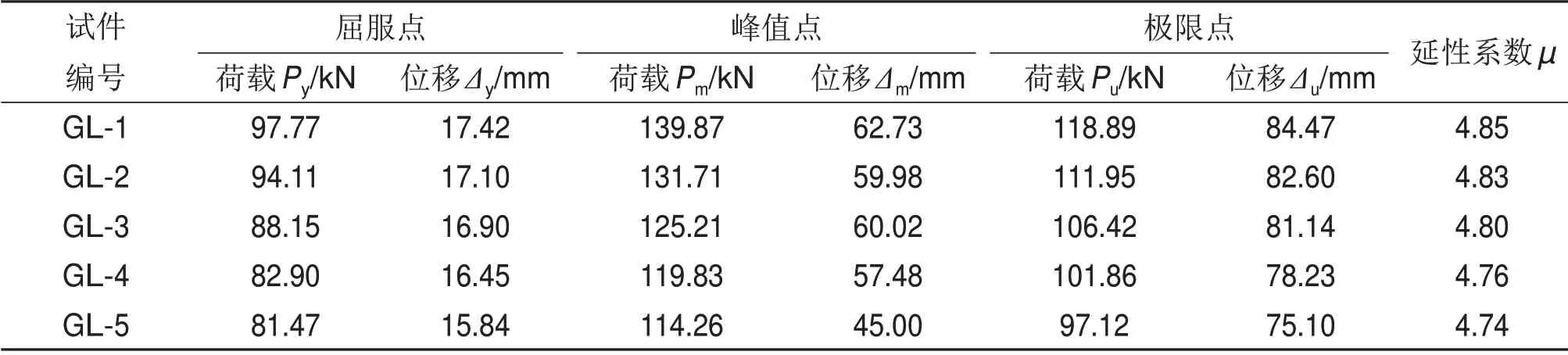
表2 试件特征点及延性系数Table 2 Characteristic points and ductility coefficients of specimens
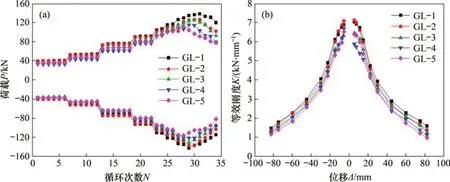
图7 试件强度和刚度退化曲线Fig.7 Strength and stiffness degradation curves of specimens
2.5 耗能能力
耗能能力可作为评定构件或结构抗震性能的重要指标,一般可用累积耗能来表示。各试件累积耗能曲线如图8所示。由图8可知:随着循环次数增加,各试件的累积耗能逐渐增大;随着锈蚀程度增加,各试件累积耗能逐渐降低。
3 锈蚀钢框架梁地震损伤模型
3.1 双参数模型的选取
锈蚀钢框架梁在地震作用下的损伤不断累积,其力学性能(强度P和刚度K等)亦随着损伤发展而不断退化,因此,可以通过强度衰减与刚度退化反映锈蚀钢框架梁在地震作用下的损伤程度及发展趋势。
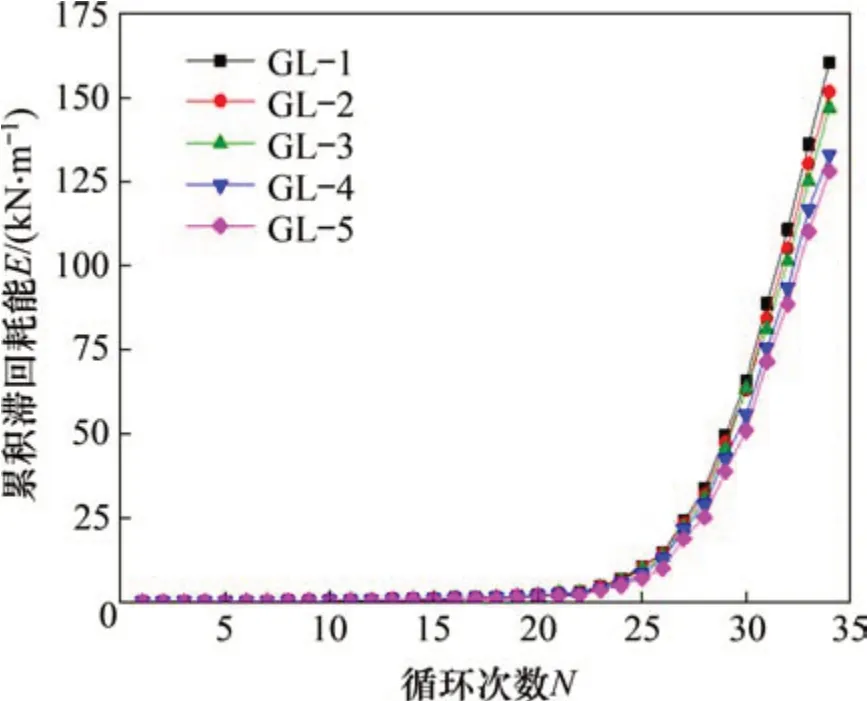
图8 试件累积耗能曲线Fig.8 Cumulative energy dissipation curves of specimens
在等幅位移加载和变幅位移加载2种加载制度下,锈蚀钢框架梁强度衰减与刚度退化如图9所示。由图9可见:无论对于等幅加载还是变幅加载,强度衰减和刚度退化都会造成滞回曲线变化,因此,滞回耗能E可以描述锈蚀钢框架梁的损伤。对于更贴近地震作用的变幅加载(图9(c)和9(d)),变形Δ同样能描述锈蚀钢框架梁的强度衰减与刚度退化。
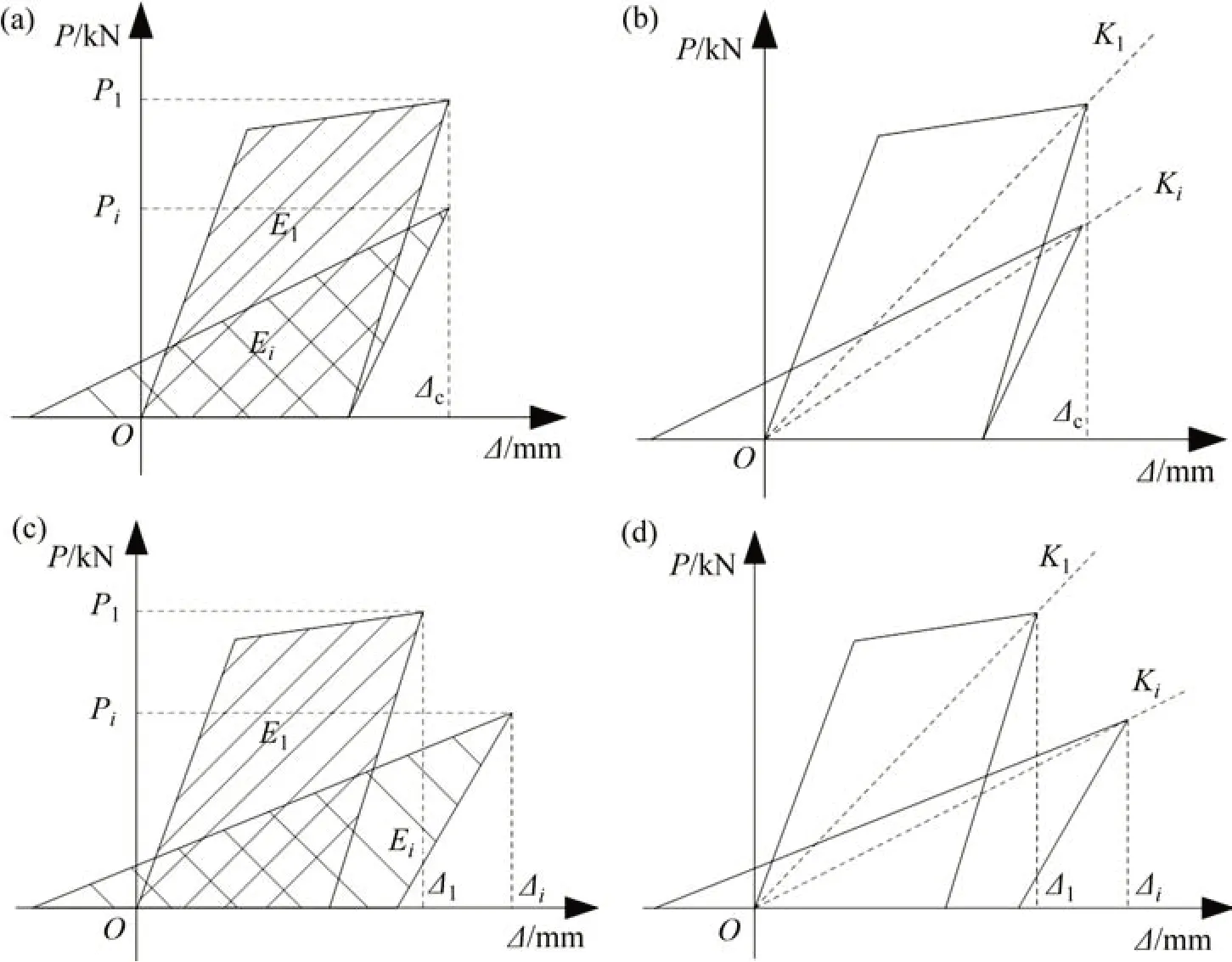
图9 锈蚀钢框架梁强度衰减与刚度退化Fig.9 Strength attenuation and stiffness degradation of corroded steel frame beams
综上所述,变形与滞回耗能皆能明显反映钢框架梁的地震损伤演化,因此,相对于单参数损伤模型,基于变形-滞回耗能的双参数损伤模型更能全面合理地评估钢框架梁的地震损伤。
此外,根据文献[9],加载制度是影响结构或构件损伤的主要因素之一,因此,本文建立的地震损伤模型考虑了加载制度对损伤的影响。
3.2 建立地震损伤模型
基于上述分析,本文将通过引入组合系数α,将变形和滞回耗能这2 项损伤分量进行非线性组合,反映锈蚀钢框架梁在地震作用下的发生的损伤。损伤模型表达式中变形分量与滞回耗能分量分别用Dδ与DE表示,则地震作用下钢框架梁的变形-滞回耗能双参数损伤模型表达式为

2项分量Dδ与DE的具体表达式分别是
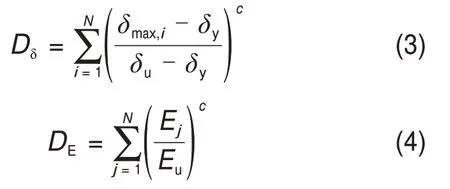
综上,本文建立的地震损伤模型表达式为
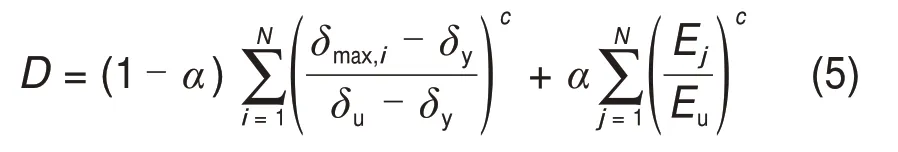
其中,
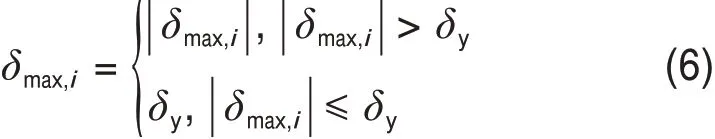
式中:D为损伤指数;δmax,i为第i次半循环时构件达到过的最大变形;δy和δu分别为构件在单调荷载作用下的屈服变形和极限变形;N为构件加载的最大半循环次数;Ej为构件在第j个加载半循环时的滞回耗能;Eu为构件单调荷载至破坏时的极限耗能;c为试验参数。
本文提出的地震损伤模型全面考虑了变形和滞回耗能对构件损伤的影响,具体表现在以下3个方面:
1)根据已有研究成果,采用相对更合理的变形-滞回耗能非线性组合模式,使其在单调加载情况下,构件破坏时的损伤指数D等于1;
2)考虑了加载制度的影响,可更符合实际情况下结构的地震响应;
3)关于弹性阶段的变形损伤分量的规定,损伤指数D可在下界收敛于0,更符合损伤指数性质[12]。
3.3 半循环最大位移
构件在弹性阶段时,每半循环的最大位移δmax,i应等于δy,即忽略变形分量所引起的损伤,仅考虑滞回耗能分量对损伤的影响;构件达到屈服状态后,当构件在第i+1 次半循环中达到的最大位移δmax,i+1不大于构件在前i次半循环中达到的最大位移δ'max,i时,忽略第i+1次半循环中位移分量对构件损伤产生的影响,仅考虑其滞回耗能分量的损伤;反之,构件第i+1次半循环损伤则由变形分量与滞回耗能分量组合而成。
对于本文的加载制度,以屈服后加载位移级为45.00 mm 为例,该位移级往复循环加载2 次,半循环次数共4 次,但是在计算损伤指数时,第1次半循环的损伤由变形分量与滞回耗能分量组合而成,第2~4次半循环由于达到的最大位移等于第1 次半循环达到的最大位移(45.00 mm)。因此,仅考虑滞回耗能分量的损伤,忽略位移分量对构件损伤产生的影响。屈服后的其他加载位移级损伤计算与此相同。
由于对上述半循环最大位移的考虑,因此,本文地震损伤模型能较好地体现加载制度这一因素,在理论上更合理。
3.4 构件的变形与耗能的确定
图10所示为构件变形与耗能参数示意图。
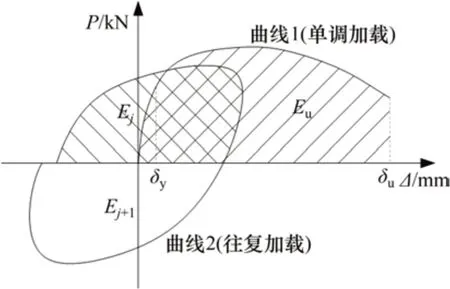
图10 构件变形与耗能参数示意图Fig.10 Schematic diagram of deformation and energy dissipation parameters
Ej由低周往复循环加载试验计算得到,而试验采集δy,δu和Eu代价较大,因此,本文采用ABAQUS 有限元软件建模[19],如图11所示。对试件进行单调加载模拟,从而得到各试件在单调荷载作用下的的屈服变形、极限变形和极限耗能。
图11 ABAQUS有限元模型Fig.11 FEM built by ABAQUS
改变钢材本构模型参数,考虑锈蚀对钢材屈服强度、极限强度和弹性模量等力学性能的影响,此时,试件的有限元模型截面尺寸保持不变[20]。不同锈蚀程度的钢材力学性能见表1。
3.5 组合系数α和试验参数c
计算试验参数c需先确定各试件破坏时对应的位移级与半循环次数。因此,根据表2中各试件的极限点试验数据,结合本文采取的加载制度,试件GL-1 在加载位移级为82.50 mm 的第2 圈负循环时发生破坏,GL-2 和GL-3 皆在加载位移级为82.50 mm 的第1 圈正循环时发生破坏,GL-4 在加载位移级为75.00 mm的第2圈负循环时发生破坏,GL-5 在加载位移级为75.00 mm 的第1 圈正循环时发生破坏。
KUMAR 等[9,21]指出,组合系数α一般取0.10~0.20,并且组合系数α和试验参数c不能同时确定,优先确定α的计算成本更低。c离散性可以作为评价α取值合理性的指标,使c离散性越小的α更加合理。因此,本文结合试验结果以及式(5),试算α分别取0.10,0.15 和0.20 时各试件c并对比其离散性(表3),最终取组合系数α为0.20。
在确定组合系数α后,可以分析求解试验参数c。根据本次试验,试验参数c主要考虑锈蚀程度(质量损失率)的影响。根据试件破坏时,损伤指数D取1[12],可反推计算出各试件试验参数c取值。试验参数c随失重率Dw变化的曲线如图12所示。
由图12可知:将GL-1、GL-2 和GL-3 试件归为Ⅰ类试件,将GL-4和GL-5试件归为Ⅱ类试件,则对于Ⅰ类和Ⅱ类试件,其试验常数c随质量损失率Dw皆呈增大趋势;对比Ⅰ类试件和Ⅱ类试件可知,Ⅱ类试件的试验常数c骤降,这是由于当锈蚀增大到某一程度时,试件破坏时的加载位移级会减小,即Ⅰ类试件是在加载位移级82.50 mm 时破坏,而Ⅱ类试件是在加载位移级75.00 mm 时破坏,这与试验结果相符。

表3 GL-1至GL-5试件试验参数离散性Table 3 Test parameters discreteness of GL-1 to GL-5 specimens
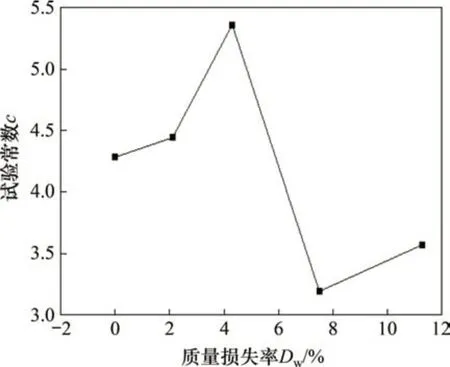
图12 试验常数与质量损失率关系曲线Fig.12 Relationship curve between test constant and mass loss rate
4 模型有效性验证
为了验证本文所建损伤模型的有效性,分别采用本文模型和欧进萍等提出的模型[8,22]计算损伤指数,计算结果及对比如图13所示。由图13可见:本文损伤模型计算的损伤指数在弹性阶段时皆收敛于0,表明此时产生的损伤很小;进入弹塑性阶段后,损伤开始迅速发展,并形成具有一定斜率的位移级“平台”。随着循环次数增加和加载位移级增大,损伤指数与位移级“平台”的斜率越来越大,且位移级“平台”;间的损伤指数差值亦越来越大,表明损伤逐渐增大且发展速率越来越快。欧进萍等[8]提出的损伤模型所计算的初始损伤也较小,但仍不收敛于0,且其计算结果高估了钢框架梁的损伤程度。

图13 本文模型与欧进萍模型计算结果对比Fig.13 Comparison of computation results of the proposed model and Ou Jinping model
此外,锈蚀对损伤的发展也有一定影响。对于同一模型的计算结果,GL-1,GL-3以及GL-5试件的损伤曲线总体趋势是一致,但2种损伤模型的计算结果都表明,随着锈蚀程度增大,试件的损伤发展更快,具体表现为同一循坏次数下,试件GL-5,GL-3 和GL-1 的损伤指数依次减小;此外,当锈蚀达到某一程度时,会极大地增加试件的损伤发展速度,对于本文模型来说,GL-5 试件的损伤指数在加载位移级为75.00 mm时便达到1,发生了破坏,而GL-1和GL-3试件的损伤指数在加载位移级为82.50 mm时才达到1。
综上所述,本文所建损伤模型能够较好地模拟近海大气环境下锈蚀钢框架梁的地震损伤演化过程。
5 结论
1)不同锈蚀程度钢框架梁试件的破坏模式基本相同,分为弹性、弹塑性和塑性破坏3 个阶段,破坏形态均为受拉侧翼缘根部裂缝贯通导致的延性破坏,且随着锈蚀程度增加,试件局部屈曲程度加重。
2)锈蚀对钢框架梁抗震性能有极大影响。随着锈蚀程度增加,钢框架梁的承载能力、变形能力与耗能能力逐渐降低,强度衰减和刚度退化明显。
3)根据试验结果与理论分析,提出了适用于锈蚀钢框架梁的变形-滞回耗能损伤模型,并给出了模型参数的具体定义与确定方法。
4)本文模型计算结果符合损伤指数性质,能够较好地模拟锈蚀钢框架梁的损伤演化过程,研究成果可为锈蚀钢框架梁的地震损伤评估提供理论依据。
