多个列车轮载作用下铁路道床结构安定性分析
2020-10-09王康宇庄妍张占荣张升
王康宇,庄妍,张占荣,张升
(1.浙江工业大学土木工程学院,浙江杭州,310014;2.东南大学土木工程学院混凝土及预应力混凝土结构教育部重点实验室,江苏南京,211189;3.长沙理工大学公路养护技术国家工程实验室,湖南长沙,410114;4.中铁第四勘察设计院集团有限公司,湖北武汉,430063;5.中南大学土木工程学院高速铁路建造技术国家工程实验室,湖南长沙,410075)
随着工业技术和工程建设的快速发展,现代的结构设计理念需要在保证结构安全的前提下,尽可能考虑经济效益,这就对工程设计和既有工程结构的承载性能评估提出新挑战。铁路和道路结构的路面、路基及其以下一定范围内的地基在交通荷载的长期循环作用下将会产生振动,且随着交通荷载作用次数增加而出现较大的塑性变形累积现象,其破坏形式往往是由于塑性变形逐渐累积而非突然的崩塌破坏[1]。因此,现有的基于弹性理论和经验方法的设计与分析理念不能反映其破坏的本质。安定分析能够有效确定交通荷载作用下结构的长期响应,反映结构破坏的本质及实际的安全程度,因而在交通荷载作用下的结构中得到了广泛应用。SHARP等[2]将路面结构的破坏形式与安定理论建立了联系,基于MELAN定理提出了二次曲线法(也称圆锥曲线法)求解平面情况下单层路面和双层路面的安定荷载,并总结了各结构层的材料参数对安定荷载的影响规律;YU 等[3]提出了基于Hertz接触荷载的二维和三维路面结构静力安定荷载的解析方法,但该方法放松了对残余应力场满足屈服条件的限制[4-5];孙阳等[6]基于静力安定定理研究了平面应变条件下2层路面结构的安定性,分析了路面材料参数和各结构层厚度等因素对安定荷载的影响规律;王娟等[7]总结了安定理论在道路结构中的应用情况,提出了基于安定下限定理的道路路面结构设计方法。最近,在经典静力安定理论的基础上,QIAN 等[8-10]基于有限元模型研究了移动荷载作用下结构中的动应力分布,通过构建稳态动应力条件下结构中的残余应力场,提出了动力安定性下限值的预测方法,揭示了交通荷载形式和移动速度等对结构安定性的影响规律。目前,安定理论在铁路工程中的应用多集中于轮轨接触应力和轮轨磨损等问题,如LANGUEH等[11]考虑车轮材料的循环硬化效应,基于弹性安定和塑性安定概念,提出了基于稳态算法的数值方法,预测实际情况下车轮滚动接触疲劳裂纹的萌生;PANUNZIO 等[12]基于弹性安定理论,假设列车轮轨服从Dang Van 准则,研究了轨道几何不平顺对轮轨动力相互作用和钢轨疲劳磨损的影响;HASAN[13]基于von-Mises 屈服准则和Hertz 接触理论,从轮载和钢轨的抗拉强度出发,确定了理想的最小接触面积,优化了轮轨型线;CHEN等[14]在计算轮轨非赫兹接触特性和轮轨轮廓演化的基础上,基于安定理论评估了道岔累积表面启动滚动接触疲劳(RCF)。同时,现有研究仅考虑了单个列车轮载作用,忽略了多轮载通过轨道结构传递的应力叠加作用,不能准确计算铁路道床结构的应力分布规律[15-16]。为了更全面地了解铁路道床的安定行为,本文基于列车轮载的传递机理,采用Gauss 函数计算轨枕荷载分担比,结合Melan静力型安定定理,研究多轮载作用下单层道床结构的安定荷载及其影响因素,以期为铁路道床结构的优化设计提供借鉴和参考。
1 列车轮载的简化
1.1 单个列车轮载作用的轨枕荷载分担比
列车荷载作用于轨道结构上,经过钢轨、轨枕和道床,最终传递到路基结构中。从道床-路基结构承载能力和沉降控制的角度来讲,明确列车荷载的分布规律和轨枕荷载分担比对道床-路基结构中的动应力研究和结构的优化设计具有重要的意义。文献[17]指出:单轴轮载作用在钢轨上一般由5 根轨枕承担,各轨枕分担轮载的比分别为10%,20%,40%,20%和10%,如图1所示,由于需要将列车的动力问题考虑在内,图1中所示的列车轮载应动轮载,可由下式计算:
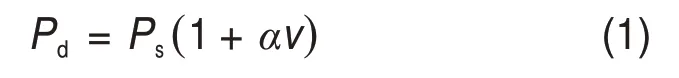
式中:Pd为单个动轮载,kN;Ps为单个静轮载,kN;α为动力冲击系数或速度影响系数;v为列车行驶速度,km/h,若v为300~350 km/h,则α=0.003,若v为200~250 km/h,则α=0.004;重载货车的行驶速度一般为120 km/h,其α可取0.004。

图1 列车轮载在5根轨枕上分担的示意图Fig.1 Distribution of wheel load on five sleepers
尽管文献[17]给出的方法具有使用方便、易于记忆的优点,且有一定的安全容许度,但应用时通常假设轮载恰好作用于轨枕正上方,而当列车轮载位于其他位置处时,各轨枕所承担的轮载分担比的确定较复杂。吕文强等[18]基于Winkler 弹性连续支撑梁模型,假定轨道结构为线弹性连续均匀分布,指出轨枕分担轮载的比值与Gauss函数曲线形态相似,提出了如式(2)所示的Gauss函数表达的各轨枕分担轮载比αi近似计算方法:

式中:σ为形状参数;i为承担列车轮载的轨枕编号;xi为编号为i的轨枕中点坐标;n为承担列车轮载的轨枕数量,若列车轮载位于轨枕正上方,则n=5,若列车轮载位于两相邻轨枕中间的某一位置处,则n=6。
以列车轮载作用于轨枕正上方为例,采用Gauss 函数法计算轨枕荷载分担比。假设60 kg/m的标准钢轨由III 型钢筋混凝土轨枕支承,其间距为0.65 m,1 km 铺设1 539 根轨枕,此时n=5,则各轨枕的荷载分担比计算结果如图2所示。假定轨道结构为线弹性连续均匀分布,则随着列车轮载移动,尽管列车轮载的位置发生了改变,但轨枕荷载分担比的曲线形状仍保持不变,表现为Gauss函数分布曲线随着列车轮载的移动而平移。
1.2 多个列车轮载作用的轨枕荷载分担比

图2 单列车轮载作用于轨枕正上方时的轮轨荷载分担比Fig.2 Load sharing ratio of sleepers with single wheel acting above the sleeper
列车荷载由多节列车车厢的轴载组成,可认为是多个轮轴荷载,由于轮轴间距通常不大,道床-路基结构内部的应力场需要考虑各轮轴之间的相互影响。图3所示为和谐号CRH3型电力动车组车厢结构示意图,由图3可见:1 个转向架中2 个轮轴的间距为2.5 m,前后车厢相邻转向架的前后轮轴间距为5.0 m。由于单列车轮载作用于轨枕正上方时由5根轨枕承担,影响长度为2.60 m;作用于2个相邻轨枕之间时由6根轨枕承担,影响长度为3.25 m。因此,1 个转向架的2 个轮轴荷载存在荷载影响叠加区,而前后车厢2个转向架之间不存在荷载的相互影响。
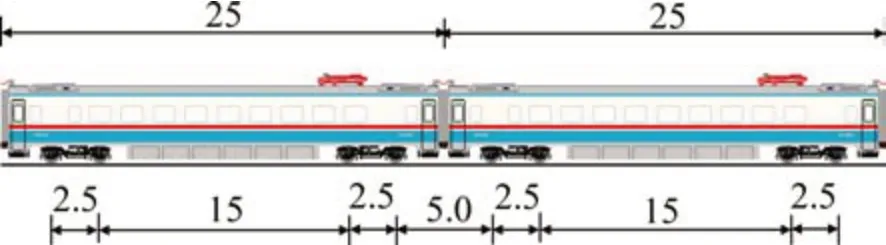
图3 CRH3车厢结构示意图Fig.3 Geometry of the CRH3 carriage
基于上述分析,对于CRH3 系列高速列车荷载,仅需研究1 个转向架的2 个轮轴荷载的作用,本文主要考虑如下的2种情况:1)其中有1个列车轮载位于2个相邻轨枕的中点处;2)其中有1个列车轮载恰好位于某一轨枕正上方。通过Gauss函数的叠加计算,可以分别计算2种情况下各轨枕的荷载分担比,计算结果如图4所示,其中,第1种情况下双轮轴荷载将由其影响范围内的10 根轨枕承担,而第2种情况下的列车轮载将由其影响范围内的9根轨枕承担。
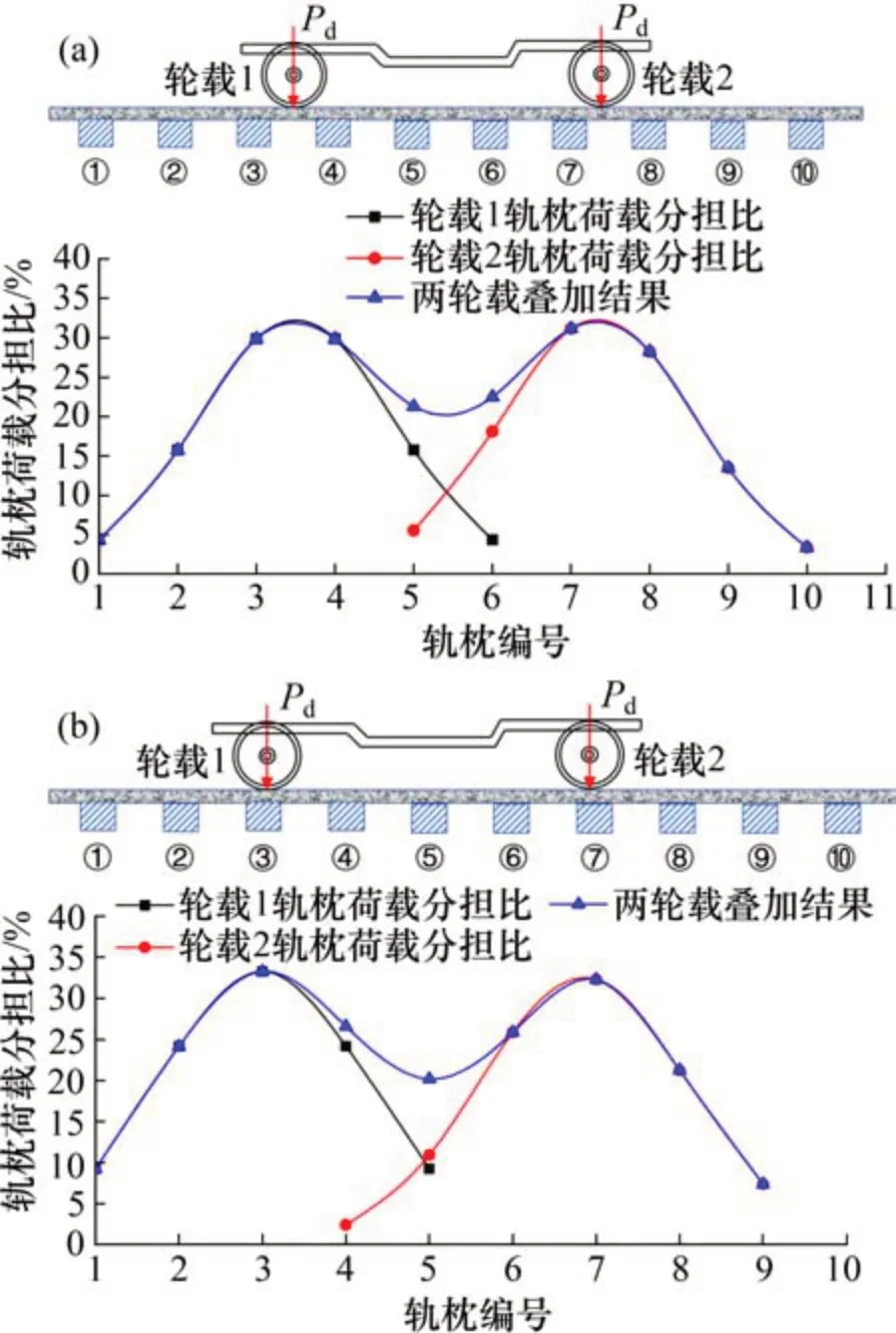
图4 双轮载作用于不同位置处的轨枕荷载分担比Fig.4 Load-sharing ratio of sleepers when two with loads acting on different positions of rail
由图4可知:在1 个转向架的2 个列车轮载作用下,轨枕荷载分担比沿转向架的中心呈对称分布,近似为“M”形。由于2 个轮载的相互叠加,导致转向架之间区域的轨枕所承担的荷载高于两侧轨枕承担的荷载,但轨枕分担比的最大值仍然位于列车轮载所作用的位置,且与单个列车轮载作用下的轨枕荷载分担比最大值相同,表明基于本文所考虑的列车荷载情况,轨枕荷载分担比的最大值没有受到相邻轴载的影响。同时可以看出,双轮载作用于不同位置所引起的轨枕荷载分担比不同,当荷载1位于相邻轨枕中心时,转向架之间范围内轨枕荷载分担比更为均匀,且最大轨枕荷载分担比相对较小。由于轮载1作用于轨枕正上方的情况所对应的轨枕荷载分担比最大,对于路基结构承载力设计更为不利。因此,后续研究将考虑第2种情况所示的双轮荷载作用位置。
1.3 道床表面的列车轮载分担规律
列车轮载依次由钢轨传递到轨枕、道床,最终传递到路基结构表面的应力在轨枕的有效支承面积内均匀分布[19],对于本文中的荷载工况,双轮轴作用下道床表面的荷载分布规律示意图如图5所示。图5中,b为轨枕的平均宽度;e为轨枕单侧的平均有效支承长度,一般取为轨枕端部至钢轨中轴线距离的2 倍,对于长度为2.6 m 的轨枕,轨枕单侧的平均有效支承长度e为1.1 m。
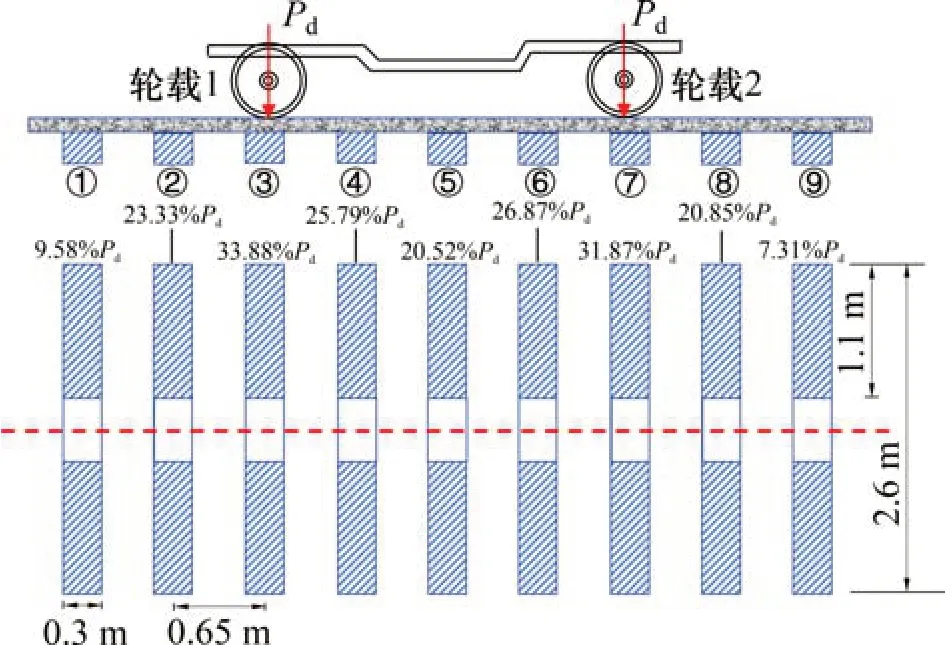
图5 双轮轴作用下道床表面的荷载分布规律示意图Fig.5 Load distribution on the ballast surface under two wheel loads
2 单层道床结构的静力安定解析方法
2.1 Melan静力安定定理
Melan安定定理也称为静力安定定理:若存在一个与时间无关的自平衡残余应力场σr ij,它与给定荷载范围内的任意外荷载λp(p为单位荷载,λ为无量纲因子)所产生的弹性应力场σe ij相叠加后,处处不违反屈服准则f(·),则结构是安定的,可表述如下:
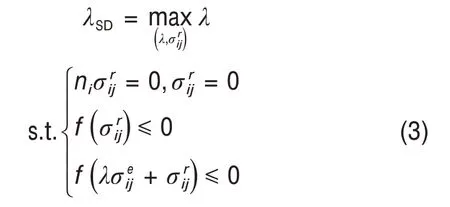
式中:λSD为静力安定荷载乘子,其中,第1 个表达式满足了残余应力场的自平衡条件,后2个表达式保证了弹性应力场与残余应力场的叠加满足屈服方程。
静力安定荷载求解的关键在于准确获得结构在外荷载作用下的弹性应力场以及构造与时间无关的最佳的自平衡残余应力场。弹性应力场可以通过弹性力学原理或数值模拟方法求解,而构造理想的残余应力场则相对较为困难。对于承受交通荷载作用的均质、各向同性半无限空间结构,YU[3]指出,由于其垂直于行车方向的截面受到相同的应力历史,因此,所有的残余应力分量均与交通荷载行驶方向(即x方向)无关,同时临界点始终位于xz平面(即y=常数),在此平面上,由于残余应力场的自平衡条件和边界条件,导致切应力因此,结构中可能存在的残余应力分量为和,且这2个分量是有关y和z的函数。由此,安定荷载的求解就最终归结为对残余应力场的优化和对弹性应力场的精确计算。
2.2 多轮载下半无限空间中弹性应力场解析方法
2.2.1 单个均布荷载产生的角点处弹性应力场
根据BOUSSINESQ 解,假设竖向均布荷载p作用于长和宽分别为A和B的矩形区域,若以矩形荷载的角点O为坐标原点建立直角坐标系,在矩形荷载面上任意取一面积为dxdy的微小单元,则作用于该微小单元上的分布荷载可以用集中力pdxdy表示,通过积分可以求得O点下方任意点M(0,0,z)处由竖向均布荷载所引起的弹性应力分量,如图6所示。

图6 均布荷载下半无限空间中弹性应力场计算示意图Fig.6 Elastic stress in half-space under uniform stress
在竖向均布荷载p作用下,沿O点以下任意深度处的弹性应力场推导结果为

由CERRUTI 弹性理论解,同样可以得到在水平均布荷载q作用下的弹性应力场,推导结果如下:


单个矩形均布荷载同时包含竖向荷载p和水平荷载q,且满足q=μp(假设作用于半无限空间结构中的水平向荷载与竖向荷载呈线性关系,比例系数为μ),则其在矩形荷载角点处产生的弹性应力场为

2.2.2 多个矩形均布荷载作用下的弹性应力场
假设第n个矩形荷载在半无限空间表面的角点坐标为(xn,yn,),则对于表面任意点O(x,y),根据其相对位置,可能出现如图7所示的4种情况。在计算中可以通过O点分别作平行于矩形均布荷载长边和短边的平行线,将面积划分成若干个区域,则O点就成为了各个区域的公共角点,分别计算每个矩形区域角点下同一深度z处的弹性应力场,然后,进行代数求和即可得到均布荷载作用于半无限空间任意深度处的弹性应力场。

图7 角点法计算弹性应力场的4种情况Fig.7 Four situations of corner points method for calculation of elastic stress field
对于多个均布荷载作用的情况,若荷载数为m,则由该m个均布荷载在半无限空间体内部任意点处产生的弹性应力场可以由叠加原理得到:

2.3 弹性应力场结果分析
列车轮载由钢轨和轨枕传递到道床表面的应力为均匀分布,且作用面积为轨枕的有效支承面积,单根轨枕的有效支承面积为2个大小相同的矩形荷载,与轨枕中心线呈对称分布。为简化分析,仅考虑半根轨枕的有效支承面积,分析弹性应力场。图8所示为单个轨枕作用于O点的弹性应力场示意图。考虑半根轨枕的有效支承为0.3 m×1.1 m(图8中虚影部分),分别施加100 kPa放入竖向和水平均布荷载,可得到O点以下z深度处的弹性应力场结果如图9所示。由图9可见:在单个荷载作用下,本文所推导的竖向应力的计算公式与土力学中的角点法完全一致。在半无限空间表面处,仅荷载作用区域范围abcd内有荷载存在,其他区域的所有弹性应力分量均为零,随着荷载向深处扩散,呈现出应力泡现象。因此,竖向应力沿O点先增大,然后减小,逐渐趋于零。

图8 单个轨枕作用于O点的弹性应力场示意图Fig.8 Elastic stress filed at point O under stress acting on single sleeper

图9 水平和竖直均布荷载作用下沿O点竖向应力计算结果Fig.9 Vertical stress along point O under horizontal and vertical distributed stress
考虑平面尺寸为3 m×3 m 的半无限空间结构,在其表面的中心区域施加如图8所示的呈平行分布2 个矩形均布荷载,沿y方向的间距为0.65 m,其中竖直和水平荷载均为100 kPa,则可得到如图10所示的深度z=0.5 m 处的各弹性应力分量计算结果。由图10可见:在2 个竖直与均布荷载作用下的弹性应力场相互影响,数值上相互叠加,且相对于2个荷载中轴线呈对称分布。由此可知:多个荷载作用所引起的弹性应力场必然在半无限空间结构中相互影响,而表现出与单荷载不同的弹性应力分布规律。因此,仅考虑单个荷载作用的安定分析不能准确反映结构的实际承载能力,必须针对结构的受力特点,考虑如图5所示的更为实际的荷载情况。
3 单层道床结构安定分析
考虑如图5所示的荷载分布形式,基于式(3),结合上述推导的均布荷载作用下半无限空间结构中的弹性应力场解析解,通过Matlab 编程可以求得单层道床结构的静力安定荷载λSD,安定荷载的具体求解过程及残余应力场的优化过程见文献[15]。
3.1 安定解析方法的验证
为了验证均布荷载作用下解析方法的正确性,本文考虑单个均布荷载作用,以归一化的静力安定荷载λSDp0/c作为分析内容,将计算结果与已有研究结果进行对比,结果如图11所示。由图11可见:本文的计算与SHIAU[20]基于均布荷载的计算结果规律基本一致,结果也较接近,最大误差为10%。由于有限元方法的离散性,所得到的安定荷载为精确安定荷载解的近似值[20],因此,本文存在的误差具有合理性,验证了计算方法的合理性与可靠性。
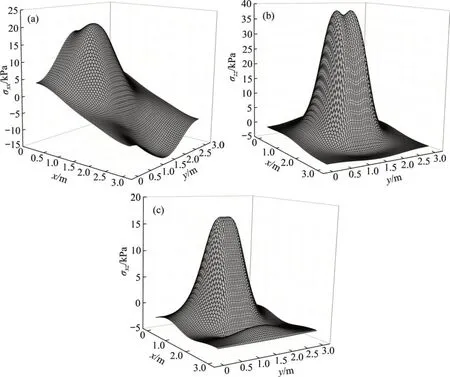
图10 2组竖直和水平均布荷载共同作用下的弹性应力场(z=0.5 m)Fig.10 Elastic stress field under two uniformly distributed horizontal and vertical stresses(z=0.5 m)
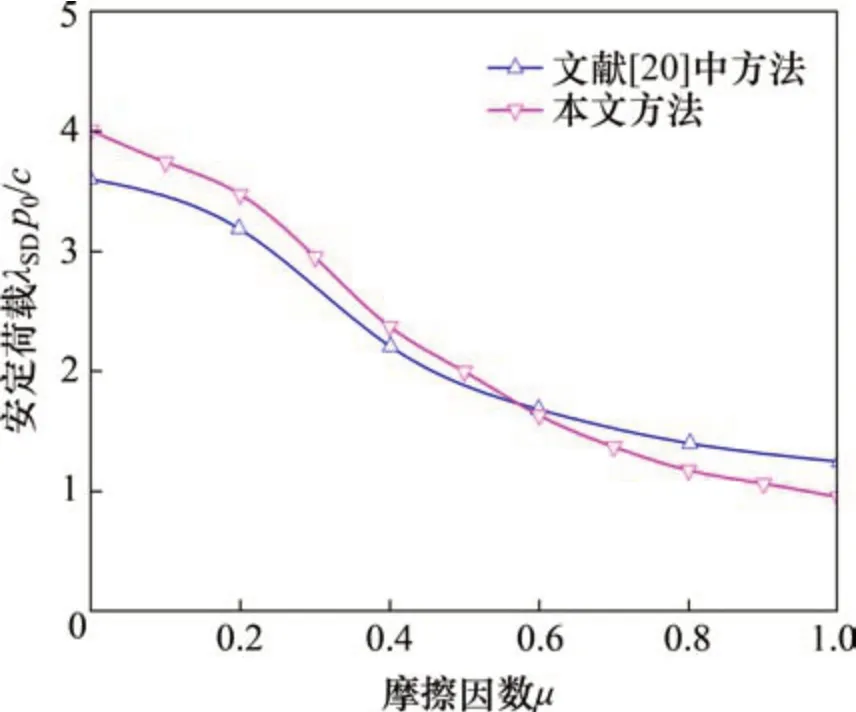
图11 均布荷载作用下的静力安定解析方法的验证结果Fig.11 Validation of the lower-bound shakedown solution under uniform stress
3.2 参数敏感性分析
假设道床材料服从Mohr-Coulomb 屈服准则,基于本文推导的均布荷载作用下的弹性应力场的求解方法可计算单位荷载p0作用下的弹性应力场,由Melan静力安定分析方法经简单的数值规划,可求解得到单层半无限空间结构的静力安定荷载乘子λSD。需要注意的是,本文中单位荷载p0为作用于图5的9根轨枕等效作用面积内的荷载总和,通过不同的荷载分担比计算得到相应轨枕等效作用面积上所承担的荷载。对于道床材料,在安定计算中考虑内摩擦角φ为45°,黏聚力c为5 kPa,泊松比v为0.3。为了尽可能全面分析道床材料的安定行为,本文分析了安定荷载的参数敏感性,选取道床内摩擦角φ的变化范围为25°~75°,泊松比v变化范围为0.10~0.49,归一化的静力安定荷载λSDp0/c计算结果如图12所示。

图12 道床材料参数对静力安定荷载的影响规律Fig.12 Influence of material properties of ballast on static shakedown load
由图12(a)可见:在给定的摩擦因数μ下,随着道床内摩擦角φ增大,静力安定荷载λSDp0/c几乎呈指数函数增长,对于μ=0的情况,道床内摩擦角由25°增大到75°导致道床结构的静力安定荷载增大了7.25 倍,说明材料内摩擦角增大可明显提高结构的承载能力。摩擦因数μ与作用在道床表面的切向荷载紧密相关,当μ增大时,结构所承担的荷载也相应增大,因此,摩擦因数μ降低了结构的静力安定荷载,当摩擦因数由0 增大到0.5 时,道床结构的静力安定荷载减小75%~88%。
由图12(b)可知:当摩擦因数μ≤0.2时,静力安定荷载随着泊松比增大而增大,当μ>0.2时,静力安定荷载随着泊松比增大而减小,但总体变化幅度均在1%以内,表明尽管泊松比v是弹性应力场的重要参数,但其对道床结构静力安定荷载的影响相对较小。
4 结论
1)对于CRH3系列高速列车荷载,仅在1个转向架的2个轮轴荷载之间存在叠加影响,在其影响范围内轨枕荷载分担比呈现“M”形分布。
2)通过与已有文献计算结果的对比,验证了本文推导的弹性应力场解析方法及静力安定分析方法的可行性和计算结果的准确性,可为安定理论在具体工程实际中的推广应用提供参考和理论依据。
3)道床结构的静力安定荷载随内摩擦角增大而增大,尽管泊松比是影响结构弹性应力场的重要参数,但其对道床安定荷载的影响较小,在满足经济性的前提下,适当选用高强度的材料,能有效提高给定摩擦因数下道床结构的承载能力。
