混凝土泵送管道振动监测与分析

(华中科技大学土木工程与力学学院，湖北武汉，430074)

混凝土泵送管道是泵送施工系统中输送混凝土材料的重要载体，在混凝土泵送过程中，由混凝土泵液压系统产生的泵压会对泵送管道产生较大的冲击和压力，导致泵送管道产生振动[1-2]。在实际泵送过程中，由于泵送压力、泵送管道的支撑方式和位置、管线布置以及混凝土性能等因素的影响，混凝土泵送有时会发生堵管、泄露和爆管等现象[3-5]，这直接影响项目的施工进度，甚至引发安全事故。姚煜中[6]研究表明，压力脉动流体的工作状态与输送管道的动力特性直接相关。因此，泵送管道的动力特性是反映混凝土泵送状态的重要参数，而通常加速度是结构动态信号测量和分析的主要物理参数之一[7-8]。目前有关混凝土泵送动力特性的研究主要集中在混凝土泵车臂架[9-11]，对混凝土泵送管道的动力特性监测及分析的研究极少，而利用加速度传感器可以获取土木工程结构的振动位移及振动频率等动力特性，实时掌握结构的工作状态变化[12]，及时发现结构工作时的异常状态。因此，本文通过监测混凝土泵送时管道振动加速度，分析混凝土泵送管道振动的动力特性和变化规律，有利于及时发现混凝土泵送的异常状态和采取措施防范堵管、漏管等现象，对保证混凝土正常泵送具有很重要的理论和工程实际意义。

1 混凝土泵送管道现场监测方案

1.1 混凝土泵送管道现场监测系统

选择武汉市光谷广场附近某栋58 层的在建高层住宅混凝土泵送管道系统进行监测，泵送管道加速度监测时混凝土已浇筑到第10 层，混凝土泵选用中联重科生产的ZLJ5180THBJE-10528R 型混凝土车载泵。泵送试验监测系统主要由测试系统、数据采集和数据存储3部分组成。加速度传感器采用1A116E型压电式加速度传感器，数据采集采用DH3822型动态信号采集系统。混凝土泵送管道振动加速度监测现场和监测系统如图1所示。

图1 混凝土泵送管道振动加速度监测现场和监测系统Fig.1 Monitoring site and system of vibration accelerate of concrete pumping pipe

1.2 管道振动加速度测点布置

选择第1层水平直管段、水平弯管和第1层竖直管段和竖直弯管进行加速度测试。加速度测点布置如图2所示，控制截面选在各管道中间部位。在每个控制截面布置2 个相互垂直的加速度传感器，将管道2个相互垂直的方向分别定义为X方向和Y方向，如图3所示。

2 混凝土泵送管道振动分析

2.1 加速度去噪处理和振动位移计算原理

2.1.1 加速度信号去噪处理

现场试验采用的是直流电源，采集到的加速度振动信号包含了其直流信号和周围环境噪声，因此，须对原始信号进行去噪处理。对采集到的数据信号进行合理的滤波处理，可以起到降噪的作用，有利于准确识别监测结构的状态[13]。近年来，许多滤波技术已应用于结构体监测数据的去噪处理[14-17]。考虑到本试验加速度传感器的幅频变化特性，切比雪夫II型滤波器在通带内具有更稳定的幅度函数和衰减特性[18-19]，对本试验原始数据处理获取有效数据更有优势。因此，本研究采用IIR切比雪夫II 型数字滤波器对加速度信号进行去噪处理。

2.1.2 管道振动位移计算原理

对采集的加速度信号进行时域积分处理，获取泵送管道的振动速度和振动位移。试验采集的泵管振动加速度a(t)含有直流干扰成分η，即a(t)=a1(t)+η，则振动速度和振动位移分别为

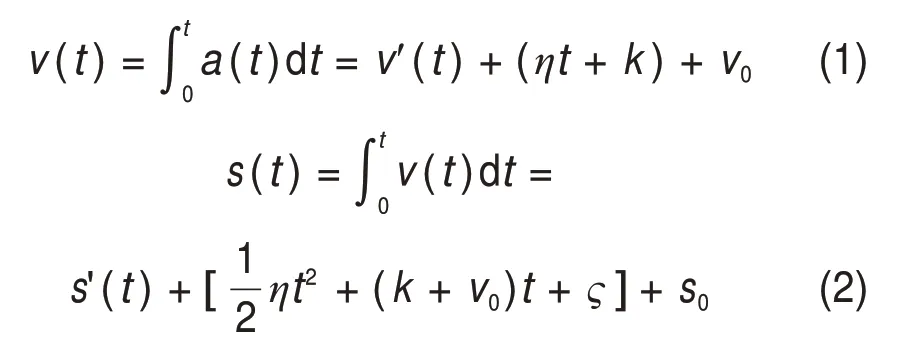
式中：v0为初始速度，v′(t)为v(t)的原函数；s0为初始位移，s′(t)为s(t)的原函数；k和ς分别为η在一次积分和二次积分后得到的积分常量。

由于直流分量η的影响，导致由加速度积分得到的速度曲线有ηt+k+v0趋势项，同样加速度经过二次积分后，位移曲线的趋势项为+(k+v0)t+ς+s0，积分结果中的趋势项误差积累会引起波形变形，这对位移曲线的准确性有较大影响[20]。因此，本研究对速度和位移信号曲线多项式采用最小二乘法进行波形修正，消除加速度积分过程中产生的趋势项误差，从而得到更为精确的振动速度和振动位移信号[21-22]。

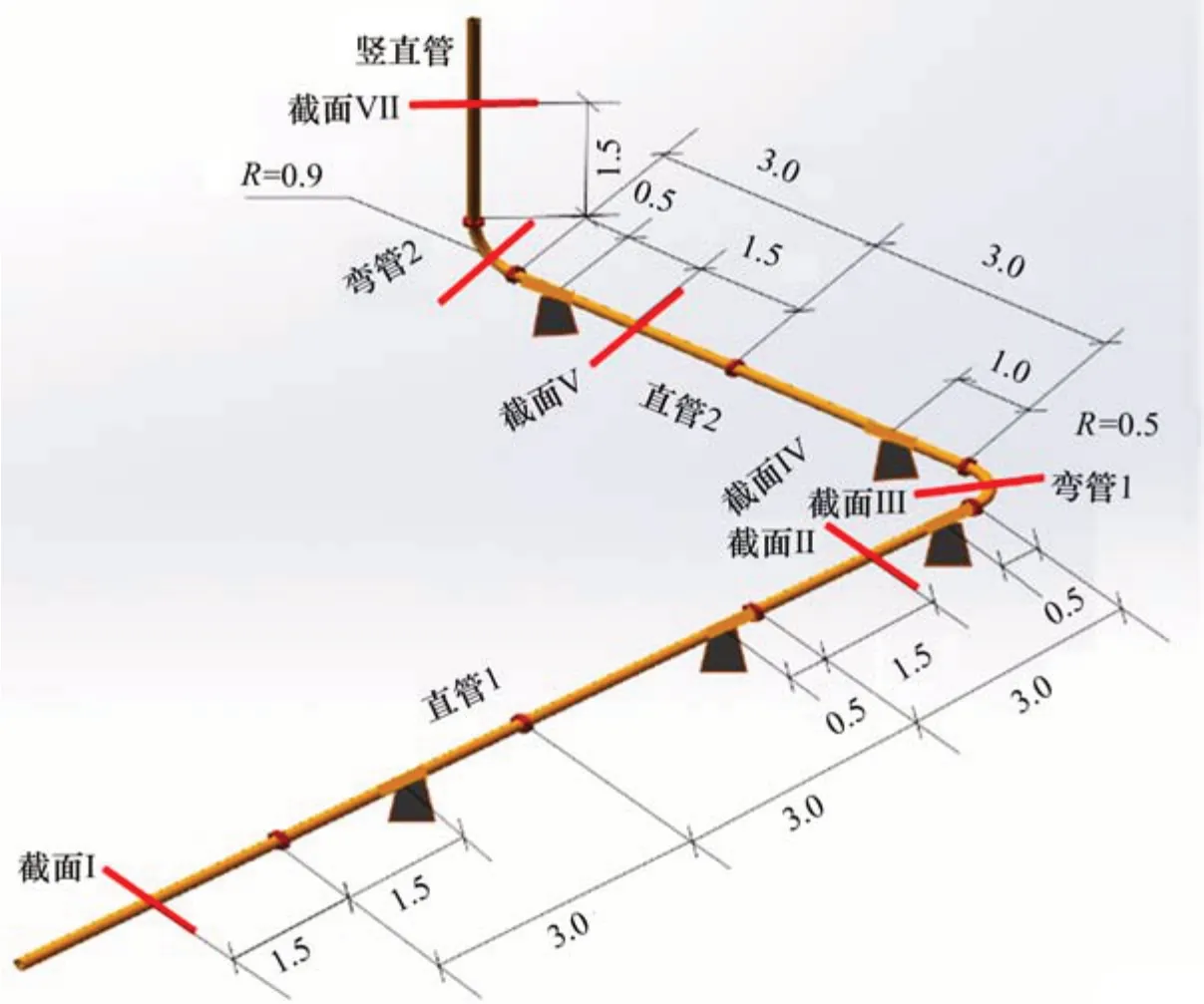
图2 泵送管道振动加速度测试控制截面Fig.2 Control sections of vibration acceleration test of concrete pumping pipe

2.2 不同泵送阶段管道加速度监测与分析

2.2.1 泵启动阶段

混凝土控制截面的最大加速度反映了该部位的振动响应，图4所示为试验采集的泵启动阶段不同泵压下各控制截面最大振动加速度。由图4可见：控制截面I 处X和Y方向加速度最大，因为混凝土泵启动时管内混凝土运动状态发生突变，而截面I离泵源最近，受到泵的冲击作用相对其他截面大，管道因此突然产生剧烈振动。除弯管截面III 处X方向和弯管截面VI 处Y方向最大加速度有突增现象外，随着管道长度延伸，管道振动加速度逐渐减小。

2.2.2 正常泵送阶段

对泵压20 MPa 时离泵源最近的水平直管段截面I和最远的竖直管段截面VII的X和Y方向加速度数据进行滤波处理，得到截面I和截面VII的X和Y方向加速度，如图5所示。由图5可见：正常泵送阶段管道截面I 处X和Y方向加速度峰值变化的周期性不明显，而截面VII 的X和Y方向加速度变化具有较明显的周期性，且加速度稳定在[-0.3g，0.3g](g为重力加速度)区间内。

图3 泵送管道振动加速度传感器布置方向示意图Fig.3 Arrangement direction of acceleration sensor of concrete pumping pipe

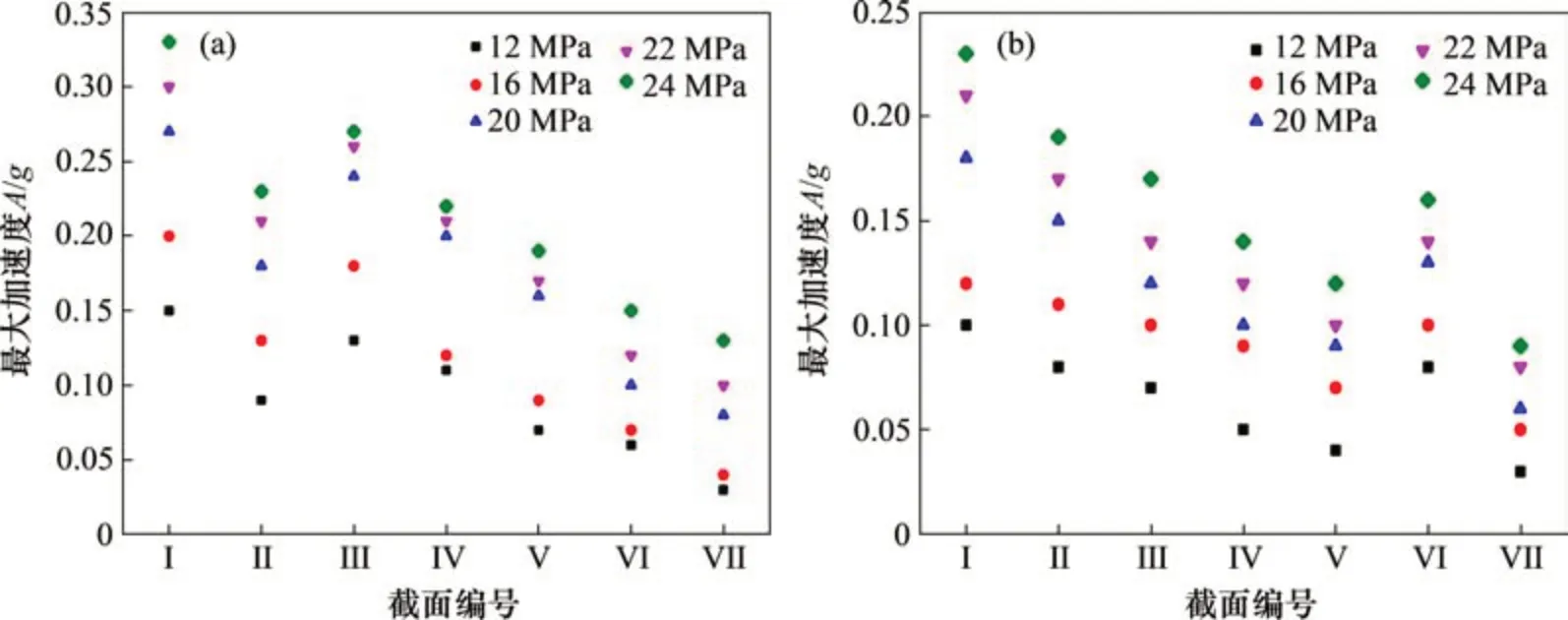
图4 各控制截面最大振动加速度Fig.4 Maximum vibration acceleration of each control sections

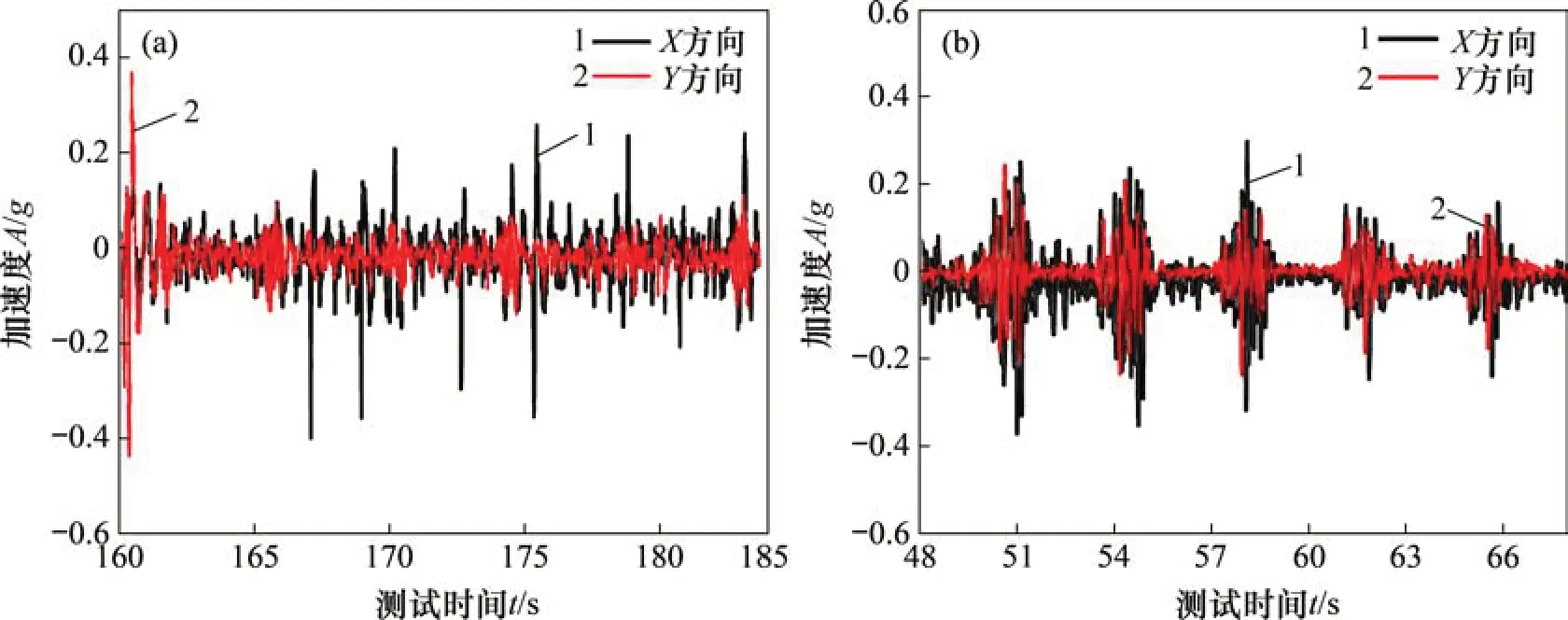
图5 正常泵送阶段不同控制截面振动加速度Fig.5 Vibration acceleration of different control section

分析不同条件下加速度峰值的出现时间，发现管道的振动加速度周期性随着管道延伸明显加强。对一定时间间隔内泵管振动的加速度进行峰值提取并记录峰值出现的时间，将相邻2个加速度峰值出现的时间点相减得到相应的加速度峰值周期Ti，

式中：ti和ti+1分别为泵管振动加速度的第i个峰值和第i+1个峰值出现的时间。

对一段测试时间内获取的泵管振动加速度峰值周期Ti进行算数平均计算，得到该组加速度数据峰值出现的周期T,

式中：n为在一定时间间隔内加速度峰值周期Ti的总数。

分析20 MPa 泵压下加速度，得到各截面峰值平均周期如图6所示。由图6可见：管道不同截面的振动加速度峰值周期随管道的延伸趋于稳定，在水平直管截面I 处X和Y方向加速度峰值出现周期比其他截面的小，表明泵送过程中该管段振动比较复杂，因而加速度峰值出现较多。经过弯管，从截面III 开始后面截面加速度峰值周期基本稳定在4.3 s 左右，与混凝土泵的行程转换时间基本一致。分析不同泵压下各截面X和Y方向的峰值周期，发现其周期变化规律与上述规律一致。

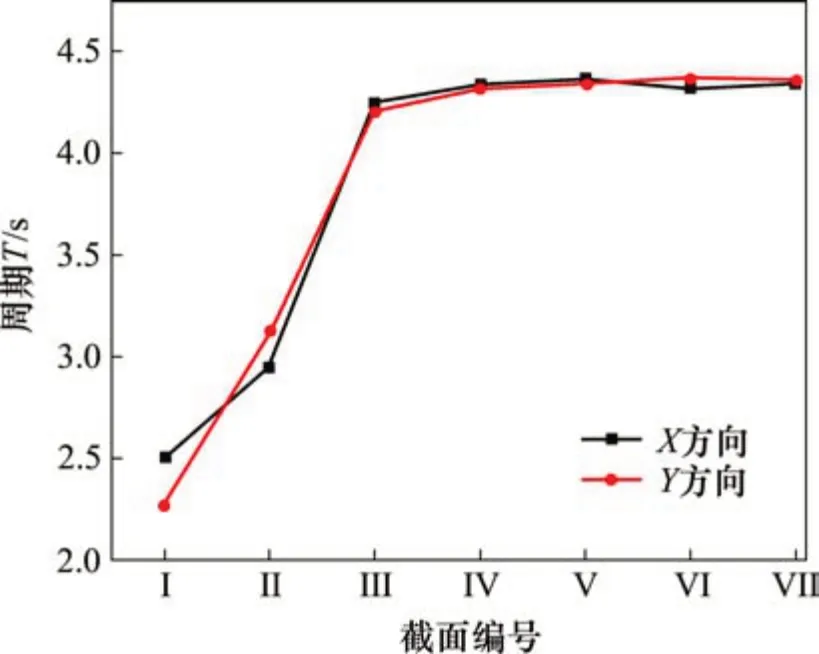
图6 不同截面X和Y方向加速度峰值出现周期Fig.6 Period of peak acceleration in X direction and Y direction

2.3 混凝土泵送管道振动位移分析

2.3.1 泵压20 MPa下管道振动位移结果与分析

振动位移能更直观地判断管道运行状态，因此，选取20 MPa 泵压下正常泵送过程中的加速度曲线进行二次积分和去趋势项处理，得到各截面X和Y方向的振动位移，如图7所示。

由图7可见，在水平直管截面I 处X方向最大振动位移达到15 mm，Y方向最大振动位移仅5 mm，X方向振动位移明显大于Y方向位移，且该截面振动最剧烈，这主要是因为截面I 离泵源最近，混凝土泵送压力损失较小。截面III、截面IV和截面V 的振动位移在2～5 mm，竖直管段振动位移保持在2 mm左右。试验表明经过弯管后管道振动大幅减弱，且以水平振动为主，随着管道延伸，振动位移逐渐减小。这主要因为在正常泵送过程中，混凝土输送经过一段距离的直管和弯管后，混凝土压力衰减幅度减小并趋于稳定，管道振动随之减弱。

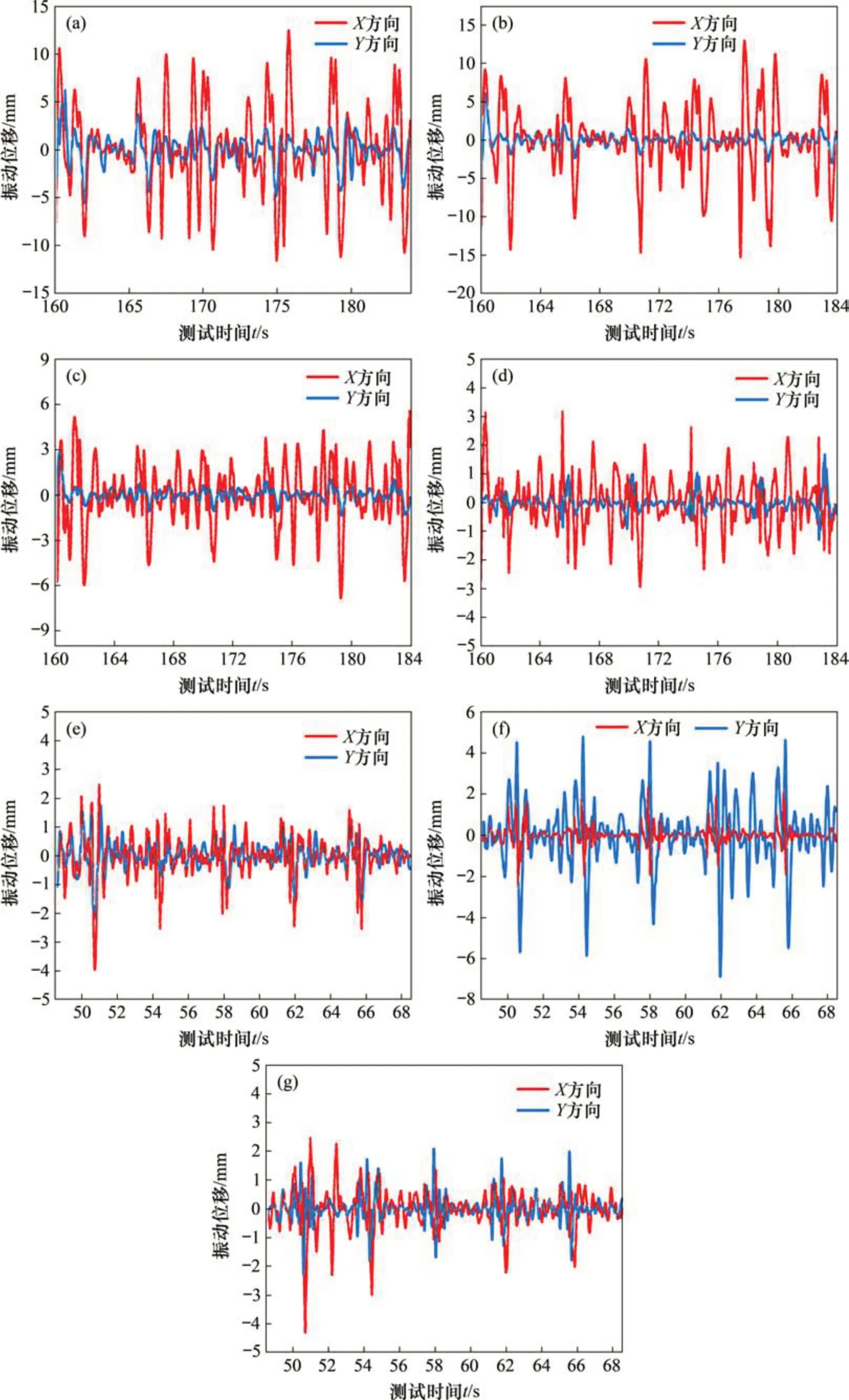
图7 各控制截面振动位移变化Fig.7 Vibration displacement of each control section

2.3.2 不同泵压下管道振动位移

采用同样方法对不同泵压下采集的加速度曲线进行二次积分和去趋势项处理，得到不同泵压下各控制截面X方向的平均最大位移如图8所示。由图8可见：不同泵压下，混凝土泵送管道振动位移的变化规律是一致的，泵压越大，管道振动位移越大。第1段水平直管X方向振动位移最大，经过第1段水平弯管截面III及以后截面X方向的振动位移缓慢减小并趋于稳定，且X方向振动位移都在4 mm以内。

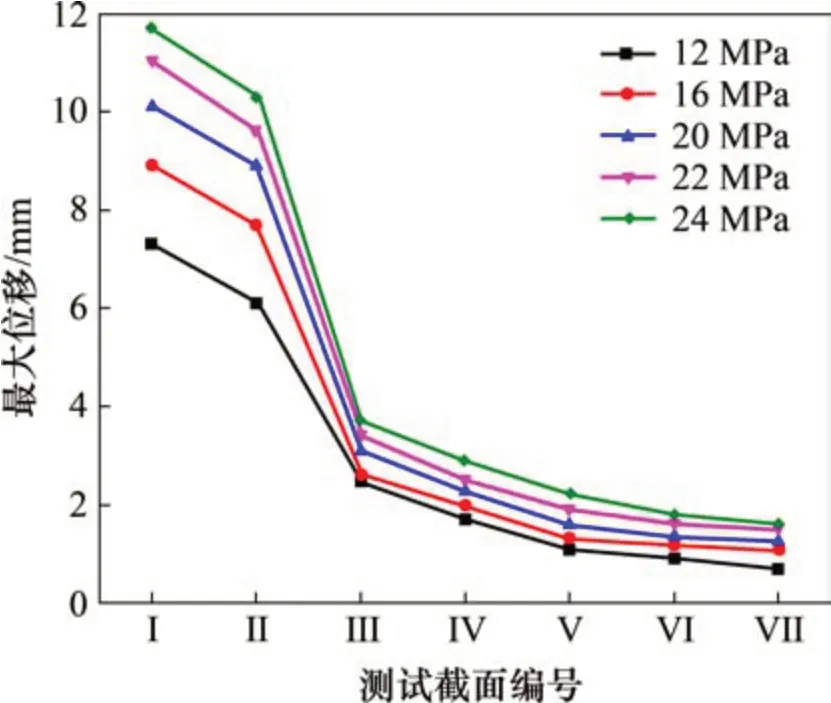
图8 各控制截面X方向最大振动位移Fig.8 Maximum vibration displacement in X direction of each control section

分别将泵压与不同截面X方向振动位移进行拟合，得到各管段截面X方向振动位移与泵压的关系，如图9所示。

从图9可以发现，同一管段截面X方向振动位移与泵压呈线性关系，因此将直线的斜率定义为管段X方向位移特征系数λx，表征不同泵压下管段X方向振动位移变化，将直线截距定义为管道X方向位移常数Bx，则X方向振动位移方程式为

式中：Sx为管道X方向振动位移；P为混凝土泵源泵压。

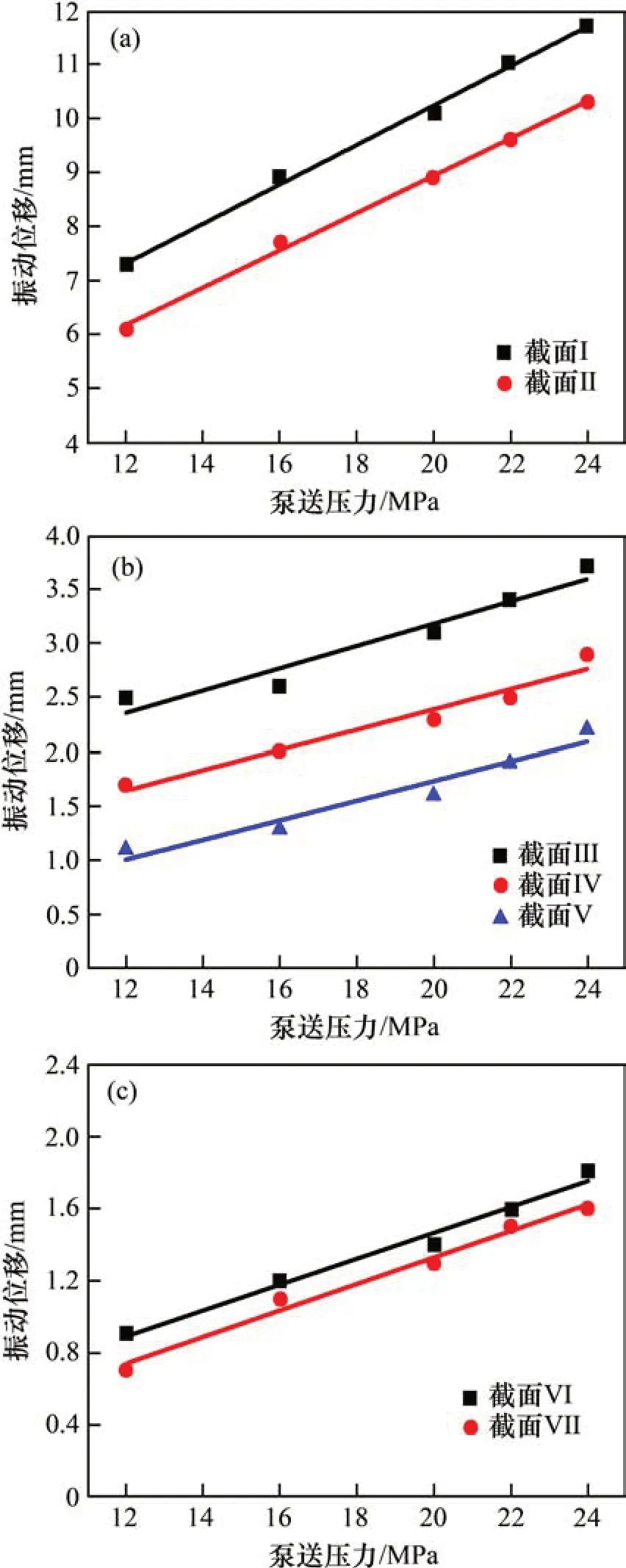
图9 不同泵压下泵送直管振动位移Fig.9 Vibration displacement of straight pumping pipe under different pumping pressures

分别对不同管段进行拟合分析计算，得到第1段水平直管λx1为0.353，第2 段水平管λx2为0.095，竖直管段λx3为0.073。研究表明：管道振动位移与泵压呈线性关系，λx可以表征截面X方向振动位移的变化，不同管段λx不同，离泵源最近的第1段水平管λx最大，经弯管后λx突然减小，之后λx衰减可以忽略，同一管段不同截面位移常数Bx不同。

3 结论

1)在泵启动阶段，靠近泵源的水平直管振动加速度最大，垂直于弯管外弧线方向的加速度有突增现象，泵送管道其余截面加速度随着泵送管道延伸逐渐减小。

2)在正常泵送阶段，泵压越大，则泵送管道振动最大加速度越大，靠近泵源处泵送管道振动加速度周期性不明显，但随着泵送管道延伸，泵送管道振动加速度变化的周期性明显加强。

3)同一泵送管段截面X方向振动位移与泵压呈线性关系，泵压越大，泵送管道振动位移越大。泵送过程中第1段水平直管振动位移最大，经过弯管后泵送管道振动位移大幅降低，且泵送管道振动以X方向为主，Y方向振动相对较小。

4)X方向位移特征系数λx可以表征不同泵压下泵送管段X方向振动位移变化，离泵源最近的第1段水平管λx最大，经弯管后λx突然减小，之后λx衰减很小可忽略；同一泵送管段不同截面位移常数Bx不同。