一种半监督人脸数据可分性特征提取方法∗

刘 敬 刘鑫磊 刘 逸

（1.西安邮电大学电子工程学院 西安 710121）（2.西安电子科技大学电子工程学院 西安 710071）

1 引言

近年来，人脸识别［1～2］技术是一个研究热点。人脸数据与普通数据相比，具有超高维小样本的特点。由于人脸数据维数过高，常达几千上万维；而样本个数常为几十个，与维数相比过低，使得人脸数据处理起来比较困难。

通常在采用人脸数据进行分类之前需要对原始数据进行特征提取，以降低维数并提高人脸识别效率，因此人脸数据的特征提取技术也越来越多。矩阵分解［3］是一种非监督学习技术，从数据中提取一组特征基向量，并从中获取高级语义。从最近的机器学习和稀疏编码［4］的发展中，稀疏概念编码（Sparse Concept Coding，SCC）［5］是近年兴起的一种矩阵分解方法，SCC 首先学习一组能够捕捉数据内在流形结构的基向量；然后以这组基向量为字典［6］进行稀疏表示学习。因此，SCC 所得稀疏表示既保留了数据的几何结构，又具有稀疏表示的优点，即具有更好的可分性和稀疏性。SCC 属于非监督学习，在语义结构上有较好的代表性，常用于聚类。由于学习过程中没有考虑类标，因此数据在SCC子空间的可分性不是很强，直接在SCC子空间进行分类并不能显著提高识别率。

数据的可分性特征提取技术，是指通过某种变换将原始数据映射到低维特征子空间，使得数据在该低维子空间获得较好的可分性。可分性特征提取方法常用于人脸识别领域，可降低维数，提高分类识别率和分类速度。基于Fisher［7］准则的线性判别分析（Linear Discriminant Analysis，LDA）［8］是经典的可分性特征提取方法，LDA将高维的原始样本投影到低维LDA 特征子空间，使得在子空间中数据的类间散布与类内散布之比最大。LDA 属于监督学习，故LDA 不能利用无类标的样本，即LDA 不能提取出包含在无类标的测试样本中的可分性信息。人脸识别属于超高维小样本问题，采用LDA直接对人脸数据训练样本进行特征提取，存在以下问题：1）训练样本过少，造成类内散布矩阵奇异，无法求解；2）无法利用无类标样本，即不能提取出无类标样本中的可分性信息；3）原始数据维数过高，使得特征提取速度慢；4）单一的可分性特征提取方法，导致效果不理想，数据在LDA 特征子空间识别率较低。

为提高人脸数据的识别率和识别速度，本文提出一种结合SCC 和LDA 的人脸数据半监督可分性特征提取方法——SCC-LDA。SCC-LDA 先采用SCC 获取保留人脸数据固有空间几何结构的低维稀疏表达；然后采用LDA 在SCC 子空间进行有监督特征提取，进一步提取数据的可分性特征并降维。SCC-LDA 相当于对数据进行了两次特征提取，运算时间较LDA 有明显缩短，且特征子空间中数据的可分性更强。SCC-LDA 将非监督学习与监督学习相结合，相比LDA：1）可由SCC 的字典学习过程捕获人脸图像的固有流形结构，故相比LDA子空间，SCC-LDA 子空间包含了更多分类信息；2）相比LDA 对原始高维数据进行特征提取，SCC-LDA 采用LDA 对保留人脸数据固有空间几何结构的SCC低维稀疏表达进行特征提取，不仅进一步提取了可分性信息，还可提高人脸特征提取速度，进而提高人脸识别速度。本文采用K 近邻（K-Nearest Neighbor，KNN）［9］分类器和最小距离（Minimum Distance，MD）［10］分类器验证特征提取的有效性。基于ORL 和Yale 数据的实验结果表明，相比SCC 子空间法和LDA 子空间法，本文所提SCC-LDA 子空间法可显著提高识别率，并可加快人脸识别速度。

2 稀疏概念编码

SCC 首先通过捕捉数据的内在流形结构，学习一组保留数据流形结构的基向量；然后以这组基向量为字典进行稀疏表示学习。所得低维稀疏表示既保留了数据的几何结构，又有更好的可分性且为稀疏的。

2.1 稀疏表示基向量学习

SCC 首先学习稀疏表示的基向量，即字典学习。SCC 为获取能保留数据潜在流形结构的基向量，先用流形学习［11］进行图谱分析［12］，用图谱逼近流形，得到隐藏在高维空间中样本的低维流形嵌入，然后学习保留此流形嵌入的SCC基向量。

具体先用K 近邻法构建邻接图G，图中的N个顶点与每个样本一一对应，边为每个样本与其K近邻之间的相似度，为局部几何模型定义权重矩阵W，且

其中NK(xi)表示xi的K 近邻集合。则图拉普拉斯矩 阵 L=D-W，其 中 D 为 对 角 矩 阵 且。为捕获嵌入在高维空间中的低维数据流形，求解下面的广义特征值问题［13］：

其中Y=[y1y2…yk]，yi是上述广义特征值问题特征值由小到大排序对应的特征向量，Y 的每行是各样本在k 维子空间中的流形嵌入。为保留数据流形结构，SCC 学习保留低维流形嵌入Y 的字典U，U 的各列为SCC 的基向量，可通过求解下式的最优化问题完成：

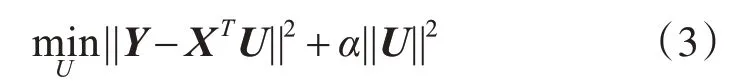
其中，X 为样本矩阵，原空间各样本存储在X 各列，α 是正则化参数，α||U||2调整模型以避免过学习。通过上式对U 的求导，令导数为零，可求得最优解：

I 为单位矩阵。也可以通过LSQR［14］方法直接算出U*。

由式（3）可知，SCC 的基向量保留了数据的流形结构，原始数据投影到SCC 基向量后，与数据的流形嵌入最接近。

2.2 稀疏表示学习

在获得SCC 基向量矩阵U 后，稀疏表示A 的各列可通过求解下面的最小化问题计算：

xi和ai分别是X 和A 的各列，A 的各列为X列中对应样本的稀疏表示，| ai|表示ai的L1范数，L1范数正则化项可以确保ai的稀疏性。上式有以下等效公式：

通过式（6）将SCC 子空间中U 的系数稀疏化，所得稀疏表示A 是稀疏的。最小角回归（Least Angle Regress，LARs）［15］算法可以解决这类最优化问题，LARs 算法通过设定ai的非零分量个数来控制ai的稀疏性，无需设置参数γ。

SCC 可将数据降维，并在通过SCC 的基向量获取数据稀疏表示的同时，保留了数据固有的空间几何结构。

3 线性判别分析

LDA 寻找一个最佳判别投影矩阵V，使样本投影到LDA 特征子空间中后Fisher 准则最大，即LDA 子空间中类间散布与类内散布之比最大。Fisher准则函数：

其中，Sb和Sw分别为原始数据的类间散布矩阵和类内散布矩阵。采用LDA 对训练样本进行特征提取，首先计算训练样本数据的类间散布矩阵Sb和类内散布矩阵Sw：

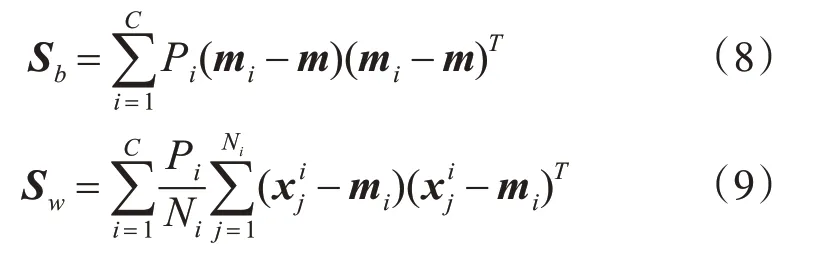
其中，C 表示样本的类别数，Pi表示第i 类的先验概率，可通过该类训练样本个数除以训练样本总数估计得到，即Pi=Ni/N，N 表示训练样本总数；Ni表示第i 类训练样本数；mi表示第i 类训练样本的均值，表示第i 类的第j 个训练样本；m 表示训练样本的整体均值向量，

通过Fisher准则函数求解最佳投影矩阵：

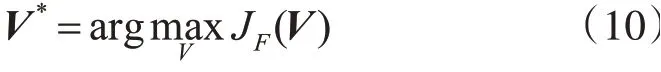
若LDA 子空间的维数为m，则LDA 的解V*各列为前m 个最大特征值对应的特征向量。将原空间样本映射到LDA 特征子空间，得到映射后的样本集Z ：

4 SCC-LDA人脸特征提取

针对人脸数据维数高，可分性差的问题，本文提出一种新的半监督人脸数据可分性特征提取方法——SCC-LDA，可提高人脸识别效率。SCC-LDA 首先对所有样本，包括有类标的训练样本和无类标的测试样本，采用SCC进行无监督的稀疏学习，稀疏学习包括基向量的学习和稀疏表示的学习，在降低数据维数的同时获取数据的保留流形结构的稀疏表示，且所得稀疏表示包含了来自所有样本的分类信息；然后采用LDA 在SCC 稀疏表示子空间进行有监督的可分性特征提取，分类识别在所得SCC-LDA子空间进行。

SCC-LDA 的人脸特征提取算法具体步骤如下。

1）将原始n 维空间的人脸数据集X 划分为训练样本集Xtr和测试样本集Xte，各样本xi∈ℜn×1均按列存放；

2）将所有样本X，包括训练样本集Xtr和测试样本集Xte，采用SCC进行稀疏表示学习和降维：

（1）采用式（1）构造权重矩阵W，根据流形学习求解式（2）得到所有样本的低维流形嵌入Y，再通过学习一组保留人脸图像流形结构的基向量，并以列存放在基向量矩阵U∈ℜn×p中，p 为SCC子空间的维数，且p＜n；

3）采用LDA 对SCC 子空间中训练样本的稀疏表示集Atr进行特征提取和降维，将求得的特征向量 以 列 存 放 在 投 影 矩 阵V∈ℜp×m中，m 为SCC-LDA子空间的维数，且m＜p＜n；

4）将训练样本的稀疏表示集Atr和测试样本的稀疏表示集Ate，分别采用Ztr=VTAtr和Zte=VTAte投影到SCC-LDA 子空间，Ztr和Zte分别为SCC-LDA 子空间的训练样本集和测试样本集。最终，分类识别在SCC-LDA子空间进行。

本文在SCC-LDA 子空间采用KNN 和MD 分类器进行分类识别，以评估所提特征提取方法的有效性。KNN 分类器决策规则为，对于SCC-LDA 子空间的任一测试样本zte，判决zte属于所决定的类，其中ki表示zte的K 近邻中属于第i 类的训练样本数。MD分类器以各类均值为模板建立模板库， 判 决属 于所决定的类，其中表示zte和第i 类均值模板的欧式距离。

本文提出的SCC-LDA 方法对人脸数据进行了两次特征提取，首先采用SCC 进行非监督特征提取，然后在SCC 稀疏表示子空间采用LDA 进行监督特征提取。SCC-LDA 将非监督学习与监督学习相结合，可由SCC的字典学习过程保留人脸图像的固有流形结构。故SCC-LDA 子空间，相比SCC 子空间有更强的可分性；相比LDA 子空间包含了无类标样本的分类信息，人脸识别速度也有显著提高。

5 实验结果

为验证本文所提SCC-LDA 算法的有效性，分别采用KNN、MD 分类器对ORL_32×32、ORL_64×64、Yale_32×32、和Yale_64×64 四组人脸数据［16］进行分类，并分析比较SCC 子空间法［17］、LDA 子空间法、所提SCC-LDA 子空间法的平均识别率、Kappa［18］系数和运行所用时间。Kappa 系数为计算分类精度的方法，可分为五组来表示不同级别的一致性：0～0.20 极低的一致性（slight）、0.21～0.40 一般的一致性（fair）、0.41～0.60 中等的一致性（moderate）、0.61～0.80高度的一致性（substantial）和0.81～1几乎完全一致（almost perfect）。四组人脸数据的实验结果均表明，本文所提SCC-LDA 子空间法，相比SCC子空间法和LDA 子空间法，可显著提高人脸识别率；相比LDA子空间法可显著提高人脸识别速度。

仿真环境：操作系统为Windows 7，CPU 为2.50GHz，内存为6.0GB，编程平台为Matlab R2014a。

5.1 人脸数据介绍

本文采用ORL 和Yale 人脸数据库，ORL 人脸库由40 人组成，每人10 幅，Yale 人脸库由15 人组成，每人11 幅。ORL_32×32 和Yale_32×32 中为32×32 像素的图像，ORL_64×64 和Yale_64×64 中为64×64 像素的图像，对这四个人脸数据库［16］均分别随机选取每人的5、6、7 张图像作为训练样本，其余作为测试样本。

5.2 实验结果分析

表1 为分别用MD 分类器和KNN 分类器对ORL_32×32 人脸数据，在各类训练样本数为5、6、7的情况下进行20 次分类，统计出的平均识别率、平均Kappa系数、和运行时间。

从表1 中可以看出，两种分类器在各类训练样本数为5、6、7 时，本文所提SCC-LDA 方法的平均识别率，相比SCC 法和LDA 法，均有显著提高，同时识别率标准差最小，Kappa 系数最大；SCC-LDA法的运行时间较LDA 有显著缩短。以各类训练样本数为5 为例，MD 分类器SCC-LDA 平均识别率比LDA 高出7.65 个百分点，比SCC 高出5.70 个百分点；KNN 分类器SCC-LDA 的平均识别率比LDA 高出8.58个百分点，比SCC高出6.85个百分点。各类训练样本数为6和7时，效果也同样明显。

表1 ORL_32×32数据MD、KNN分类器的识别率Kappa系数和运行时间

表2 ORL_64×64数据MD、KNN分类器的识别率Kappa系数和运行时间

表2 为分别用MD 分类器和KNN 分类器对ORL_64×64 人脸数据，在各类训练样本数为5、6、7的情况下进行20 次分类，统计出的平均识别率、平均Kappa系数和运行时间。

从表2 中可以看出，两种分类器在各类训练样本数为5、6、7 时，本文所提SCC-LDA 方法的平均识别率，相比SCC 法和LDA 法，均有显著提高，同时识别率标准差最小，Kappa 系数最大；SCC-LDA法的运行时间较LDA 有显著缩短。以各类训练样本数为5 为例，MD 分类器SCC-LDA 平均识别率比LDA 高出8.3%，比SCC 高出7.6%；KNN 分类器SCC-LDA的平均识别率比LDA高出9.15%，比SCC高出6.45%。各类训练样本数为6 和7 时，效果也同样明显。

表3 为分别用MD 分类器和KNN 分类器对Yale_32×32 人脸数据，在各类训练样本数为5、6、7的情况下进行20 次分类，统计出的平均识别率、平均Kappa系数和运行时间。

从表3 中可以看出，两种分类器在各类训练样本数为5、6、7 时，本文所提SCC-LDA 方法的平均识别率，相比SCC 法和LDA 法，均有显著提高，同时识别率标准差最小，Kappa 系数最大；SCC-LDA法的运行时间较LDA 有显著缩短。以各类训练样本数为5 为例，MD 分类器SCC-LDA 平均识别率比LDA 高出9.6%，比SCC 高出16.2%；KNN 分类器SCC-LDA 的平均识别率比LDA 高出15.07%，比SCC 高出19.67%。各类训练样本数为6 和7 时，效果也同样明显。

表4 为分别用MD 分类器和KNN 分类器对Yale_64×64 人脸数据，在各类训练样本数为5、6、7的情况下进行20 次分类，统计出的平均识别率、平均Kappa系数和运行时间。

表3 Yale_32×32数据MD、KNN分类器的识别率Kappa系数和运行时间

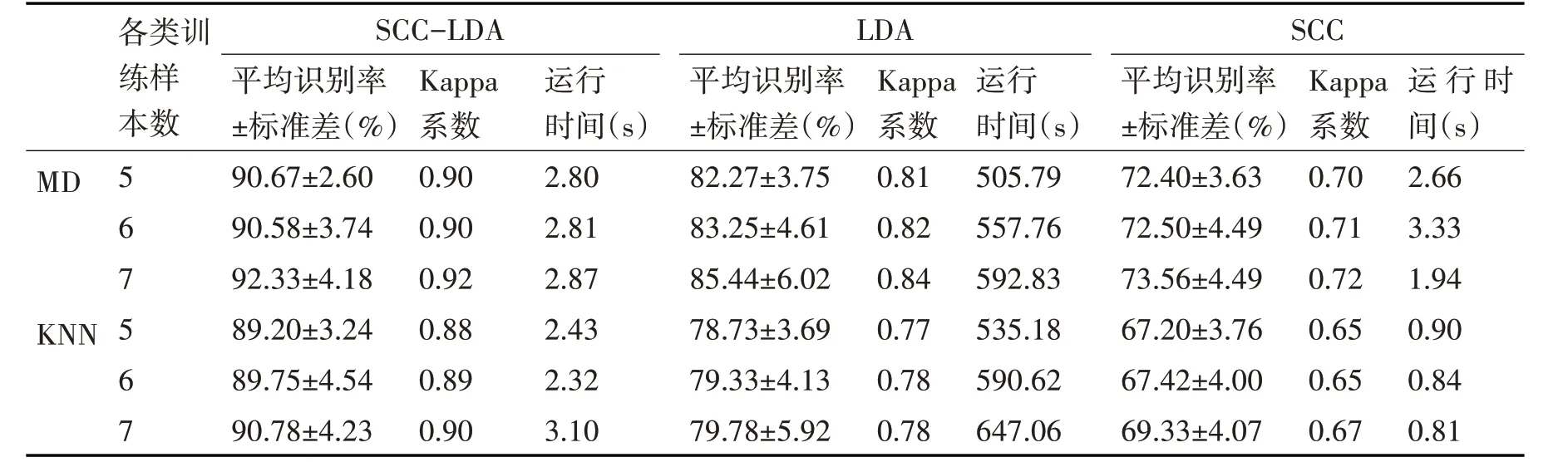
表4 Yale_64×64数据MD、KNN分类器的识别率Kappa系数和运行时间

从表4 中可以看出，两种分类器在各类训练样本数为5、6、7 时，本文所提SCC-LDA 方法的平均识别率，相比SCC 法和LDA 法，均有显著提高，同时识别率标准差最小，Kappa 系数最大；SCC-LDA法的运行时间较LDA 有显著缩短。以各类训练样本数为5 为例，MD 分类器SCC-LDA 平均识别率比LDA 高出8.4%，比SCC 高出18.27%；KNN 分类器SCC-LDA 的平均识别率比LDA 高出10.47%，比SCC 高出22%。各类训练样本数为6 和7 时，效果也同样明显。

5.3 SCC基向量个数对SCC-LDA影响分析

SCC-LDA 中第一步SCC 非监督特征提取所得SCC 基向量的个数，会影响最终SCC-LDA 特征提取的效果。图1 为ORL_32×32 数据采用MD 分类器分别在SCC-LDA 子空间、SCC 子空间、LDA 子空间，20 次分类的平均识别率随SCC 基向量个数变化的对比。LDA法没有用到SCC，所以LDA法的识别率在图中为一条直线，为更好地进行识别率对比将其放入图中。

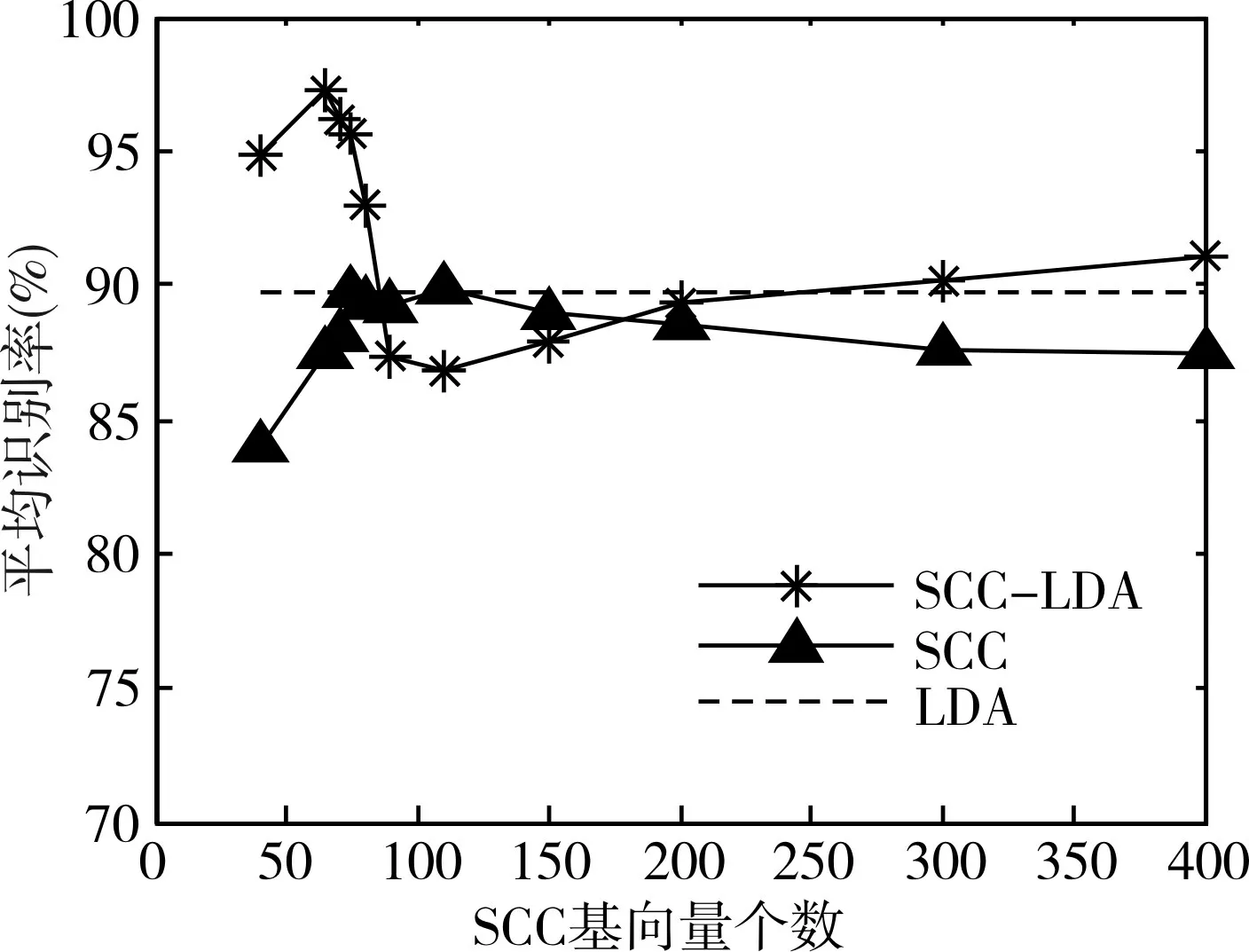
图1 SCC基向量个数对识别率影响曲线图

从图1 可以看出，随着SCC 基向量数的增加，SCC-LDA 识别率存在波动。ORL 数据为40 类，SCC-LDA 在SCC 基向量个数为68 时识别率最高，随着SCC 基向量个数的增加，识别率先快速下降，然后缓慢上升，最终趋于平稳。这是由于，SCC 的基向量是从原始数据中提取出的概念（Concept），概念的个数至少应等于类别数，即每一类至少由一个概念来表达；另一方面，概念并非越多越好，概念过多，反而不利于捕获数据的流形，且不利于稀疏表达。

6 结语

本文提出了一种新的半监督人脸数据特征提取方法——SCC-LDA。SCC-LDA 结合了SCC 和LDA 的优点，采用LDA 对最接近数据流形嵌入的稀疏表达进行特征提取，解决了LDA 不能提取出包含在无类标样本中的可分性信息的问题。ORL和Yale 人脸数据的实验结果表明，相比SCC 和LDA，SCC-LDA 可显著提高人脸识别率，并可加快人脸识别速度。