基于MapReduce 的模糊K-means 算法并行化研究∗

杨延庆 袁华兵

（西安医学院信息技术处 西安 710021）

1 引言

数据挖掘是一种决策支持过程，是指从大量数据中自动搜索出隐藏的具有特殊关系性并存在潜在价值的信息的过程，对科学研究和商业决策起着重要的作用。

聚类分析融合了统计学的思想，能够衡量不同数据源间的相似性，把数据源分类到不同的簇中，是数据挖掘中重要的一个分支。K-means 算法是一种常用的聚类算法，该算法认为簇是由距离靠近的对象组成的，根据数据对象与各个簇中心的距离将其赋给最近的簇。K-means 算法是一种硬聚类算法，该算法定量描述了数据对象间的亲疏关系，数据对象与簇的隶属关系只有0 和1 两个值，即每个数据对象仅属于一个簇。但是，在现实生活中，很多事物间的关系是很难明确的，以天气为例，晴天和阴天的界限是很难分割的。

模糊K-means 算法通过引入模糊理论［1］建立样本对象类属的不确定性描述，能够比较客观地反映现实世界中数据对象的亲疏关系，具有重要的理论与实际应用价值。然而，在数据呈爆炸式增长趋势的今天，从海量数据中进行挖掘，传统的聚类算法逐步暴露出时间、空间等多方面瓶颈。高效地执行计算与海量可扩展存储已迫在眉睫。

MapReduce编程模型［2］是Google提出的利用集群来处理大规模数据集的并行计算框架，Hadoo［3］是Apache基金会开发的一个分布式系统架构，其开源实现了MapReduce 计算模型。Hadoop 通过组织一定规模集群，构建分布式平台对大规模数据进行计算和存储，成为目前主流的云计算技术平台［4～5］。文献［6～8］中，作者基于MapReduce 编程模型，对K-means聚类算法的并行化进行了深入研究，并对并行算法的性能给出了详细的阐述。国内外很多学者都在Hadoop 平台上对其他多种数据挖掘算法进行了并行化研究［9～12］。

本文在基于Hadoop 的分布式计算平台上，研究了模糊K-means 算法的MapReduce 模型并行化实现，并进行了相关试验。

2 模糊K-means聚类［13］

设X={x1,x2,x3,…,xn}是含有n 个对象的待聚类样本集合，其中，每个样本对象xi有t 个属性，xi={xi1,xi2,xi3,…,xit}。将对象样本集和X 划分为K 个簇{c1,c2,c3,…,ck}，设uji为样本对象xi对于第j 簇类的隶属度。K-means 聚类算法中，隶属度函数uji={0,1}，样本对象xi对于某一簇类的隶属度只有0和1，这是一种硬聚类算法，其主要依据是“类内误差平方和最小化”准则。在uji={1} 情况下，xi对第j 个簇类隶属度为1，而对于其他簇类的隶属度全为0，xi与其他簇类间的一些隐藏关系K-means算法无法给出描述。

在模糊K-means 算法中，提出了“类内加权误差平方和最小化”准则［4］，一个对象样本可以属于多个簇类，令uji∈[0,1],i=1,2,…,n,j=1,2,…,k，即给予对象样本xi一个与簇类距离成反比的一个非绝对0，1 的加权隶属函数，且满足任一个样本对象对于各簇类的隶属度之和为1。

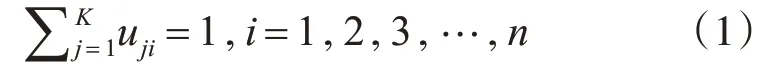
定义目标函数为

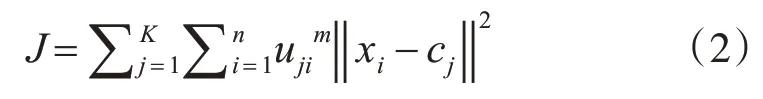
其中，m 为模糊指数，决定了聚类结果的模糊程度，通常取2。

使得目标函数式（2）达到最小值min(J)，根据约束条件式（1），对cj和uji求偏导，得到最优解：

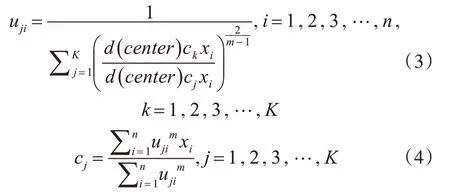
模糊K-means算法的主要步骤如下：

1）初始化簇类中心；

2）初始化对象样本对簇类的隶属值；

3）重复执行以下步骤，直至隶属值收敛或达到迭代次数。

（1）根据式（4），计算新的簇类中心；

（2）根据式（3），计算每个对象样本对于各簇类中心的新的隶属函数值。

3 基于MapRecude的模糊K-means并行算法

3.1 MapReduce模型

MapReduce 采取“分而治之”的编程思想：把大规模的计算任务分解成若干个子任务，各子任务在集群中各分节点分别执行，然后整合各节点的中间结果，得到最终结果。简而言之，MapReduce 就是“任务的分解与结果的汇总”［14～17］。MapReduce 计算过程分为Map（映射）和Reduce（规约）两个阶段，前者负责子任务的执行，得出中间结果，后者负责汇总中间结果。

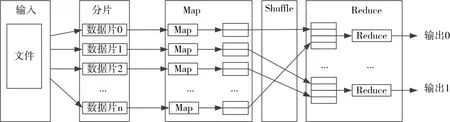
图1 MapRduce运行机制

在输入阶段，一个大的输入文件被划分为若干个较小的文件块；在M 阶段，指派多个Map 并行计算分解后的数据块，得到一系列中间结果；Shuffle阶段，对各节点Map 的输出进行分割重组，以减少带宽的不必要消耗；R 阶段获得重组后的数据，进行相关计算，得到最终结果。图1 描述了MaRduce的运行机制。

3.2 模糊K-means并行算法

模糊K-means 算法的MapReduce 模型并行化实现的基本思路：串行算法的每一次迭代计算，相应地启动一次MapReduce任务，完成对象样本与聚类中心的隶属度计算和新的聚类中心。图2 描述了一次MapReduce任务的算法流程。

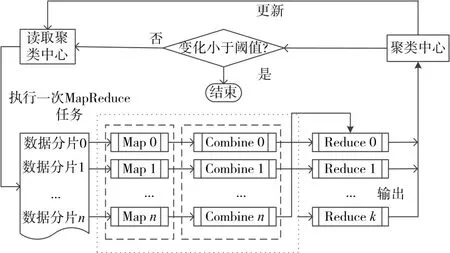
图2 并行化模糊K-means算法的一次MapReduce任务

3.2.1 Map函数任务分析

Map 函数主要是读取被分配的对象样本和上一次迭代过程产生的聚类中心（或第一次初始化的聚类中心），由式（3）和式（4）计算对象样本与各聚类中心的隶属度uji以及用于计算新的聚类中心的临时变量

3.2.2 Combine函数任务分析

Combine 函数相当于一次本地的Reduce 规约操作，Combine 函数的设计思路为：本地节点Map函数的输出传递给其他节点的Reduce 函数之前，对Map 函数输出的相同key 值的隶属度uji和临时变量进行一次“聚类中心预计算”过程，在不影响最终结果的条件下，将具有相同key 值的对合并，可以减小节点间传输开销。

3.2.3 Reduce函数的设计

Reduce 函数的任务是获取多个Map 函数输出的中间结果计算出新的聚类中心，做为下一次MapReduce 任务的输入聚类中心进行后续迭代计算。Reduce函数的伪代码如下：

输入：LongWritable key，Iterator＜LongWritable key，DoubleArray point＞values

输出：Context context

4 实验设计与结果分析

4.1 实验环境与实验数据

实验环境为由8 台主机搭建的Hadoop 分布式集群，包括1 个主节点（NameNode）和7 个从节点（DataNode），主节点控制集群文件系统的命名空间和客户端的访问控制，以及任务分配，从节点负责管理具体作业子任务的执行（包括启动和监控作业、获取其输出，以及通知主节点作业完成）。各节点具有相同的硬件和软件环境配置。硬件配置：处理器：Intel（R）Pentium（R）D CPU 3.00GHz，内存：2.00GHz，硬盘：160G；软件环境配置：操作系统Ubuntu 12.04，Hadoop 版本：hadoop-1.1.1，JDK 版本：JDK1.6.0_30。串行算法单机测试环境具有集群单节点相同的硬件和软件环境配置。

实验中为了考察并行模糊K-means 算法在Hadoop 集群中处理不同规模数据集时的性能，采用Matlab 中的随机函数生成了如表1 所示的五组小规模数据集和表2 所示的两组较大规模数据集，其中每条记录15维。

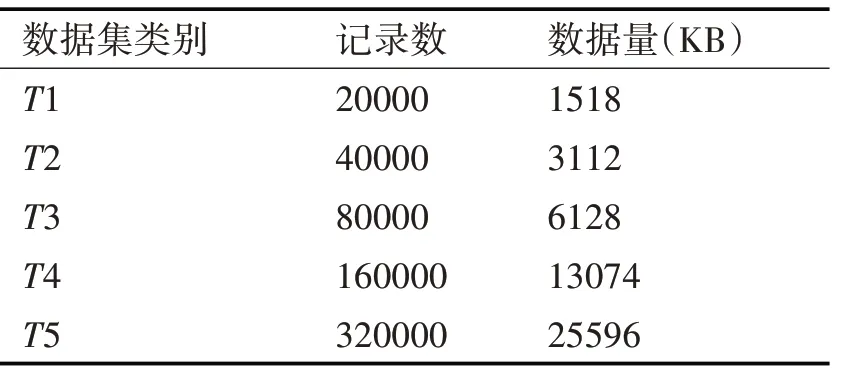
表1 小规模数据集

表2 较大规模数据集

4.2 结果分析

4.2.1 单节点性能比较实验

为了验证模糊K-means 算法在单个节点的集群中并行处理和单机环境中处理同一规模数据集的执行情况，选用数据集为T1，T2，T3，T4，T5，分别测试单机环境完成计算的消耗时间t1 和节点数为1 的集群环境完成计算的消耗时间t2，实验中初始聚类中心随机产生，最大迭代次数设为10，收敛阈值设为0.01。实验结果如表3所示。

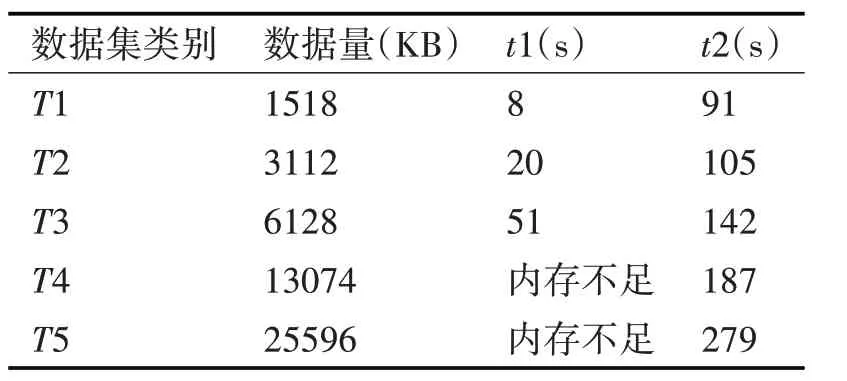
表3 单节点实验结果

实验表明，输入数据集规模很小时，单机串行计算效率远远高于Hadoop 集群节点并行算法，主要原因是Hadoop 集群中用于实际计算的资源只占了总体消耗中很小的一部分，大部分资源被MapReduce 任务的启动和交互所消耗。随着输入数据集规模逐渐增大，单机串行计算就会出现内存不足，计算任务终止，而Hadoop 集群能够顺利完成计算任务，且计算速度未明显降低。这一点体现了基于MapReduce 的并行模糊K-means 算法在Hadoop平台上具有处理大规模数据的能力。

4.2.2 集群加速比性能实验

为了验证集群节点增加时，对相同规模大小的输入数据集，系统的处理能力。选用数据集为T6，T7，分别测试节点数为1，3，5，7 时，集群完成计算所消耗的时间，实验中初始聚类中心随机产生，最大迭代次数设为10，收敛阈值设为0.01。集群处理时间结果如图3所示。

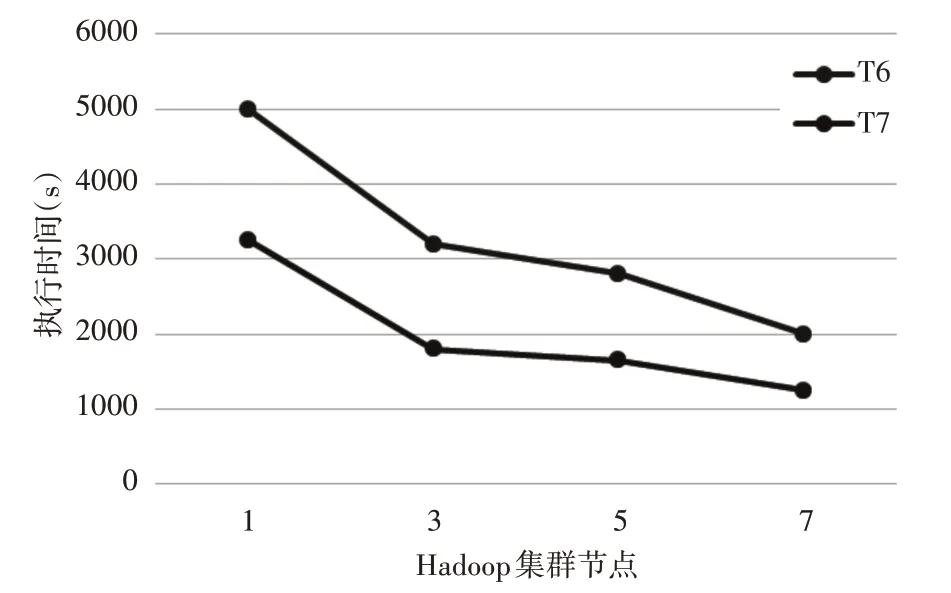
图3 集群多节点处理时间

实验表明，随着节点的增加，Hadoop 集群处理输入数据集T6，T7的执行时间逐渐减少，增加节点可以提高集群处理相同规模数据集的计算能力，并且在相同节点数下，处理数据集规模增加1.6倍时，执行速度提高了约1.9 倍。这说明基于MapReduce的并行模糊K-means 算法在Hadoop 集群中具有良好的加速比。

5 结语

为了提高模糊K-means 算法对大规模数据的聚类能力，本文通过在Hadoop 分布式计算平台上对模糊K-means 算法的MapReduce 并行化进行了研究和实验，实验表明：模糊K-means 算法MapReduce 并行化后，应用在Hadoop 分布式集群中，提高了模糊K-means 算法对大规模数据的处理能力和计算效率，而且具有良好的加速比。