基于轮盘赌反向选择机制的果蝇优化算法∗

张 静 高 尚

（江苏科技大学计算机学院 镇江 212003）

1 引言

果蝇优化算法（Fruit fly optimization algorithm，FOA）是潘文超博士于2011年6月在果蝇觅食行为中得到启发从而提出的。果蝇优化算法是一种全局优化群智能算法［1～2］，该算法用以求解数学函数极值、微调Z-SCORE模型系数、广义回归神经网络参数优化［3～4］、船舶操纵响应模型的辨识与语音信号盲分离［5］等各种领域。由于果蝇优化算法是新兴的智能算法，对其理论研究不够成熟，同时研究成果也不是很多，因此，对果蝇优化算法的相关研究需要积极展开。

果蝇优化算法简单易于理解，程序容易实现，运行所需时间较短，受影响的参数较少，仅有三个：初始位置、种群大小和迭代步长。所以该算法与其他群智能算法相比，具有一定的优势（如遗传算法需要调整5个参数［6］，易早熟收敛且计算量大；粒子群算法需要调整5个参数［7］，易陷入局部最优；蚁群算法需要调整7个参数［8］，过于复杂限制了其应用；免疫算法需要调整5个参数［9］，复杂而且计算量大；人工鱼群算法需要调整5 个参数［10］，计算量大）［11］。果蝇优化算法与其他全局优化算法近似，都是希望通过迭代从而找到全局最优值，但若此最优个体不是全局最优，则极易使得算法陷入局部最优，会导致后期收敛速度缓慢，寻优精度偏低。本文针对基本FOA 算法寻优精度不高，易陷入局部最优的缺点，并从保持种群多样性以提高果蝇优化算法的全局寻优能力的角度出发，在该算法在迭代过程中，采用基于轮盘赌法反向选择机制来选择搜索步长，即果蝇群体中适应度越低的个体食物源被选择的概率越大，这选择策略与轮盘赌选择机制相反，从而避免果蝇整体种群迅速向某些适应度值过高的个体进化，达到保持果蝇种群多样性的目的，最终达到避免果蝇优化算法的过早收敛。

2 果蝇算法

2.1 基本原理

果蝇算法是一种根据果蝇觅食行为推演出寻求全局优化方法。果蝇相比于其他物种具有更好的感官知觉，特别是在气味和视觉方面。果蝇的嗅觉器官能收集到漂浮在周围空气中的各类气味，甚至可以闻到40km 之外的食物。然后，当它飞到食物位置附近后，就可使用敏锐的视觉发现食物和同伴聚集的位置，从而向食物方向飞去［1］。

2.2 算法过程

根据果蝇搜寻食物的过程，我们可以将其总结为以下必要步骤［1］。

Step1 初始化参数：群体规模popsize，最大迭代词数max gen，随机初始化果蝇群体位置X_axis，Y_axis；

Step2 赋予果蝇个体利用嗅觉搜寻食物的随机方向和距离，式（1）中，Random 为搜索距离，其表示一般的随机数：

Step3 由于无法得知食物的具体位置，应先计算与原点之间的距离Disti，再计算味道浓度判断值Si，此值为距离之倒数：

Step4 将味道浓度判断值Si代入味道浓度判断函数（适应度函数），从而求得果蝇个体的味道浓度Smelli：

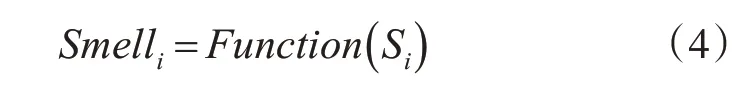
Step5 找出果蝇种群中味道浓度最佳的果蝇（以最小化问题为例）：

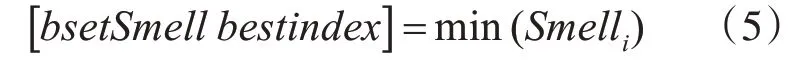
Step6 保留最优味道浓度值以及其对应的X、Y坐标，果蝇群体利用视觉向该位置飞去：

Step7 此时果蝇种群进入迭代寻优。重复执行Step2～Step5，并判断当前味道浓度是否由于历史味道浓度，且当前迭代次数小于最大迭代次数max gen，若是则执行Step6；否则，结束算法。

2.3 果蝇算法的不足

果蝇算法虽然拥有结构简单、参数少、易调节、易于理解和实现，成功地应用于多个方面，但是随着研究的深入，算法还存在收敛速度慢、寻优精度低等缺点，当位置更新时，当前最优个体易于陷入局部极值，并且没有有效的机制来跳出该局部极值，导致种群停止进化，最终出现全局寻优失败，特别是在解决多峰、高维等复杂问题时会陷入局部最优值，导致全局搜索能力较差。

3 改进后的果蝇算法

3.1 轮盘赌策略

传统的轮盘赌策略是使用适应度值与总适应度值的比率作为选择概率［12］，这是一种贪婪的选择方式，这种选择策略使果蝇种群在具有高适应度值得食物中聚集，从而减少了种群的多样性。因此反向轮盘赌的选择策略［13］被引入到果蝇算法中，所谓反向轮盘赌选择策略，就是将传统轮盘赌策略中的概率式（7）：

其中fiti是第i 个解的适应度值，N是解的个数。

换成如下的概率式（8）：

也就是说，适应度值得倒数与总适应度值的倒数之间的比率被用于优化果蝇种群。从公式可以看出，适应度值越大，适应度值的倒数的概率就越小，这就可以保持果蝇种群的多样性，并且不容易陷入局部最优。

3.2 改进后的算法过程

改进后的果蝇优化算法的可归纳为以下几个步骤。

Step1 初始化参数：群体规模popsize，最大迭代词数max gen，随机初始化果蝇群体位置X_axis，Y_axis；

Step2 执行FOA算法的step2～step6；

Step3 根据式（8）确定个果蝇的味道浓度判定值Si的适应值；

Step4 采用反向轮盘赌发策略从Si中确定全局最优的某个替代值(bestX,bestY)作为果蝇的搜索距离，然后根据式（9）更新果蝇的位置：

Step5 根据式（10）计算果蝇原点之间的距离Disti*和式（11）味道浓度判断值Si*：

Step6计算果蝇个体的味道浓度Smelli*：

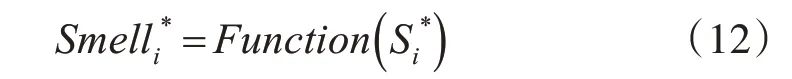
Step7 若Smelli*＜Smellbest，则保留最优味道浓度值以及其对应的X、Y坐标，果蝇群体利用视觉向该位置飞去：

Step8 进入迭代寻优，重复执行Step3～Step7，直至当前迭代次数达到最大迭代次数max gen 或者已经达到理论最优值。

4 数值仿真与分析

4.1 一元函数优化问题

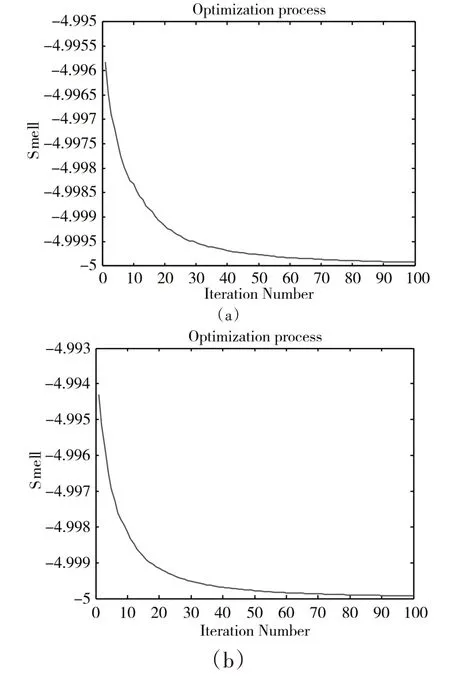
图1 不同种群规模下FOA迭代过程图

一元函数举例函数如下：min f(x)= -5+x2,x∈(-10,10)。

应用传统的FOA 算法得到迭代结果如图1 所示，迭代次数为100，种群规模分别为20和30。

种群规模为20时，迭代到71次达到1e-4精度，种群规模为30 时，迭代到64 次达到1e-4精度。可见增加种群规模对其收敛速度改进不大。

在种群规模、迭代次数相同的条件下，为了更加值观地得到改进后的FOA 算法的寻优效果，图2展示了传统的FOA 算法、改进后的FOA 算法和SA-FOA［14］算法的优化过程。

图2 传统FOA和改进后的FOA比较

由图2 可知，相比于FOA 算法和SA-FOA［14］算法，改进后的FOA 算法经过两次迭代即可达到1e-4精度，收敛速度非常快，步长改进效果明显，且精度较高。

4.2 多元函数优化问题

潘文超教授的相关著作中只提到关于一元二次函数的极值优化应用，这里将本文提出改进后的FOA 算法运用到多元函数求解最优值，与基本的FOA 和SA-FOA［14］算法进行比较。本文从常用于优化算法比较的测试函数中选择四个来进行验证，函数名称、函数表达式和理论最优解如表1 所示，Sphere 函数是单峰函数，其他函数皆为多峰函数。另外，Ackley 的函数搜索非常复杂，这是通过叠加中等放大指数函数的余弦而获得的连续实验函数，其特征在于，通过余弦波调制几乎平坦的区域以形成孔或者峰，从而使表面起伏，并且很难找到最优值，容易陷入局部最优，因此，与其他三个函数相比，该函数寻优难度较大。在进行测试时本文打算从两方面进行：第一，算法的可行性分析，即寻优性能分析，在种群规模和迭代次数相同时，将收敛速度和寻优精度与其他算法进行比较；第二，算法的性能分析，即比较两种算法的迭代次数与运行时间。

4.2.1 寻优性能分析

设定该果蝇种群规模的大小为30，固定迭代次数为100。在本文中，用FOA 算法、SA-FOA［14］算法和改进后的FOA 算法用于对四个测试函数执行20 次独立测试。测试结果如表2 和图3 所示，对于每个测试函数，其平均值反映了在相同种群规模和迭代次数下每种算法所达到的解的精度，标准方差反映了每种算法的鲁棒性和稳定性。

表1 算法测试函数

表2 FOA算法与MFOA算法的性能比较

从表2 可得出，对四个测试函数，相比FOA 算法和SA-FOA［14］算法，本文提出的改进后的FOA 算法都能找到或者更接近于理论最优值，其求解得到的最差值、最优值、平均值和标准方差均优于FOA算法和SA-FOA［14］算法，改进后的FOA对函数f1(x)的寻优精度相比FOA 高出了100多个数量级；改进后的FOA 对函数f2(x)和f3(x)寻优成功率（寻优成功率=找到最优值的运行次数/总的运行次数）能达到100%；对于复杂结构的f4(x)，改进后的FOA的寻优精度也是较高。对比三种算法20 次运行后的平均值和标准方差，可以得出，改进后的FOA 的平均值要远远低于FOA 和SA-FOA［14］算法，更接近或者等于理论最优解；除此之外，改进后的FOA 的方差较低。因此，本文算法搜索最优值的能力更强，解的精度更高，更具有较好的鲁棒性。

图3 显示了的三种算法的优化测试曲线。从图3 中可以看出，在迭代次数为200 时，改进后的FOA 比传统FOA 以及SA-FOA［14］算法的收敛速度都更快（接近最优解时FOA 迭代次数大约100、97、80、110；改进后的FOA 迭代次数大约为7、8、6、12；SA-FOA［14］迭代次数大约为48、48、24、60），并且寻优精度比其他两种算法要高出很多。由图3 中的（a）、（b）和（c）可以得出，三种算法对单峰函数和多峰函数具有较好的寻优效果，但是改进后的FOA算法效果更优；虽然对于结构相对复杂的多峰函数，三种算法都没有达到与另外几个函数一样的寻优结果。然而，改进的FOA 算法寻优精度和收敛速度仍然优于其他两种算法。因此，本文算法能够更好地跳出局部极值，具有更高的收敛精度和更强的寻优性能。

4.2.2 算法性能分析

算法的效率指的是算法的执行时间随问题规模的大小增加而增长的趋势。改进算法是否有效、可行，除了提高寻优性能，其自身的时间复杂度也应该更低。由于任何一个算法都包括控制结构和许多原操作，因此从算法中选择作为所研究问题的基本操作的原始操作在算法中的执行次数为依据。FOA算法中，主要是测试函数的维数影响着算法的时间复杂度。选用以上三个测试函数（f1(x)是单峰函数）对本文算法的时间复杂度进行测试并分析，设置种群规模为30，迭代次数为200，独立运行20 次，计算两种算法在不同维数（200 维数，400维数，600 维数）所需要的平均运行时间，仿真结果如表3所示。

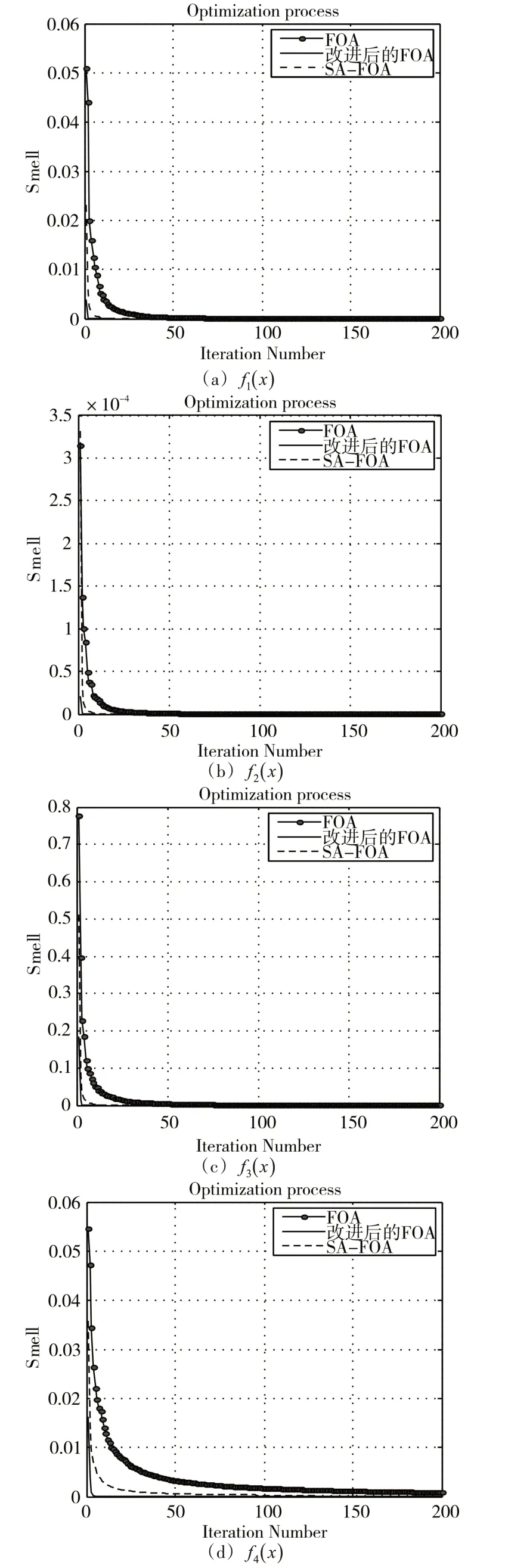
图3 两种算法的优化曲线

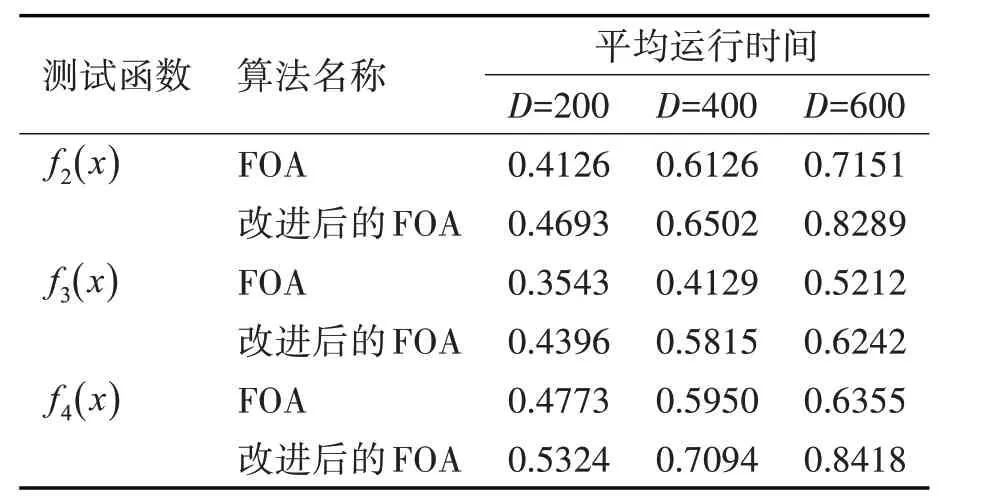
表3 算法平均运行时间对比

从表3 的平均运行时间可以得出结论，改进算法的平均运行时间只比传统的FOA 算法稍长一点，因此本文改进的FOA 算法复杂都较低，是可行有效的。

4.3 与其他算法性能对比

为测试本文算法与其他算法的性能优劣，本文将改进后的FOA 与其他几种算法的优化均值进行了对比，文献中的基于模拟退火的果蝇优化算法［14］（SA-FOA）、文献中的自适应调整参数的果蝇优化算法［15］（FOAAP）、文献自适应混沌果蝇优化算法［16］（ACFOA）和文献中的自适应变异的果蝇优化算法［17］（DDSCFOA），对以上四个测试函数的性能进行比较，迭代次数为2000，种群规模为30，独立运行次数20后取平均值，其运行结果如表4所示。

首先将本文算法比参考文献中的其他算法提高很大，对于函数f1(x)、f2(x)和f3(x)，本文算法能收敛到理论全局最小值；对于函数f4(x)，本文算法平均最优值优于其他算法，最多相差13 个数量级。综上所述，本文算法在实验条件（种群数、迭代次数等）一致的情况下，本文算法的平均优化值要好于参考文献中的算法。因此，与参考文献算法相比，本文算法具有更强的搜索复杂函数的能力，且具有较好的全局搜索能力。

5 结语

果蝇优化算法属于演化式计算的范畴，相比其他群智能算法，FOA算法原理简单，计算速度快，易于实现。本文针对传统果蝇算法寻优精度不高、收敛速度较慢且易于陷入局部最优的特点，提出了基于轮盘赌反向选择机制的果蝇优化算法，通过提高其种群多样性来提高其求解问题时的全局寻优能力。仿真实验表明，与参考文献中的其他果蝇优化算法相比，改进后的FOA 算法在一元函数和多元函数的最优化实例中收敛速度和精度都大大提高，且不易陷入局部最优，可作为求解各类优化问题的实用高效的智能方法，本文算法有效、可行。

表4 MFOA算法与其他算法的性能对比表