基于等级制度和布朗运动的混沌麻雀搜索算法
2021-07-24汤安迪徐登武
汤安迪, 韩 统, 徐登武, 谢 磊
(1.空军工程大学航空工程学院,西安,710038; 2.94855部队,浙江衢州,324000)
群智能优化算法是一类模拟自然界生物行为和自然现象的元启发式优化算法,具有良好的并行性和自主探索性。自1975年美国教授Holland根据达尔文进化论以及自然界优胜劣汰机制提出了遗传算法[1]以后,越来越多的学者通过对不同生物种群和物理现象进行分析,从中获取灵感,提出多种群智能优化算法。包括粒子群算法[2](particle swarm optimization,PSO)、鲸鱼优化算法[3](whale optimization algorithm,WOA)、灰狼优化算法[4](grey wolf optimization,GWO)等。
麻雀搜索算法(sparrow search algorithm,SSA)是薛建凯等[5]于2020年提出的群智能优化算法,具有搜索精度高、收敛快等特点,但其在接近全局最优时,仍旧会出现种群多样性减小、易于陷入局部最优等缺陷。
为了改善群体的多样性,防止算法陷入局部最优,杨万里等[6]利用Logistic映射调整PSO算法惯性权重,通过混沌映射的随机遍历性,使算法在迭代过程中随机选择开发或探索行为;IBRAHIM等[7]利用Logistic映射初始化GWO算法种群,增加初始种群个体多样性,以此增加算法收敛效率;吕鑫等[8]利用Tent映射对SSA算法个体进行扰动,防止算法陷入局部最优。
上述文献主要利用某一种混沌映射对算法进行改进,但没有讨论不同混沌映射对于算法性能改进的影响。本文为解决麻雀搜索算法在迭代后期多样性减弱、易于陷入局部最优的问题,提出利用混沌映射调整麻雀搜索算法关键参数,通过函数测试确定使用哪种混沌映射,并引入GWO算法的等级制度,增强种群多样性,利用布朗运动扩大搜索范围,增强算法探索能力,当算法陷入停滞时,使用布朗运动策略对个体施加扰动,帮助算法跳出局部最优,最后利用贪婪策略有效保留优势个体,加快算法收敛速度。
1 麻雀搜索算法
麻雀搜索算法是一种新兴的群智能优化算法。SSA主要模拟了麻雀觅食的过程。麻雀觅食过程是发现者-跟随者模型的一种,同时还叠加了侦查预警机制。种群中找到食物较好的个体作为发现者,其他个体作为跟随者,同时种群中选取一定比例的个体进行侦查预警,如果发现危险则放弃食物,安全第一。
SSA算法中有发现者、追随者以及警戒者。分别按照各自规则进行位置更新,更新规则如下:
(1)

(2)
式中:Xp表示被发现者占据的最佳位置;Xworst表示当前最差位置,A是一个一行多维的元素为1或-1的矩阵。
(3)
式中:Xbest是当前全局最佳位置;β是步长控制参数;fi是当前麻雀的适应度;fg和fw是当前最佳适应度和最差适应度;ε是一个常数,用于避免分母为零。
2 基于等级制度和布朗运动的混沌麻雀搜索算法
2.1 混沌映射
混沌是一种在非线性动力系统中产生的随机现象,具有规律性、随机性,对初始条件和遍历性敏感。根据这些特征,构造了不同方程表示的混沌图,用以更新优化算法中的随机变量[9]。
在本文中,使用一维且不可逆的混沌映射来生成一组混沌值来改善基本SSA算法的参数,如表1,这10种混沌映射在生成数值时效果不同,且已在文献[10~12]中证明其有效性。

表1 混沌映射
2.2 等级制度策略
麻雀搜索算法在对警戒者更新时,仅考虑当前状态最优解,没有考虑其他次优解,缺少群体间交流,降低种群个体多样性,易使算法陷入局部最优,因此学习灰狼优化算法中的等级制度策略,选取前3个最优解对警戒者进行位置更新,更新公式如下:
(4)

2.3 布朗运动
布朗运动是一个随机过程,其步长取决于一个均值为0、方差为1的高斯分布概率函数,能够更均匀、更可控的步长覆盖搜索空间,布朗运动在点x处的概率密度函数如下:
(5)
麻雀位置更新公式为:
(一)加深学生对于课文的理解激发学生的兴趣。兴趣是最好的老师,要想学生真正的喜欢掌握一门知识,最重要的是让学生对这门课产生极大的兴趣。而具体情境的建设,就可以通过这样的方式让孩子们对语文产生极大的兴趣。并能够更加直观的感受、理解每一篇课文背后的深层含义。
(6)
式中:P=0.5;R为0到1均匀分布的随机数;RB为布朗运动步长。
2.4 改进算法描述
本文针对麻雀搜索算法种群多样性减少、易于陷入局部最优的不足,提出了基于等级制度和布朗运动的混沌麻雀搜索算法(chaos sparrow search algorithm based on hierarchy and Brownian motion,CSSA-HB)。首先利用混沌映射调整麻雀搜索算法的警戒值参数,然后利用等级制度策略和布朗运动策略对种群中优势个体和劣势个体分别进行更新,当算法陷入停滞时,使用布朗运动策略,帮助算法跳出停滞,最后利用贪婪策略保留优势个体,加快算法收敛效率。改进算法流程见图1。
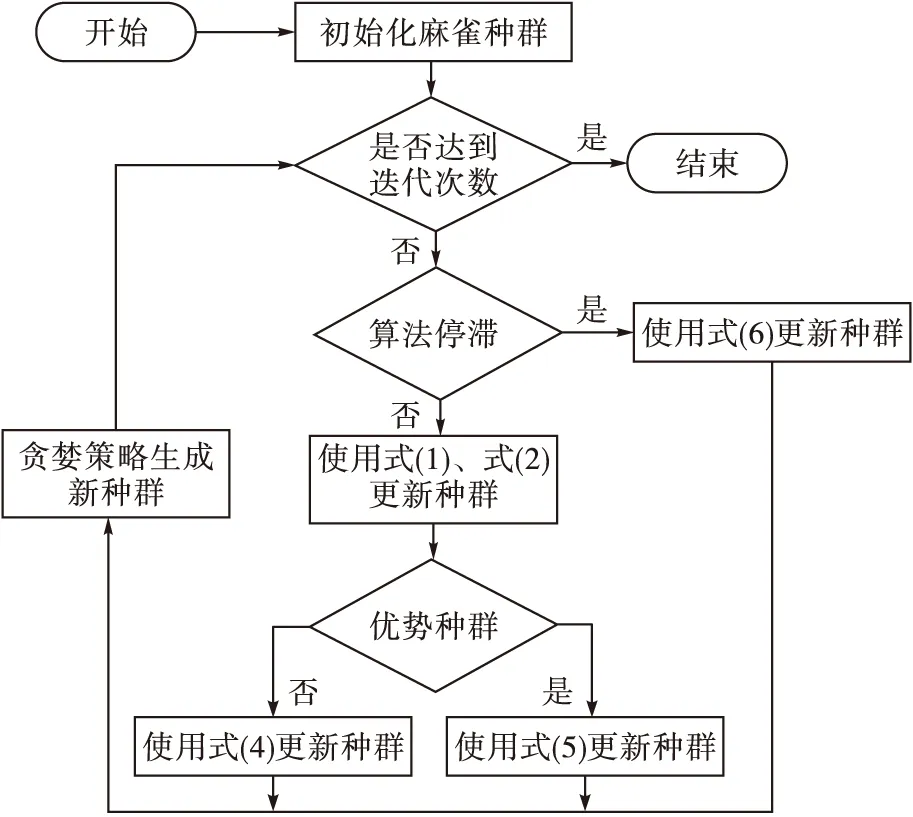
图1 CSSA-HB流程图
3 仿真实验
为确定使用哪种混沌映射调整SSA参数,将SSA与各混沌映射结合,与第1种混沌映射结合的算法命名为SSA-1,与第2种混沌映射结合的算法命名为SSA-2,以此类推,将SSA与上述10种混沌映射分别与SSA结合的算法在12种测试函数中进行比较,测试函数如表2所示。为公平比较,在相同实验平台上,设置种群数为50,最大迭代数为300,算法参数与原文献保持一致。所有算法均使用MATLAB R2018b编程,计算机操作系统为Windows10,处理器为AMD R7 4700 U 16 GB。表3为各算法独立运行30次的统计结果。

表2 测试函数
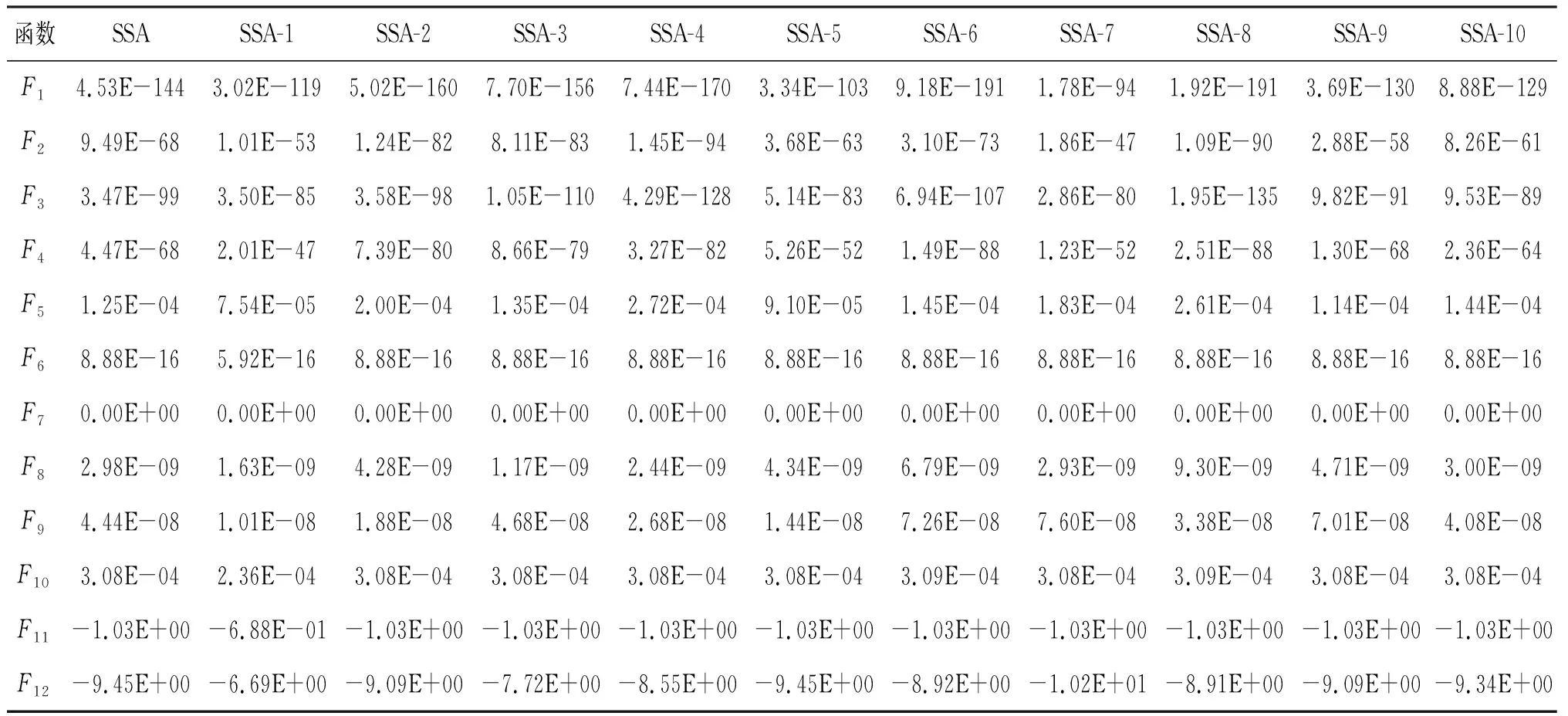
表3 11种混沌映射组合算法计算平均值比较
从表3可以得知,对于F1、F2,有5种映射结合算法优于SSA算法;对于F3、F8,有4种映射结合算法优于SSA算法;对于F4、F9,有6种映射结合算法优于SSA算法;对于F5,有3种映射结合算法优于SSA算法;对于F6、F7、F11,所有算法性能相近;对于F10,则有7种映射结合算法优于SSA算法;而对于F12,仅有2种映射结合算法优于SSA算法。其中,SSA-4算法在7个测试函数中优于原算法,在3个测试函数中与原算法性能差异不大,仅在1个测试函数中表现劣于SSA算法;SSA-3在6个测试函数中优于原算法,在3个测试函数中与原算法性能相近,同样仅在1个测试函数中表现劣于SSA算法。
为了进一步分析混沌映射对于SSA算法的改进能力,根据表3的平均值对各算法进行比较排序,结果如表4所示,最后一栏为各算法平均排序结果。可以得知,其中4种映射结合算法表现优于SSA算法,SSA-4排序第1,寻优性能在11种算法中最强,SSA-3次之,其余算法排名为:SSA-2和SSA-8并列,SSA、SSA-5和SSA-6并列,SSA-10、SSA-9、SSA-1。结合以上分析,混沌映射对于SSA算法的性能具有促进作用,且第4种混沌映射表现最佳,因此在后文对改进算法进行性能测试时,使用该映射进行参数调整。

表4 11种混沌映射组合算法排序结果
为了充分验证CSSA-HB算法的有效性与优越性,选择WOA[3]、GWO[4]、BSO[15]、PSO[14]、FPA[15]以及传统SSA算法进行对比分析,参数同前,表5为各算法独立运行30次的统计结果。最优值加粗体表示。
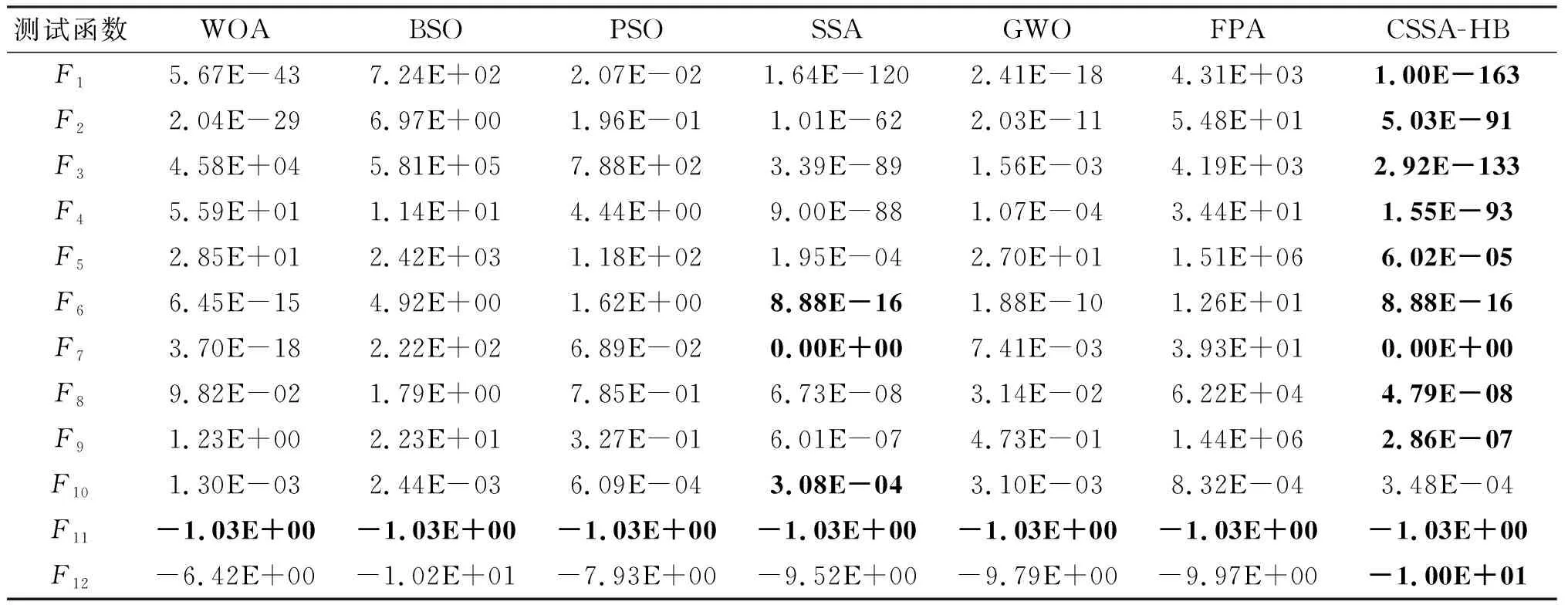
表5 7种算法平均值比较
分析表5可知,对于单峰测试函数F1~F5,CSSA-HB在7种算法中表现最佳,寻优精度和寻优稳定性较其他算法有较大提升,对于多峰测试函数F6~F9,CSSA-HB在F6和F7中表现与原算法相近,但优于其他对比算法,在F8和F9中,CSSA-HB性能优于所有对比算法,对于固定维度测试函数F10~F12,CSSA-HB在F10中寻优效果弱于SSA,但差异不大,在F11中,各算法性能相近,在F12中,CSSA-HB优于所有对比算法。因此,本文提出的CSSA-HB算法在其中8个测试函数中寻优性能最佳,在3个测试函数中与SSA性能相近,优于其余对比算法,仅在1个测试函数中表现差于SSA,证明CSSA-HB算法改进的有效性。
为了进一步验证CSSA-HB算法的寻优性能,根据表5的均值对各算法进行排序,结果如表6所示。
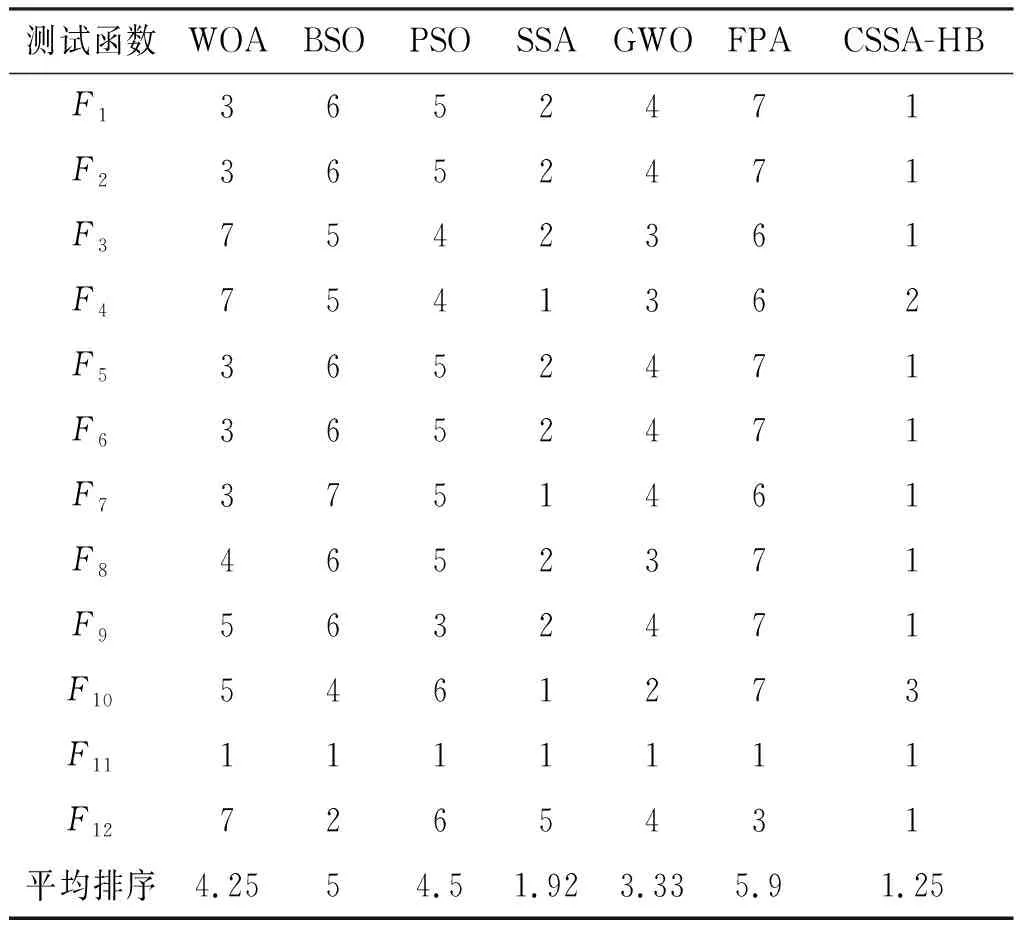
表6 7种算法性能排序结果

图2 7种算法性能雷达图
图3为7种算法独立求解12个基准测试函数30次所得结果的箱式图,从图中可以得知,在进行求解时,CSSA-HB求得的异常点均少于对比算法,且在求解所有测试函数时,收敛值的分布相比其它对比算法整体上更为集中,明显优于其他对比算法,说明改进的CSSA-HB算法具有较强的鲁棒性。
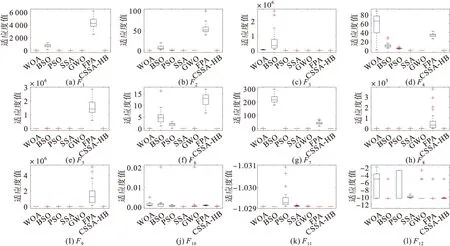
图3 7种算法收敛箱式图
为了进一步阐述CSSA-HB的收敛性能,7种算法独立运行30次求解12个基准测试函数收敛曲线如图4所示。在求解F1~F5、F7、F9和F10时,CSSA-HB有更快的收敛速度和收敛精度,在求解F6和F8时,CSSA-HB收敛速度在前期弱于SSA,但在牺牲一定的收敛速度的情况下,能够在后期更快收敛到全局最优值,且收敛精度优于所有对比算法,在求解F12时,PSO算法性能最佳,但CSSA-HB能在后期收敛到全局最优值。因此CSSA-HB相比SSA,其寻优性能具有明显提升,具有较强局部最优规避能力和更高的收敛精度与收敛速度。

图4 7种算法收敛曲线图
算法运行时间也是衡量算法性能的重要指标,表7列出了各算法求解测试函数的平均计算耗时,由表7可知,CSSA-HB的计算耗时平均排名排在最后,这是由于每一次迭代中都会使用混沌映射,以及在更新警戒者位置时,使用了高斯概率密度函数,同时SSA排在第4,而改进策略的加入进一步加大了计算耗时。另一方面,由前文的收敛性分析可知,相较对比算法,CSSA-HB的收敛速度更快,收敛精度更高,因此增加的计算耗时换来了更好的巡游精度,这是可以接受的。

表7 7种算法计算耗时比较
为进一步体现本文提出的CSSA-HB的有效性,选取几个具有代表的测试函数与文献[8]提出的改进算法在同一条件下进行对比。仿真结果如表8所示。由表8可知,对于单峰测试函数F1和F3,CSSA-HB在平均值和标准差上相较于CSSA至少提升了20个数量级,提升效果明显,对于F2和F4,CSSA-HB至少提升了10个数量级,对于F5,相较于CSSA,CSSA-HB能够更稳定地求解最优值。对于多峰测试函数F6~F12,两种算法各有优劣,对于F7-F9,两种算法性能相似,CSSA-HB在F11上效果好于CSSA,CSSA则在F6、F10、F12上效果更好。总体来说,CSSA-HB在12个测试函数中的9个测试函数上的效果不差于CSSA,表明CSSA-HB的性能更好,再一次验证了本文改进算法的有效性。

表8 CSSA-HB与CSSA算法性能比较
4 结语
本文首先探讨混沌映射调整麻雀搜索算法参数对于麻雀搜索算法性能的影响,然后引入等级制度和布朗运动策略,提出了基于等级制度和布朗运动的混沌麻雀搜索算法,通过12个测试函数验证,结果表明使用迭代映射调整麻雀搜索算法参数效果最佳;利用6个对比算法和改进算法以及原始算法进行比较,证明了本文提出的改进算法寻优性能具有明显提升,具有较强局部最优规避能力和更高的收敛精度与收敛速度。
本文对于麻雀搜索算法的改进主要集中在搜索算子的改进,这些改进策略不仅可以应用于麻雀搜索算法,也可以应用于其他智能优化算法的研究,但改进策略的适用性需进一步验证。同时,机器学习是近些年优化领域的研究热点,可以将麻雀搜索算法与机器学习方法进行结合。此外,随着工业生产需求增大,复杂的现实优化问题对于智能优化算法的要求增多,对于麻雀搜索算法的改进需适应不同问题的特性。尤其是对于实时性要求较高的工程优化问题,需要在算法的精度和速度做更多考虑。
