找准知识生长点 让思维开枝散叶

顾梦瑶

（江苏省无锡市东北塘实验小学 江苏无锡 214191）

《新课程标准》中指出：“数学教学活动必须建立在学生认知发展水平和已有的知识经验基础之上。”这种重视起点教学的观点正体现了“以人为本”的基本教学理念，已为很多的教师所接受。这就意味着小学数学课堂教学应站在儿童立场，准确把握学生的学习起点，把学生的数学知识和生活经验作为教学资源，合理处理教材，调整课堂结构，真正做到以学定教，以教促学。

一、教学导入应关注学生的学习起点

美国教育心理学家奥苏贝尔说过：“影响学习的最重要因素是学生已经知道了什么，要根据学生的原有知识状况进行教学。”数学是一门逻辑性很强的学科，其知识循序渐进，由浅入深。教师要善于抓住新旧知识间的连接点，打破学生思维的阻滞点，使其在获取新知的路上水到渠成。

在新授二年级“1000以内的进位加法”时，教师先出示复习题“131+244，37+58”，让两位学生板演，并要求其余学生快速口算。交流时，教师可提问“在列竖式时要注意什么”。学生归纳，教师板书：1.相同数位对齐；2.从个位算起；3.满十向前一位进一。这种往前移一移的导入方式，在温故中找到了学习基础点，找准了生长点。到了计算千以内的进位加法时，教师可及时利用课堂生成资源，并利用投影仪展示学生的作业（如下），并提问，你有什么想说的？

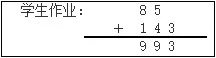
有了复习导入，学生便能利用已有经验，很快发现以上列式中不得当的地方，即相同数位没有对齐。在教师的适当指引下，学生完全明白了“相同数位对齐”的道理，并经历了思维的概括过程。这样既巩固了旧知，又有效掌握了新知。

二、教学过程中，在课堂生成新的学习起点

走进四年级“三角形的分类”一课，在学生初步理解锐角三角形、直角三角形和钝角三角形的特征后，教师要求学生根据信封里露出的一个角来判断其是哪类三角形。教师先露出一个钝角，学生们毫不犹豫地认定这是钝角三角形。接着，教师露出一个直角，学生们齐刷刷地回答是“直角三角形”。学生每猜测完一次，教师就把露出该角的三角形从信封取出，答案当然也在学生的预料之中。两次的“成功”对于学生来说似乎是小菜一碟，更有学生得意地说出“这也太简单了”。最后，教师露出一个锐角，学生们脱口而出“锐角三角形”。然后，一个个瞪大双眼似乎在等待教师把这三角形从信封取出，宣告他们的“成功”。这时，教师向学生们投去质疑的眼光，活跃的课堂一下子安静了下来。一秒，两秒，三秒……终于，有一个声音打破了课堂的沉寂：老师，我不同意！“有何高见？”老师道。学生答：“只有一个锐角还无法判断，因为锐角、直角和钝角三角形中都含有锐角。”一语道破，学生们恍然大悟，纷纷发表自己的见解，认为无法判断，有可能是锐角三角形，也可能是直角三角形，还可能是钝角三角形。待学生们充分交流后，教师便从信封里掏出：一串带有相同锐角的三角形，依次是锐角三角形、直角三角形和钝角三角形。同样大小的一个锐角，通过适时变形，得到三类三角形。教师利用学生“新起点”的差异，引导学生紧扣概念关键，掌握判断时的思考要点，让学生的学习起点顺势上了一个新台阶。

三、教学收尾前，指向可及的学习起点

数学知识环环相扣，一个学习起点的形成将会成为下一次探究新知的基石，从而再次形成新的学习起点，循环往复。课尾，教师可以对教学内容做适当处理，渗透后续知识，为学生补充能量、高筑起点。

（一）为后续学习铺路

例如，在五年级“认识分数”的课尾，教师设计了这样三组题：你能用不同的分数来表示直线上的点吗？

（二）与后续学习接轨

例如，在开展了“小数乘小数”的教学后，教师便安排学生计算“5.2×9和9.8×1.3”。在看似平淡无奇的两个计算题中，有着教师的精心设计，旨在通过复习小数乘整数的乘法，让学生认识到小数与小数相乘和小数与整数相乘的计算方法是一致的，即“因数里一共有几位小数，积就有几位小数，适用于所有的小数乘法”。在此高度概括的基础上，教师再让学生尝试计算“0.28×0.13”。值得称赞的是大多数学生能够紧扣小数乘法的计算方法，根据两个因数中一共有四位小数，而28乘13的积是一个三位数，即364，能够主动在364前写0占位，正确算出0.0364。“在积里点小数点时，位数不够的，要在前面用0补足”，这正是学生下节课要学习的知识点。本练习环节，教师引导学生在复习中温故知新，利用提高题拓展延伸，让学生的学习起点再次实现了质的飞跃。

总之，只有合理掌握学习起点，才能促进知识经验的有效建构；只有敏锐捕捉课堂上生成的“新起点”，才能相互启发，促进知识的高效吸收；只有大胆延生教学内容，尝试接触可及的学习起点，才能拓宽思维，成就高效课堂。