等截面连续箱梁剪力滞效应研究

2020-09-30刘军

山西交通科技 2020年4期

刘军

（山西省交通科技研发有限公司，山西太原 030032）

0 引言

箱梁具有良好的抗弯和抗扭性能，并且结构自重轻，因而被广泛使用和推广。在实际工程中通常采用薄壁箱形梁截面，而薄壁箱梁截面不能采用初等梁理论进行计算。箱梁由于受剪力滞效应影响，其受力状态非常复杂，会造成箱梁翼缘板和腹板交汇处的应力和挠度大大增加，从而发生安全事故[1]。因此对箱梁剪力滞效应的研究至关重要。国内外学者针对剪力滞问题进行一系列的研究，提出了许多计算理论和方法，主要分为弹性理论解法、比拟杆法、能量变分法和数值分析法[2-3]。前3种方法使用范围具有一定的局限性，而数值分析法借助计算机技术可以解决各种力学问题，因此，数值分析法在剪力滞效应分析中具有至关重要的地位[4]。

本文采用数值分析法中的有限元法，借助有限元分析软件研究等截面连续箱梁剪力滞分布特性，为箱梁的设计和施工提供理论基础，具有一定的工程实践价值。

1 剪力滞效应概念

按照初等梁理论，假定离中性轴同一距离的截面，在弯矩作用下，沿宽度方向截面的正应力是相等的。实际上在对称垂直力作用下，翼缘板上的正应力沿宽度方向呈不均匀分布状态。这种由于腹板处剪力流向翼缘板中传递的滞后而导致翼缘板正应力沿宽度方向呈不均匀分布的现象，称为“剪力滞效应”。如果靠近腹板处翼缘板的正应力大于初等梁理论的正应力，称为“正剪力滞效应”，反之称为“负剪力滞效应”。

为了表示剪力滞的影响大小，工程上采用剪力滞系数λσ来表示。剪力滞系数定义为考虑剪力滞效应所求得的正应力与按初等梁理论所求得的正应力的比值。

2 建模分析

2.1 计算模型

模型跨度为5.22 m的两等跨连续直梁，桥型布置图及横截面如图1、图2所示，材料为玻璃钢。计算参数：材料弹性常数E=3 200 MPa，G=1 083 MPa，μ=0.385，不计材料自重。

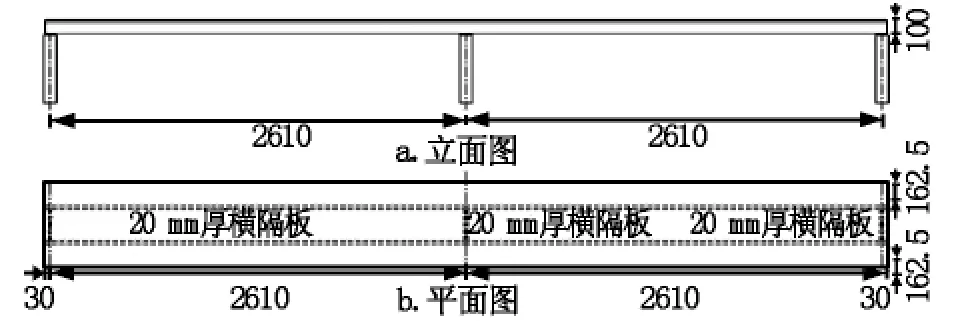
图1 桥型布置图（单位：mm）

图2 连续箱梁横截面构造图（单位：mm）

2.2 计算思路

a）首先利用CAD绘图软件按照所给尺寸绘出截面图形，查询截面特性值。

b）利用有限元软件建立模型，计算出支座反力和截面弯矩，再通过初等梁理论计算出截面上下缘的正应力。

c）通过有限元软件建立计算模型，在考虑剪力滞效应的基础上分析计算模型。

2.3 箱梁截面特性

利用CAD绘制梁横断面图，导入Midas civil界面特性计算器中，计算得到截面惯性矩I=20298599 mm4；中性轴距上翼缘距离y1=33.54 mm；中性轴距下翼缘距离y2=66.46 mm。

2.4 建立有限元模型

利用Midas civil建立两等跨连续梁的计算模型，有限元模型示意图如图3和图4所示，整个有限元模型共11个节点，10个梁单元，建立两种荷载工况，分别施加以下两种荷载：

a）全桥满布均布荷载，荷载集度2.5 kN/m。b）在两跨的跨中同时作用5 kN集中荷载。

图3 Midas模型全图

图4 Midas模型截面图

2.5 按照初等梁理论计算正应力

通过运行分析Midas建立的有限元模型（梁单元），得到相应荷载工况下的梁各支座处的支反力与各控制截面弯矩分别见表1、表2。

表1 两种荷载工况下的支反力 kN

表2 两种荷载工况下的控制截面弯矩 kN·m

根据参考文献 [5]，选取以下22个节点进行比较，节点位置见图5。

以满布均布荷载2.5 kN/m作用时为例，按照初等梁理论截面正应力计算公式计算截面顶底板正应力，计算结果正号表示拉应力，负号表示压应力：

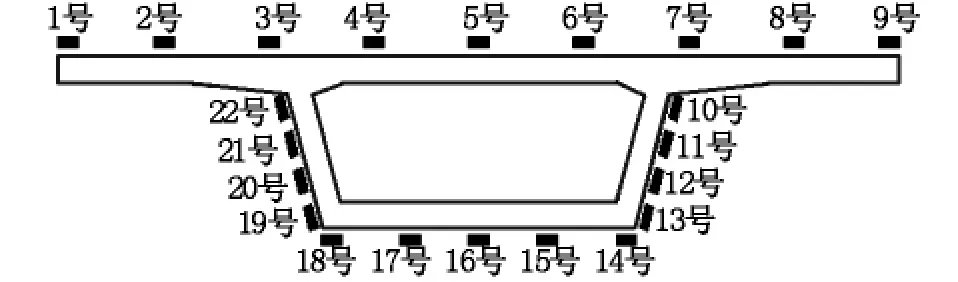
图5 验算节点位置

两种荷载工况下的6个主要位置应力值见表3。其余截面位置处应力根据式（2）～式（7）可计算得到，也可通过线性插值得到。

表3 主要位置应力 MPa

2.6 建立有限元模型

有限元结构模型如图6所示。考虑到剪力滞效应发生在上下翼缘板，以及输出结果的方便性和结果的典型性，在计算精度和模型计算效率的综合考虑下，横截面网格划分情况如图7所示。

图6 计算模型

图7 有限元模型横截面网格划分

2.7 模型边界条件的施加

本模型为两跨连续梁，拟取中间支座为固定支座，顺桥向右侧为横向支座，见图8。有限元模型中通过约束支座处关键的位移来模拟支座，此方式与实际桥梁受力方式相似，但是在约束关键点处会出现应力集中，而实际桥梁中则没有，此处计算结果没有参考价值，故在后续分析中不予说明。

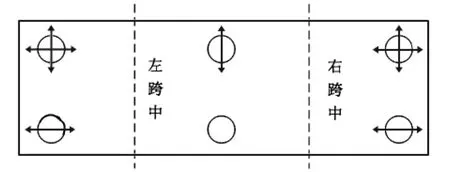
图8 全桥支座布置情况

3 箱梁剪力滞效应研究

3.1 荷载形式对箱梁剪力滞效应的影响

为了研究不同荷载形式对箱梁剪力滞效应的影响，分别在连续梁左、右跨中施加5 kN集中力荷载和施加2.5 kN/m均布荷载，其他参数保持不变。通过初等梁理论以及ANSYS有限元软件计算出结果，提取出跨中和支点截面处截面上、下翼缘节点的正应力数据，计算剪力滞系数，将其绘制成图像，如图9、图10所示。

图9 不同荷载形式截面顶板剪力滞系数变化曲线

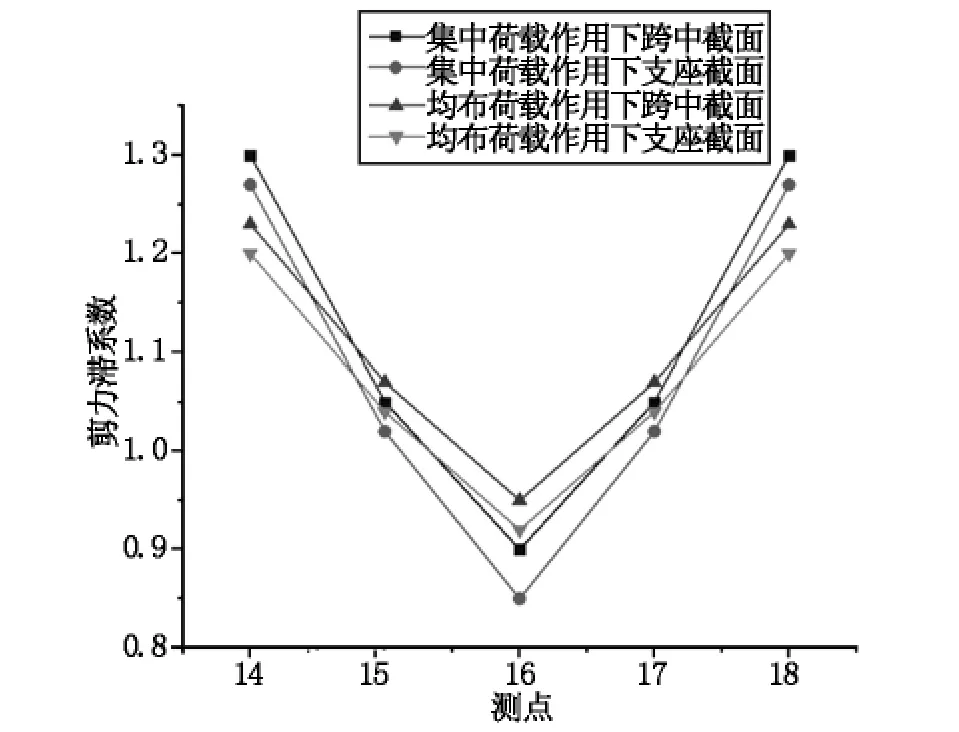
图10 不同荷载形式截面底板剪力滞系数变化曲线

从图9可以看出在不同荷载形式下，跨中和支座截面的顶板均存在明显的正剪力滞效应，顶板测点1～9在不同荷载作用下的剪力滞曲线大致呈M形。在集中荷载作用下跨中和支座截面顶板的剪力滞系数峰值分别为1.41和1.36，而在均布荷载作用下跨中和支座截面顶板的剪力滞系数峰值为1.31和1.26。在集中荷载作用下，跨中和支座截面顶板的剪力滞系数峰值较均布荷载作用时大；在相同荷载作用下，箱梁跨中截面顶板的剪力滞系数峰值大于支座截面顶板的剪力滞系数峰值。

从图10可以看出在不同荷载形式下，跨中和支座截面的底板均存在明显的正剪力滞效应，底板测点14～18在不同荷载作用下的剪力滞曲线大致呈V形。在集中荷载作用下跨中和支座截面底板的剪力滞系数峰值分别为1.31和1.28，而在均布荷载作用下跨中和支座截面底板的剪力滞系数峰值为1.24和1.21。在集中荷载作用下，跨中和支座截面底板的剪力滞系数峰值较均布荷载作用时大；在相同荷载作用下，箱梁跨中截面底板的剪力滞系数峰值大于支座截面底板的剪力滞系数峰值。

3.2 宽跨比和宽高比对箱梁剪力滞效应的影响

为了研究宽跨比对箱梁剪力滞效应的影响和变化规律，保持桥面宽度0.6 m不变，分别将箱梁跨径改为1 m、2 m、3 m、4 m，宽跨比分别为0.15、0.2、0.3、0.6，其他参数保持不变。通过初等梁理论以及ANSYS有限元软件计算出结果，提取出跨中横截面处横截面上翼缘节点的正应力数据，计算剪力滞系数，将其绘制成图像，如图11所示。

为了研究宽高比对箱梁剪力滞效应的影响和变化规律，保持桥面宽度0.6 m不变，分别将箱梁高度改为0.3 m、0.25 m、0.2 m、0.15 m，宽跨比分别为2、2.4、3、4，其他参数保持不变。通过初等梁理论以及ANSYS有限元模型计算出结果，提取出跨中横截面处横截面中上翼缘节点的正应力数据，计算剪力滞系数，将其绘制成图像，如图12所示。

图11 不同宽跨比下左跨中截面顶板剪力滞系数变化曲线

从图11可以看出在不同宽跨比下，左跨中截面顶板的剪力滞系数在腹板位置达到最大值，离腹板越远处剪力滞系数越小，存在明显的正剪力滞效应，同时宽跨比b/l对剪力滞系数的影响非常显著。当宽跨比从0.15增加到0.6时，左跨中截面顶板剪力滞系数峰值从1.11增加到1.60，变化幅度非常显著，而其他测点增幅不明显。随着宽跨比的增加，剪力滞效应逐渐增大。