基于有限元仿真分析的石方路段波形梁护栏性能研究

徐庆峰

（山西省交通新技术发展有限公司，山西 太原 030012）

0 引言

防撞护栏是公路上常见的交通安全防护设施，护栏具有阻挡碰撞车辆穿越、翻越、骑跨的阻挡功能；能够有效降低对碰撞车辆和车内乘员损害程度的缓冲功能；能够使碰撞车辆向行车方向顺利导出并恢复运行状态的导向功能。另外，护栏还具有一定的视线诱导功能。波形梁护栏是一种常用的护栏，其有着维修方便，结构整齐，能够缓解视觉疲劳等诸多优点，且波形梁护栏结构简单，造价及安装费用相对低廉，因此现阶段波形梁护栏在我国各等级公路中广泛使用[1-2]。

石方路基在我国道路施工中较为常见，在遇到石方路基、硬化路肩波形梁护栏立柱不能采用打桩机直接打入段落，目前常用的两种施工方案是：钻孔打入法和混凝土基础法。钻孔打入法是先通过空压钻孔机成孔、回填夯实，再用液压打桩机进行立柱打入；混凝土基础法是先按设计进行基坑开挖、绑扎钢筋，然后进行立柱定位，最后浇筑混凝土、养生。相比较而言，钻孔打入法较混凝土基础法更简捷，施工效率高，工程造价更低。但国内对这两种形式的波形梁护栏的防撞性能对比研究鲜有论著。本文拟通过ANSYS有限元软件模拟车辆撞击试验，重点就这两种形式的波形梁护栏受到车辆撞击时性能进行研究对比，为石方段护栏施工方案的选择提供一定的参考。

1 石方段波形梁护栏形式简介

波形梁护栏是一种半刚性护栏，常见的是两波和三波。这两种护栏也分别有着各自使用的场景，半刚性护栏按照防撞性能分为5个级别，分别是：B、A、SB、SA、SS，根据现行《公路交通安全设施设计规范》波形梁护栏按照表1进行形式选用[3-4]。由于A级波形梁护栏应用最为广泛，因此本文选取A级波形梁护栏作为研究对象。

表1 路基护栏防护等级的选取

现行《公路交通安全设施设计细则》中A级波形梁钢护栏主要推荐如图1、图2所示两种结构形式，即打入式和混凝土基础预埋式。两种结构形式的波形梁护栏上部结构相同，均由（506×85×3）mm圆弧形等截面三波形梁板、三波型防阻块、柱帽和紧固件等组成，所有基底金属材质为碳素结构钢。两种结构的主要区别在于下部，打入式立柱采用Φ140×4.5×2 350 mm钢管立柱，打入道路结构层1 400 mm，外露950 mm；混凝土基础预埋式立柱采用Φ140×4.5×1 450 mm钢管立柱，下设600 mm×600 mm×500 mm混凝土基础，钢管立柱埋入基础400 mm，基础埋入道路结构层100 mm，外露950 mm。

图1 钻孔打入法（Gr-A-4E）

图2 混凝土基础法（Gr-A-4C）

2 仿真模型构建

2.1 碰撞计算数学模型

2.1.1 基本假定

车辆碰撞护栏是十分复杂的过程，到目前为止尚没用精确计算方法来进行描述[5]。为模拟车辆碰撞护栏，本文基于以下基本假设建立数学模型：

a）从车辆碰撞护栏到车辆改变方向平行于护栏停止。

b）车辆的竖向加速度和转动加速度忽略不计。

c）车辆改变方向平行于护栏时车辆的横向速度分量为0。

d）车辆在改变方向时不发生绊阻。

e）车辆碰撞护栏期间容许车辆发生变形，但车辆的中心位置不变。

f）车辆近似为质点运动。

g）车辆与护栏、车轮与路面的摩擦力忽略不计。

h）护栏连续设置。

2.1.2 碰撞力学模型求解方程

对于碰撞的大变形非线性问题，通常采用有限元方法对其进行数值求解。本文采用ANSYS软件中的Explicit Dynamics模块进行显式动力学求解，该模块是一个非线性显式有限元程序，其算法基于以下方程：

a）质量守恒方程：

b）能量守恒方程：

c）能量守恒方程：

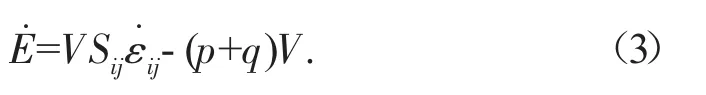
d）控制方程：

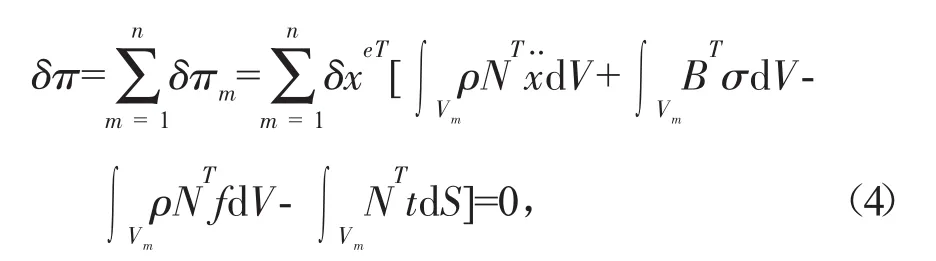
式中：σi，j为柯西应力；f为单位质量体积力；x为加速度；ρ为当前质量密度；ρ0为初始质量密度；J为体积变化率；E为当前构型的体积；εi,j为应变率张量；Si,j为偏应力张量；p、q为碰撞力。

e）汽车护栏碰撞总体方程为：

式中：M为总体质量矩阵；P为总体载荷矢量；Q为等效节点力适量组集；C为节点阻尼阵。

根据式（1）～式（5）及有限元理论，采用Explicit Dynamics模块即可对汽车与波形防护栏碰撞问题进行仿真分析。

2.2 实车碰撞模型构建

2.2.1 模型建立

根据JTG B05-01—2013《公路护栏安全性能评价标准》中的相关要求并以小型客车为碰撞车型建模，主要参数为：碰撞角度为20°，车辆质量为1500kg，车辆行驶速度为100 km/h[6]。综合以上条件、参数建立碰撞模型如图3所示。

图3 护栏模型

2.2.2 材料参数

将碰撞车辆设定为刚体，模型中其他组件按表2设置材料参数。

表2 材料参数表

2.2.3 边界条件

钻孔打入法将立柱下部1 400 mm与道路结构层相连接，道路结构层四周与底面采用固定约束；混凝土基础法将整个混凝土基座600 mm×600 mm×500 mm除外露的表面外与底面结构层相连接，道路结构层四周与地面采用固定约束。汽车重心距地面580 mm，与波形梁护栏20°角度，速度为100 km/h撞向护栏，时间为0.4 s。

2.2.4 网格划分

本次计算由于波形梁护栏结构较为复杂，因此采用弯曲类型的网格对其进行划分，最小网格尺寸为5 mm，最大网格尺寸为20 mm，划分网格后其生成节点84 836个，生成元素220 736个。检查网格质量，格宽高比，网格雅可比，网格扭去系数，网格平行偏差都在较好的范围内，说明网格划分较好，可以采用。

3 仿真结果分析

将模型提交Explicit Dynamics求解器求解，求解完成后处理并提取最大横向动态变形值、等效应力、等效应变等相关参数进行分析。

图4 护栏最大横向动态变形值云图

图4为两种形式的护栏碰撞时的最大横向动态变形值，其表征的是护栏变形后迎撞面相对于其初始位置的最大横向水平位移，该指标可以很好地表征护栏的阻挡功能，其值越小表明护栏的阻挡功能越优越。

图5 护栏最大横向动态变形值-时间曲线

图5将两种形式护栏碰撞过程中的最大横向动态变形值提取并绘制曲线。从曲线来看，碰撞过程中护栏的最大横向动态变形值从0.1 s开始逐渐增大，在约0.3 s时接近最大值，之后略有回弹，然后趋于稳定。总体最大横向动态变形值不超过400 mm，符合《公路护栏安全性能评价标准》中的规定，说明两种形式护栏的阻挡性能都满足要求。在碰撞过程中钻孔打入法形式护栏的最大横向动态变形值始终小于混凝土基础法形式护栏的最大横向动态变形值，表明在阻挡性能方面钻孔打入法护栏优于混凝土基础法护栏。

图6 等效应力

同样将仿真结果中两种护栏的等效应力、等效应变提取出来得到如图6、图7所示曲线。可以发现，碰撞过程中护栏的等效应力和应变都是逐渐增大，在约0.3 s时接近最大值，与横向最大变形量同时达到峰值，然后随着车辆的驶离，数值快速下降。在碰撞过程中钻孔打入法形式护栏的等效应力、等效应变都始终小于混凝土基础法形式护栏的相应指标，表明在力学性能方面钻孔打入法护栏要优于混凝土基础法护栏。

图7 等效应变

将两种形式护栏的最大横向动态变形值、等效应力、等效应变指标的峰值整理汇总得到表3。

表3 分析结果对比表

通过计算可以发现，钻孔打入法护栏的最大横向动态变形值要比混凝土基础法的小80.2 mm，仅为混凝土基础法的79.76%。钻孔打入法护栏的等效应力比混凝土基础法的小130.78 MPa，仅为混凝土基础法的76.40%。钻孔打入法护栏的等效应变比混凝土基础法的小0.778 mm，仅为混凝土基础法的79.69%。综合上述数据表明相比较于混凝土基础法，由于钻孔打入法立柱埋置深度大，更易与道路结构形成整体受力体系，所以能将所受碰撞力更好地扩散，从而降低自身的横向变形、等效应力、等效应变。

4 结论

通过对钻孔打入法和混凝土基础法两种护栏车辆碰撞的有限元模拟可以发现，在相同条件下，钻孔打入法的阻挡性能、力学性能都优于混凝土基础法，并且在实际工程施工中，钻孔打入法较混凝土基础埋入法更简捷，无需养护，施工效率高，也可避免因基坑开挖、混凝土作业对路面造成污染等问题。另外，钻孔打入法相比较于混凝土基础法还具有价格优势。因此，综合使用性能、造价、施工效率等多方面因素，石方路段波形梁护栏推荐采用钻孔打入法。