双模式交通网络中考虑出行者停车行为的集计仿真分析

乔文磊，纪翔峰

(青岛大学商学院，青岛266071)

随着经济的快速发展，当今社会机动车保有量持续增加，以中国为例，截至2019年底，全国汽车保有量达3.48亿辆，与2018年相比，增长了8.83%。机动车保有量的不断增加导致拥堵成为城市交通难以避免的问题，也是学者广泛关注的问题[1]。面对严重的交通拥堵问题，单纯的依靠增加交通供给的方式已经不能够完全缓解拥堵，并且增加交通供给需要大量的交通基础设施建设资金的投入。因此，各个国家从增加交通供给转移到采用高新技术来管理交通系统，从而提高交通网络的通行能力和服务水平。其中，比较典型的代表有交通需求管理[2]。在城市中，特别是大型城市，早晚高峰期间的停车问题对城市的经济、环境以及可持续发展方面都存在重要影响。大量的实证研究表明，在城市交通高峰时间内，未能快速的实现停车所导致的额外交通量能够达到30%，甚至更多，这称之为巡游停车问题[3]。巡游停车问题的出现，导致了交通拥堵问题更为突出。停车政策是当代交通需求管理政策的重要组成部分，例如停车收费，已成为缓解城市交通拥堵的重要举措。通过制定合适的收费策略有助于提高城市交通出行效率，通过调节停车收费策略来进一步影响停车供给与需求之间的关系，使城市交通和通勤者出行和谐发展。除此之外，大力发展公共交通也是缓解城市交通拥堵的另一重要举措[4]，也是交通需求管理重要的组成部分。随着城市的扩张和汽车保有量的持续增加，交通系统也表现出规模大，复杂性高的特点。交通拥堵也不再是分散的小规模交通问题，成为区域性问题，因此治理交通拥堵问题，需要在区域路网层面上进行动态的交通状态监控和交通管理。而对路网进行有效控制和管理的前提，则是路网交通流特性的研究。针对路网交通流特性，宏观基本图理论具有一定的优势，这是本文研究的出发点。宏观基本图的概念是由Daganzo[5]正式提出的，反映了整个路网系统的交通量和路网运行水平之间的关系。城市停车一直是城市交通问题研究的热点，而宏观基本图良好特性对指导现实交通系统的合理控制管理，减少城市拥堵，实现社会停车资源的有效配置，提高停车系统的效率，降低出行成本等有着重要意义。因此自从宏观基本图的概念被提出后，学者们对此进行了大量的研究[6-8]。Zheng[9]考虑了一个具有多种交通方式共享和有限道路空间竞争的复合系统，采用宏观基本图来描述多模型运输系统的交通动态，量化了道路空间分布对拥挤多模式交通系统性能的影响，提出优化乘客总旅行时间定价策略。Liu等[10]针对早高峰通勤问题，通过宏观基本图建立了拥挤市区路网中的通勤均衡模型，设计动态定价模型以降低社会总成本。Amirgholy等[11]将动态拥挤的Vickrey模型与宏观基本图相结合，提出了Bathtub模型。该模型可以通过数值求解来估计通勤问题的精确解，为定价策略提供了参考。Jakob[12]等提出了一个动态的宏观停车收费模型，目标是最大限度地提高收入，最大限度地减少路网上小汽车的巡游时间，该模型对数据的要求较低。Fournier等[13]提出了一个连续近似模型，为停车场的位置和定价的设定，以及所需的周边城市道路的行人通行能力的设定提供参考。本文在已有研究的基础上，基于宏观基本图理论，考虑公共交通和停车的耦合关系，结合小汽车出行者的巡游停车行为，构建城市交通系统的仿真分析模型，重点分析了出行时间和出行成本这两个影响出行者选择的因素；分析了停车收费和公交票价之间的相互影响，揭示其影响机理。

1 模型开发

1.1 仿真区域分析

本文考虑如图1 所示的城市交通系统，包括两个不同的区域，分别是中心区(区域1)和外围区(区域2)两个部分。同时，本文考虑一个双模式城市交通系统，系统中的出行者有两种不同的交通方式可以选择，分别是小汽车和公共交通。除此之外，假设中心区存在公交专用道，而外围区小汽车和公交车混行。因此，本文共存在三个宏观基本图模型，一个应用于外围区，一个应用于中心区的小汽车，一个应用于中心区的公交车。

1.2 系统状态变量演化分析

本节分析与两种不同出行方式相关的系统状态变量的演化，演化的基础由Zheng等[14]的模型演变而来。选择小汽车的出行者(用c 表示)的状态变量演化模型如下所示，表示为离散的形式。其中N 表示区域内交通流的累积量，Q 表示需求，O 表示流出量。式(1)描述了从区域1出发，到达区域1的交通累积量的改变，也就是内部交通量，等于进入区域1的需求和从区域2到达区域1的交通量的总和减去到达区域1的交通量。也可以给予式(2)、(3)、(4)类似的解释。

1.3 停车分析

本文的仿真仅考虑路内停车设施的存在，这也是现实情况中较为常见的形式。为了估计小汽车的巡游时间，考虑三种不同形式的流量[15]:(1)车辆驶向区域内目的地，但还未开始巡游停车，表示为Nr，i(t) ；(2)车辆到达目的地，开始巡游停车，表示为N s，i(t) ；(3)车辆驶向外部目的地区域N o，i(t) ，得

所有路内设施的停车容量为A i，在t时刻使用中的数量为N i(t) 。因此，得到可使用的停车位的数量为A i－N i(t) 。对于第二类车辆，巡游停车表示为如下的重复伯努利试验过程，表示为几何分布。巡游行为直至可用的停车位被找到为止。采用φi(t) 表示车辆到达时停车位可用的概率，其等价于可用停车位和总的停车位的比率，也就是

本文假设只有中心区的停车位是有限的，所以对于外围区域，不存在巡游停车的问题。有关停车的系统状态变量的演化可写为

1.4 集计的模式选择

为了决定新生成交通需求的方式选择，也就是选择小汽车还是公交车，本文采用多项Logit模型来进行方式划分，假设出行者依据最新的出行负效用进行选择。表示选择小汽车的负效用，表示选择公交车的负效用。对于小汽车来说，负效用包括了出行时间，巡游延误和路内停车费用；对于公交车来说，负效用包括了出行时间和公交票价。并且本文假设出行者在出行开始时决定自己的方式选择。因此，本文中出行者选择公交车的比例为

2 仿真分析

假设中心区和外围区都能产生出行需求，中心区产生的需求80%的目的地仍然是中心区，而20%的目的地是外围区；而外围区产生的需求60%的目的地是中心区，余下的40%的目的地是外围区。仿真时间为3个小时，从早上的6点30分到9点30分，共划分成60个仿真时段。其中7点30分到8点30分为高峰时段。各个时段的需求率如表1所示。

假设公交票价为3元，停车费用为10元(不依赖于时间，按次收费)，本文称之为基准情况。多项Logit中的参数αb ＝αc ＝0.5。平均旅行距离1500米。在本文中，采用宏观基本图模型

本文研究的重点是票价的改变对停车的影响，以及停车费用的改变对公共交通的影响。改变公交票价，以及改变停车费用的仿真结果如图2所示，可知，公交票价的升高会导致巡游延误的升高，而停车费用的降低会带来巡游延误的降低。说明本文所提出的模型能够良好的反映现实情况，能够为费用的最优设计提供一定的参考。

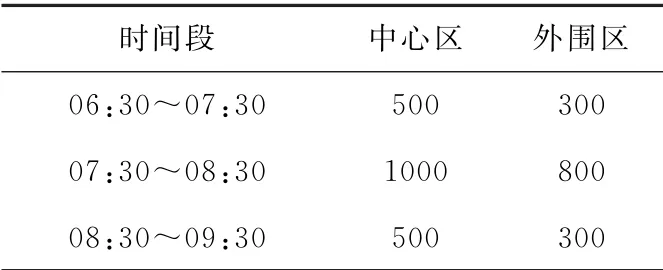
表1 不同时段的交通需求率

3 结论

本文重点考虑了城市交通的早晚高峰期间出行者在到达目的地之前的巡游停车行为，基于宏观基本图理论，基于公共交通和停车的耦合关系构建城市交通系统的仿真分析模型。在该模型中，出行时间和出行成本这两个影响出行者选择行为的因素被刻画。基于模型的仿真结果，分析了停车收费和公交票价之间的相互影响，揭示了影响机理。停车场的定价和公交票价都是给定，未来将探讨如何进行最优设计，现有的研究结果能够为该最优设计提供一定的参考。本文的研究仅考虑了两个区域的简单城市交通网络，没有出行者路径选择行为的影响，在未来的研究中将考虑这一因素。