基于L-M 算法优化BP 神经网络的上市公司信用风险评估研究

仵晓溪，李云飞

(西华师范大学数学与信息学院，四川 南充637009)

随着近年来我国证券市场的快速发展，市场是否规范化、资源配置是否合理化、信息是否对称化等问题逐渐涌现，这不仅会对投资者的利益造成影响，还会有损我国金融市场的正常运行，因而针对上市公司进行信用风险评估，获得财务预警就显得尤为重要。

为解决该问题，国内外学者纷纷对上市公司的信用风险评估展开深入研究。 最初，该研究基本停留在简单的定性分析阶段，主要运用传统的信用分析方法进行评估，比如5C法、LAPP 法以及五级分类法等，这些评价方法虽比较简单，但主观性太强。 于是越来越多的学者逐渐选择多元统计分析方法对此展开研究，较为典型的就是Logistic 模型，这一类方法具有科学实用和客观性等特点，但它要求评价指标满足非多重共线性，恰好与上市公司的财务指标存在高度相关性不符，所以对计算结果的精确性有一定影响。 随着计算机技术的日渐成熟，人工智能方法顺势而生，越来越多的学者将人工智能领域中的机器学习算法引入到企业的信用风险评估研究中。 Odom 和Sharda 最早使用神经网络模型预测企业信用风险情况，他们使用5 个财务指标作为解释变量构建神经网络模型，结果表明该模型的正判率明显优于多元判别分析方法；Tam 和Kiang 还将人工神经网络模型运用于银行破产的研究中，为了提高模型预测的准确性，他们对神经网络学习过程的权值进行了修改，效果十分显著；此外，Boritz、Chris Charalambous 等众多学者在前人的研究基础上，又不断完善、深化了人工神经网络在信用风险评估方向的运用研究。 近年来，人工神经网络也深受国内学者的青睐，杨保安等人针对统计方法中判别分析方法在企业信用风险评估研究中存在的问题，提出了神经网络在该研究方向的优势与潜力；吴德胜等人通过研究不同模型在衡量企业风险情况中的实际使用效果，构建了符合我国企业财务状况的评价指标体系，同时验证了BP 神经网络的可行性和有效性；何欣等人将径向基神经网络和BP 神经网络模型分别应用于中小上市公司信用风险研究，对比结果发现BP 神经网络相较于径向基神经网络的预测效果高出11 个百分点。

在上述方法中，BP 神经网络是应用最为广泛的神经网络模型，且它的预测效果较佳，所以选择BP 神经网络对上市公司的信用风险进行评估，并结合L-M 算法对网络进行优化以提高收敛速度。

一、 数据来源和指标筛选

(一)数据来源

将上市公司作为研究对象，遵循指标选取的系统性、科学性、客观性、可比性及可操作性等原则，从盈利能力、偿债能力、成长能力、营运能力这四个方面构建信用风险评估指标体系。 现从网易股票网站中的数据栏目①http：/ /quotes.money.163.com/old/＃query＝YLNL＆DataType＝yynl＆sort＝MGSY＿T＆order＝desc＆count＝25＆page＝0.随机截取了沪、深两市100 家上市公司2018 年的年报数据，其中包含了22个财务指标数据，如表1 所示。 这100 家上市公司中包含50家“非ST”企业，50 家“ST”或“∗ST”企业，满足数据选择的平衡性。 其中，“非ST”企业表示其财务状况良好，且信用评级较高，违约可能性较低，所以把这类企业划分为“低风险企业”；“ST”或“∗ST”企业表示其财务状况较差，且信用评级较低，违约可能性较高，所以又把这类企业划分为“高风险企业”。

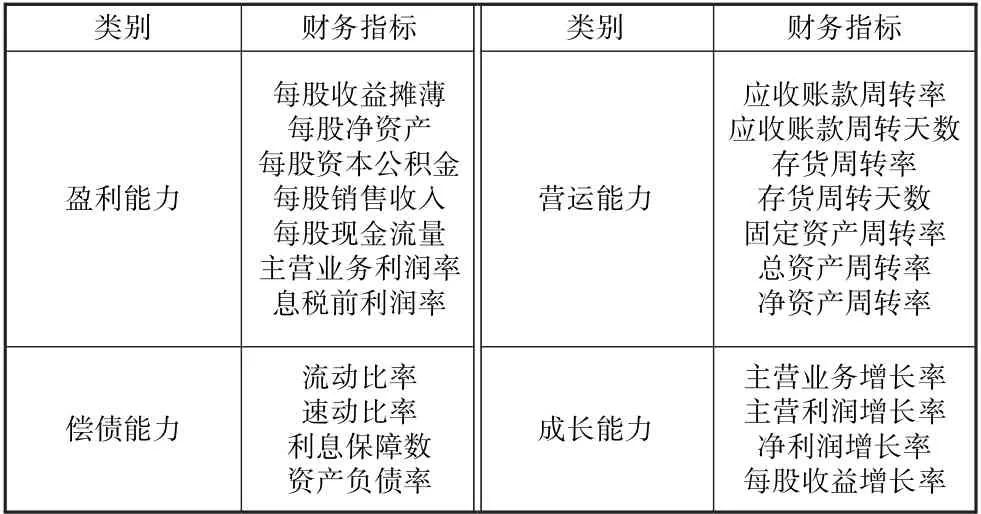
表1 财务指标体系

(二)指标筛选

由于上市公司的各个财务指标之间可能存在相关关系，导致信息重叠或冗余，不利于对研究问题的分析与开展，因此决定对22 个财务指标进行筛选，选择最能综合反映各公司财务状况的指标。

首先观察获取的22 个财务指标数据，发现每股净资产这项指标数据缺失过多，故删除该项指标，剩余21 个指标；随后利用SPSS 软件对缺失的数据进行补充，由于剩余的21个指标数据大部分完整或只存在少量缺失，故SPSS 中的5种替换缺失值的方法区别不大，此处选择“临近点的平均值”进行替换；最后可采用统计学中常用的因子分析法，将相同本质的变量归入一个因子，从而减少变量数目，以达到筛选指标的目的。

在进行因子分析前先利用SPSS 对100 家公司的21 个指标数据进行相关性分析，将相关度高的财务指标聚为一个大类，于是产生了13 个分类，分类结果如表2 所示。 每一个大类的指标都具备独立的代表意义，遵循指标选取的全面性原则，每个大类中的指标至少需要保留一个，故随后只需再利用SPSS 对前面5 个大类的指标数据进行因子分析，根据KMO 检验值大于0.6 且Bartlett 球体检验的显著性P值小于0.05 判断是否适合做因子分析，对于以上两个检验均通过的大类选择保留主因子载荷量最大的指标，剔除其余指标。 结果表明只有第一类和第二类指标数据适合做因子分析，检验结果如表3所示，这两类分别筛选出的两个指标为：息税前利润率、每股销售收入，其因子载荷矩阵分别如表4 和表5 所示。

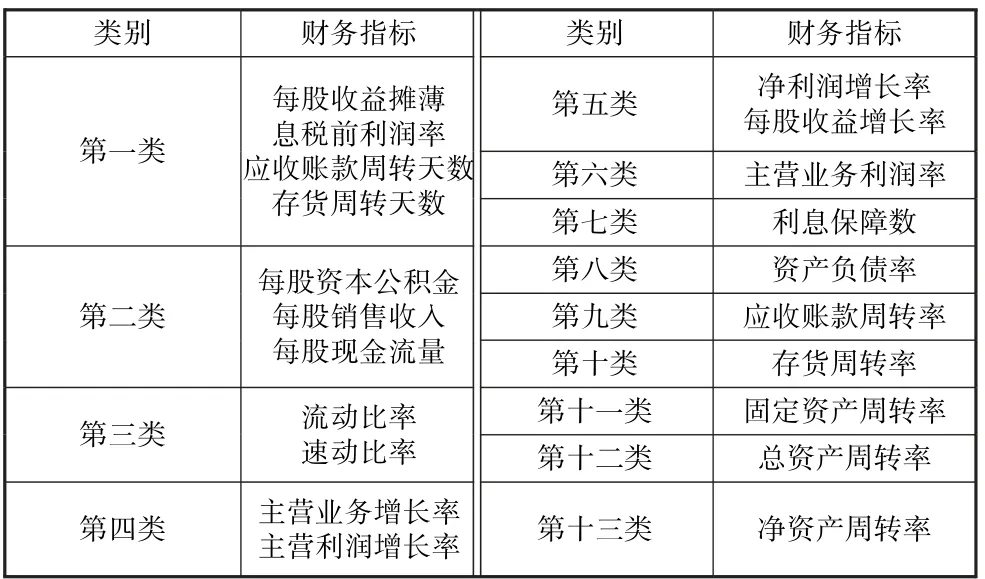
表2 财务指标分类结果

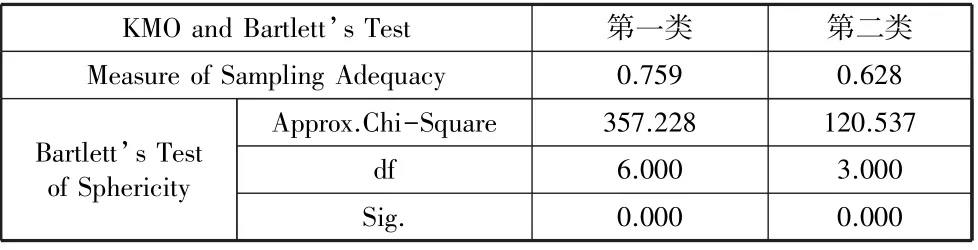
表3 KMO 与Bartlett 检验

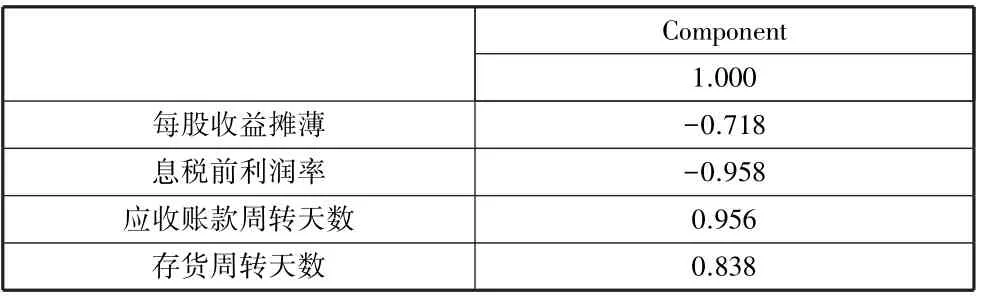
表4 第一类指标的因子载荷矩阵

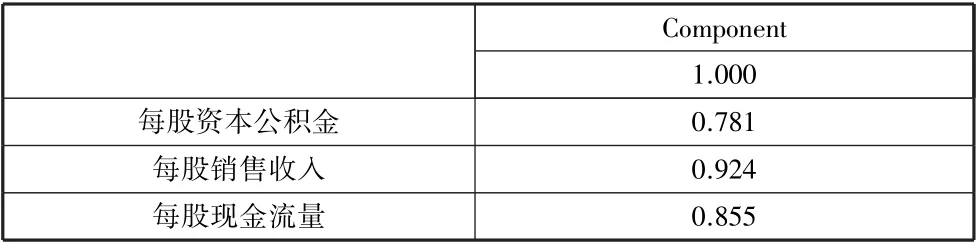
表5 第二类指标的因子载荷矩阵

因此，经过因子分析进行筛选后，最终保留16 个指标，分别为：息税前利润率、每股销售收入、流动比率、速动比率、主营业务增长率、主营利润增长率、净利润增长率、每股收益增长率、主营业务利润率、利息保障数、资产负债率、应收账款周转率、存货周转率、固定资产周转率、总资产周转率、净资产周转率。

二、 模型介绍

(一)BP 神经网络模型

BP 神经网络是1986 年由Rumelhart 和McClelland 为首的科学家提出的概念，它是一种多层前馈神经网络，主要特点为信息前向传递，误差反向传播，是目前应用较为广泛的神经网络之一。 由于BP 神经网络连接权值的调整是利用实际输出与期望输出的误差，对网络的各层连接权值由后向前逐层进行校正的计算方法，故将它称为反向传播学习算法，也简称BP 算法。 BP 神经网络的拓扑结构如图1 所示。

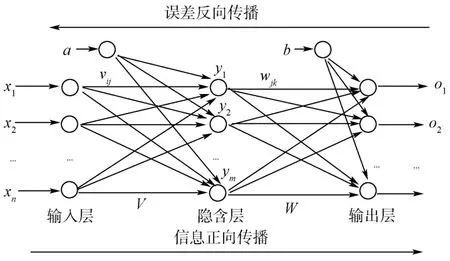
图1 BP 神经网络的拓扑结构图

由于目前并没有确切的文献研究说明BP 神经网络的层数越多拟合效果越好，故优先考虑三层网络，即含有一个输入层、一个隐含层、一个输出层。 对于简单的三层BP 神经网络模型，设网络的输入为X ＝ (x1，x2，…，xn)和期望输出为D ＝ (d1，d2，…，dl)，初始化各层神经元之间的连接权值为vij、wjk，初始化隐含层阈值为a，输出层阈值为b。 具体的学习算法及公式如下：

(1)隐含层输出计算

隐含层中第i 个神经元的输出为：

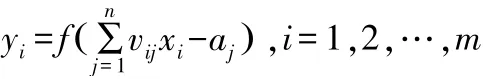
其中，m 为隐含层节点数，f ·( )为隐含层的传递函数，以下推导采用最为常见的Sigmoid 传递函数，即

(2)输出层的输出计算

输出层中第k 个神经元的输出可推导为：

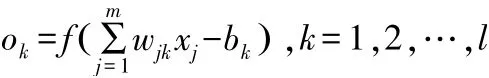
(3)误差计算

根据网络实际输出O 与期望输出D，计算网络总体误差E 为：

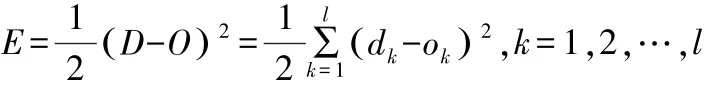
其中，期望输出D ＝(d1，d2，…，dl)，实际输出O ＝(O1，O2，…，Ol)。

(4)权值更新

根据网络总体误差E，更新网络连接权值vij、wjk的公式为：

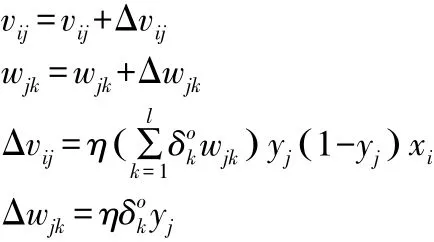
通过上述的BP 神经网络学习算法就可以对训练样本数据进行训练，通过误差反向传播，根据网络总误差是否达到精度要求来决定当前学习是否结束。

(二)L-M 算法优化模型

BP 神经网络无论在网络理论还是在性能方面都已比较成熟，由于其具有很强的非线性映射能力和柔性网络结构的优点让它被广泛运用。 但是传统的BP 算法是一种有监督的学习算法，采用的是负梯度下降算法，这种算法有两个明显的缺点，一个是收敛速度较慢，另一个是容易陷入局部极小值。针对这两个缺陷，出现了多种改进的BP 算法，如：动量反传的梯度下降法、动态自适应学习率的梯度下降法、弹性梯度下降法、L-M(Levenberg-Marquardt)法，在MATLAB 中的相应训练函数分别为：traingdm、traingda、trainrp、trainlm。 对于不同的实际问题，算法的选择也不同，主要取决于以下因素：训练样本的数量、网络权值和阈值的数量、网络的用途、误差目标要求等。 由于L-M 算法结合了梯度下降法和高斯-牛顿法，其收敛速度较快，均方误差较小，适合中小型网络的设计，故选择L-M 算法对传统的BP 神经网络进行改进。

L-M 算法允许在迭代的过程中沿着误差恶化的方向搜索，并且能够自适应地调整来改变权值，从而使网络更加有效。 L-M 算法的改进公式为：

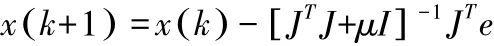
其中，比例系数μ>0 且μ 为常数，J 是误差对权值微分的雅克比矩阵，I 为单位矩阵，e 为迭代过程中的误差向量。

三、 实证分析

(一)划分数据集

参考尤璞等的研究成果，将选取的100 家上市公司作为样本，以3∶1 的比例划分为75 个训练样本(非ST 公司38 家，ST 或∗ST 公司37 家)，25 个测试样本(非ST 公司12 家，ST或∗ST 公司13 家)。

(二)归一化处理

由于不同的指标数据具有不同的单位尺度，如果直接输入模型会影响后续评估的准确性，故需要对数据进行归一化处理。 上述经筛选后的16 个指标中大部分为正向指标，中性指标有3 个，分别为：流动比率、速动比率、资产负债率，但由于选择的上市公司来源于各个行业，这3 个指标的适中值也会根据行业不同而有所区别，所以并不好统一一个适中值进行处理，并且在BP 神经网络中，为有效避开激励函数的饱和区以提高训练速度，一般要求输入数据的值在 -1，1[ ]之中，因此，此处选择如下的线性函数转换法：

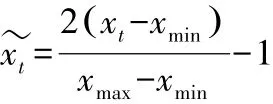
其中，xt代表原始样本数据，xmin和xmax分别代表样本数据中的最小值和最大值，代表归一化后的值。

(三)参数设计

现将建立一个三层的BP 神经网络模型，由于所选样本包含16 个指标，故输入层的节点数为16；输出层为所评估的上市公司的风险状态，可设置节点数为1，用二分类变量0-1表示，0 表示高风险的企业，即ST 或∗ST 的上市公司，1 表示低风险的企业，即非ST 的上市公司，实际操作中可将输出值与0.5 做比较，大于或等于0.5 的判定为低风险企业，其取值为1，小于0.5 的判定为高风险企业，其取值为0；隐含层的节点数可根据公式来确定，其中s 为隐含层的节点数，m 和n 分别为输入输出层的节点数，a 为1～10 之间的常数，故隐含层节点数范围在6～15 之间，经过多次尝试最终选择设置为10 的拟合效果最佳。 最大训练次数设置为1000，隐含层的激励函数设置为tansig 函数，输出层的激励函数设置为purelin 函数，训练函数设置为trainlm 函数，学习函数设置为learngdm 函数，误差函数设置为均方误差MSE，目标值设定为1×10-4，其余参数取默认值。

(四)结果分析

首先利用MATLAB 软件编写基于传统BP 算法的神经网络程序，将训练函数设置为traingd，其余参数设置如上所述值，运行后发现在设定的1000 次训练后无法达到收敛要求，于是逐渐增减训练次数，直至5000 次依旧无法达到收敛要求。 由于随着训练次数的增加，网络的收敛速度会越来越慢，故停止继续增加训练次数，尝试改变网络的误差值，经过多次运行发现误差设置为1×10-1时才终于完成收敛要求，此时的训练次数为2284 次，训练过程如图2 所示，该模型对于训练样本与测试样本的判定与预测结果分别如图3 和图4所示，为更加直观地分析模型的准确率，将上述结果总结如表6 所示。 观察图表，分析可知该模型的收敛速度较慢，预测准确率亦不高，为更好地评估对上市公司的信用风险，下面尝试对此模型进行改进。

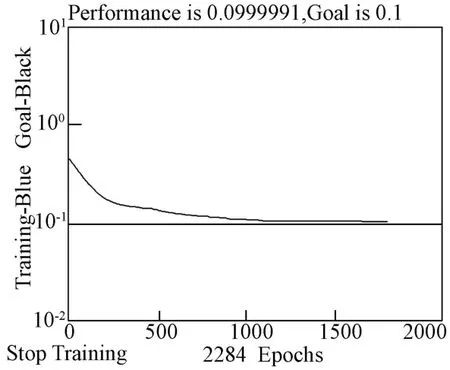
图2 traingd 函数训练过程

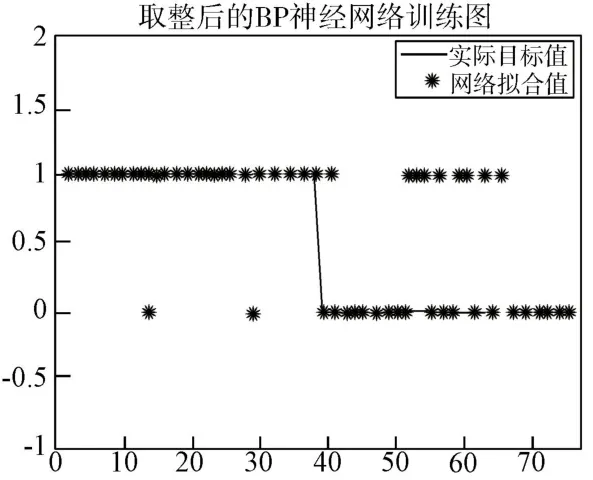
图3 traingd 函数下训练样本预测结果图

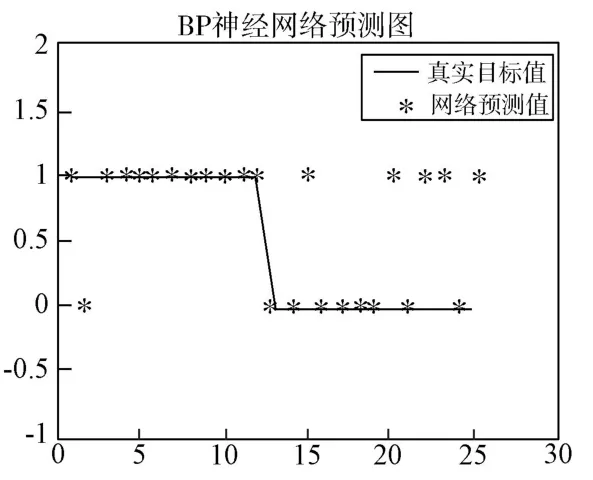
图4 traingd 函数下测试样本预测结果图

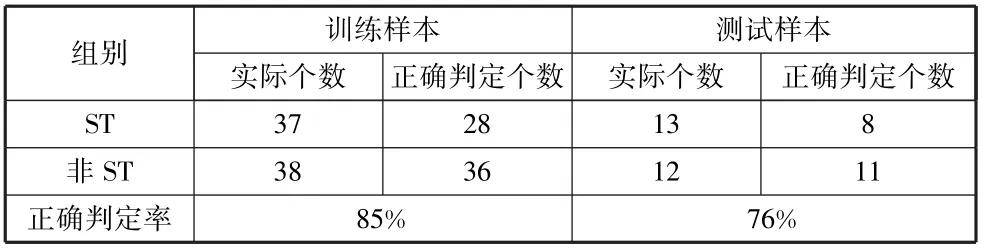
表6 传统BP 神经网络模型判定及预测结果表

再次利用MATLAB 软件编写优化后的BP 神经网络程序，将训练函数依次设置为traingdm、traingda、trainrp 和trainlm，其余参数值均按上述参数设计所述设置，训练过程分别如图5、图6、图7 和图8 所示，可以发现前三个训练函数下的网络经过1000 次训练后也没有达到收敛要求，只有trainlm函数下的网络经过了48 次训练就完成了所设定的误差目标值，收敛速度比较快，初步体现了基于L-M 算法优化后的BP神经网络对于上市公司风险评估研究的可行性。

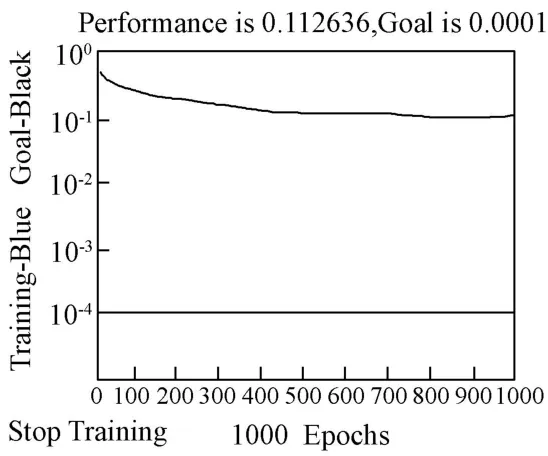
图5 traingdm 函数训练过程

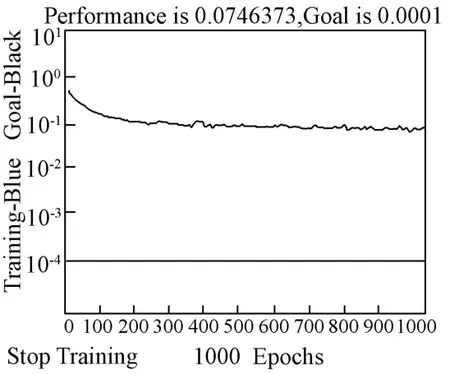
图6 traingda 函数训练过程

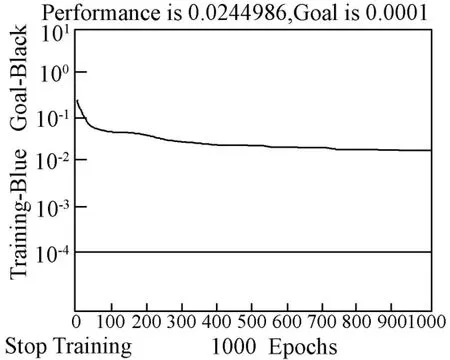
图7 trainrp 函数训练过程

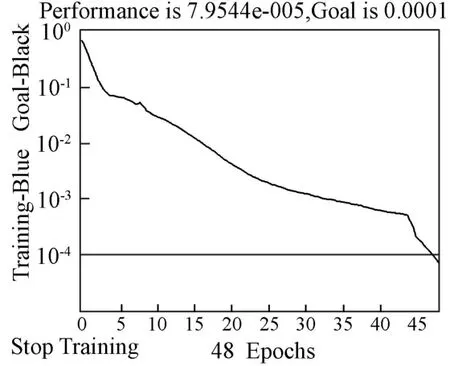
图8 trainlm 函数训练过程

接下来利用建立好的基于L-M 算法优化后的BP 神经网络对训练样本进行仿真模拟，随后再运用该网络对测试样本进行预测，从而综合分析检验此模型的应用准确性。 经过MATLAB 软件运行上述程序后，模型对于训练样本与测试样本的判定与预测结果分别如图9 和图10 所示，为更好地评判模型性能，将以上结果总结如表7 所示。

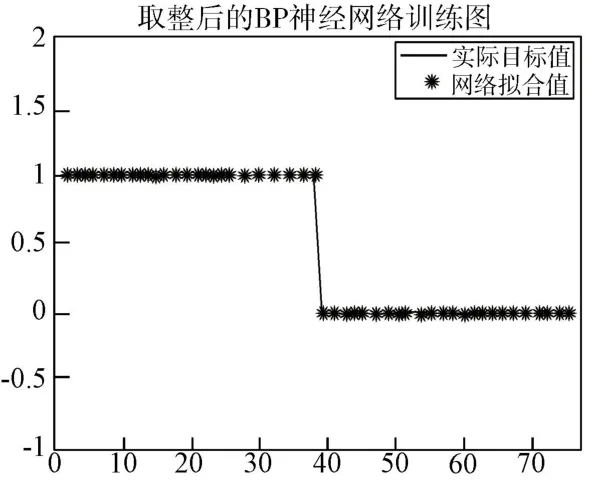
图9 trainlm 函数下训练样本预测结果图

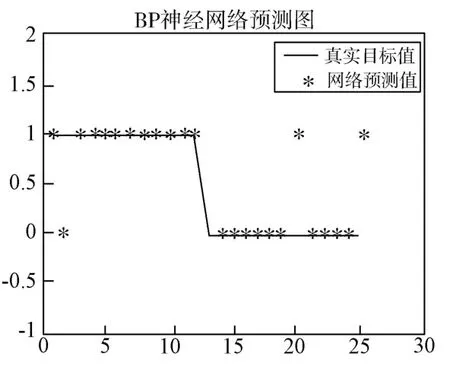
图10 trainlm 函数下测试样本预测结果图

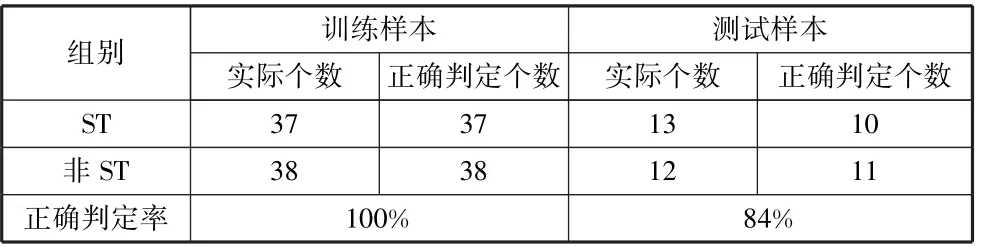
表7 L-M 算法优化后的BP 神经网络模型判定及预测结果表

观察上述结果，可以发现基于L-M 算法优化后的BP 神经网络对训练样本的预测准确率无论是对高风险企业还是低风险企业都是100%，进一步说明了其判断能力较好且准确率高，非常适合评估上市公司的风险状况；对测试样本而言，预测准确率为84%，也尚可接受。 与前文的传统BP 神经网络算法相比较，发现L-M 算法优化后的模型在收敛速度和预测准确率上均有明显的提升，充分体现了改进后模型的优势。

四、 结语

信用风险评估对于上市公司而言一直是一个重要的研究问题，可靠有效的评估结果不仅有助于投资者进行投资决策，同时也有助于企业内部的管理与改善，但目前依旧没有一个统一的评估方法供大家使用。 因此，可以运用人工智能中的BP 神经网络模型，并通过L-M 算法对它进行优化，建立一个合理且有效的信用风险评估模型。

但文章也存在一些不足，其一，由于所获取的数据必须真实可靠，评估结果才具备参考价值，但在实际操作中不能排除上市公司有做假账的可能性，这必定会对预测结果产生一定的影响；其二，在信用风险评价指标的选取上不够全面，上述所建立的模型仅仅是根据定量指标进行研究分析，而忽略了定性指标对于上市公司信用风险的考量也存在或多或少的影响。