基于R藤的Copula模型选择及应用

刘春婷

摘要：在实际生活中，高维数据的情形较多，常用的研究数据间相關关系的方法大多为传统的线性回归模型以及Logistic回归等，处理高维数据的方法涉及较少。基于上述分析，本文考虑采用Copula建模方法对高维数据进行分析，在Copula建模中较为重要的一点是对模型进行选择。因此本文考虑采用Copula模型中的R藤结构进行研究，通过选用贪婪算法来对R藤的模型结构进行选择，即对节点和Copula对函数类型进行确定。为了验证这一方法的可行性及适用性，通过陕西省城镇居民的消费数据进行实证研究，并得出相关结论。

关键词：高维数据;Copula函数;模型选择;相关关系

中图分类号：TP18            文献标识码：A

文章编号：1009-3044（2020）17-0222-03

随着时代的发展，越来越多的数据信息所产生，选择有效的方法对数据进行分析是至关重要的。Copula函数主要是用于刻画多个变量间的相关关系的，它不仅可以刻画协变量对响应变量的影响，还能够刻画协变量间的相关关系，克服了传统方法模型单一对数据中的信息挖掘不到位的缺点。Copula建模方法主要是选用不同的连接方式进行建模，常见的有C藤、D藤以及R藤，其中相比C藤和D藤而言R藤具有较高的灵活性，能够更加准确地描述变量间的相关关系，但是其涉及的连接种类多，计算量大成为了这一模型的难点。为了克服这一难点，本文考虑采用贪婪算法对R藤的结构进行选择。关键包含两个方面，一方面是对节点进行选择，即变量的位置关系进行选择，另一方面是对每两个节点间的Copula函数类型进行确定。

在Copula理论的发展过程中，它被广泛地应用到金融保险、投资组合以及风险预测等各个领域中，Rockinger和Jondeau（2001）[1]建立了Copula-GARCH模型对金融数据进行分析;杜子平（2009）[2]等将动态Copula和高维Vine Copula进行结合从而对不同国家证券市场间的关系进行分析。本文利用贪婪算法对Copula建模方法中R藤的模型结构进行选择，能够较快地得出R藤的具体模型结构，有效地降低了R藤模型算法的计算复杂度。

消费结构反映了一个地区的消费水平，也决定了当地人民的生活水平，具有较大的研究意义。近几年来，陕西省的综合实力不断上升，居民的消费水平也在发生着重要的变化，消费结构由较多的变量组成，为了更好地看出消费的各项指标间的相关关系，本文拟考虑采用刻画变量间相关关系具有极大优势的Copula建模方法进行研究，R藤的高度灵活性正好适用于这一实际问题。本文基于Copula建模方法采用R藤的方式进行建模，并对陕西省2009年至2018年的城镇居民消费数据进行研究。

1 相关理论基础

Copula函数是Sklar[3]在1959年提出的，他提出可以将一个多维的联合分布函数分解成多个边缘分布函数和一个连接函数，Copula函数就称为这个连接函数，通过该连接函数作为桥梁把边缘分布函数和联合分布函数进行连接。

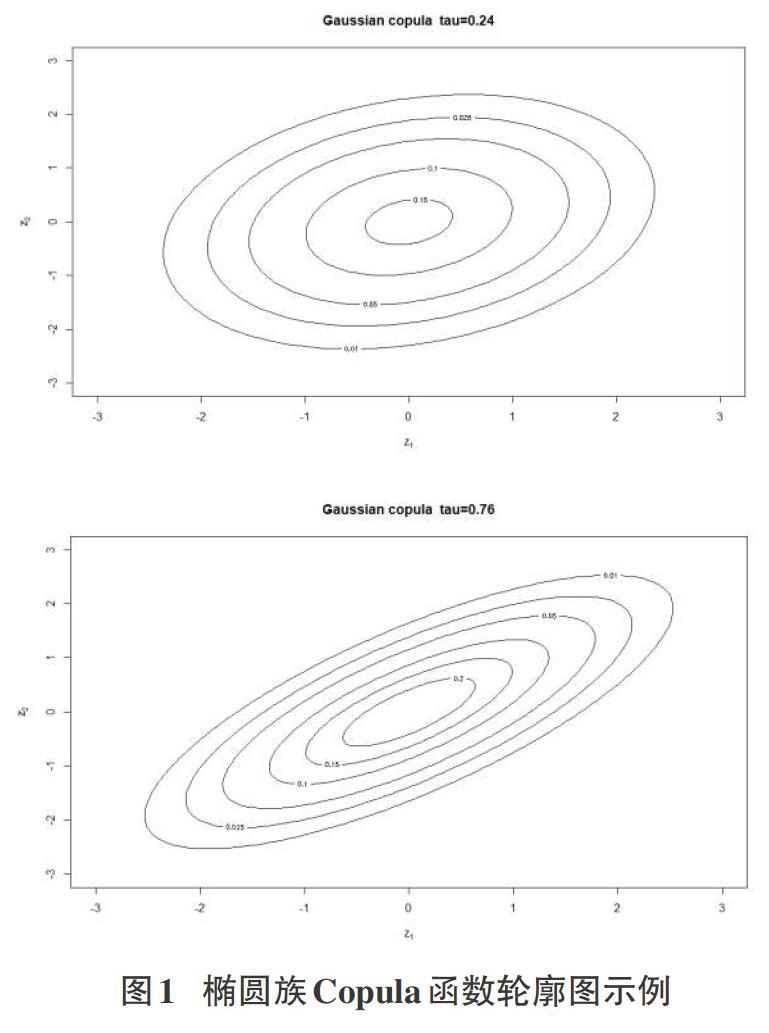
结合上述分析，将Copula函数进行分类，主要包含椭圆族Copula函数和阿基米德Copula函数两大类，它们用于刻画不同的数据特征，其中椭圆族Copula函数具有尾部对称的特点，其对应的轮廓图如下图1所示。

阿基米德族Copula函数尾部具有非对称性的特点，其对应的轮廓图如下图2所示。

因此对于不同的数据特征，要选用恰当的Copula函数类型进行刻画，这是R藤的模型建立过程中的一个难点。

Bedford & Cooke[4]于1999年提出，可以采用树的结构方式来直观的描述变量间的连接形式。其中用节点来表示变量，两个节点间的连线表示的是所选择的Copula函数类型。不同的连接方式得到不同结构的树，把这些树叫作规则藤，即R藤。R藤表现形式不按照一定的规则对节点间的位置关系进行排序，为了更加直观的进行说明，以一个4维变量为例，给出其中一种类型的R藤的表现形式。

对上式中的参数进行估计，主要采用分两步极大似然估计的方法，首先，对边缘分布函数中的参数进行极大似然估计，其次将边缘分布的参数估计结果带回，再利用极大似然估计对联合分布函数中的参数进行估计。

2 基于贪婪算法的模型选择

2013年，Dissman等人提出了一类处理高维离散型数据的贪婪算法[5]的方法，受该方法的启发，将该方法应用到数据为连续型的形势下，该算法的基本步骤如下。

1）估计边缘分布函数的参数

2） 从低阶节点出发，分别计算低阶节点涉及的所有的Copula对类型及参数值，进而以修正的赤池信息准则mAIC（modify Akaike Information Criterion）为判别标准，进一步筛选出节点间所有可能的结合方式当中最优的模型，再以上述最优模型的节点连接方式所得到的两两Copula对为下一步的起点。

3） 重复上述过程，直至将第[n-1]棵树的相关节点间的结合方式及每条边对应的Copula对类型确定。

3 实例分析

通过上述分析可知，Copula函数主要是用于对高维数据进行分析的，当数据的个数较多时，单一的考虑每个指标的变化规律不能够很好的刻画实际问题，因此可以通过Copula函数来考虑不同指标间的相关关系。陕西省城镇居民的消费结构由8个指标组成，那么除了单一的研究每年指标的变化规律外，观察不同指标间的相关关系是十分具有价值的。因此本文选取陕西省2009年至2018年的城镇居民消费数据，其中包含如下8个指标。

各个指标是如何发展的，通过如下变化趋势图能够直观的得出结果。

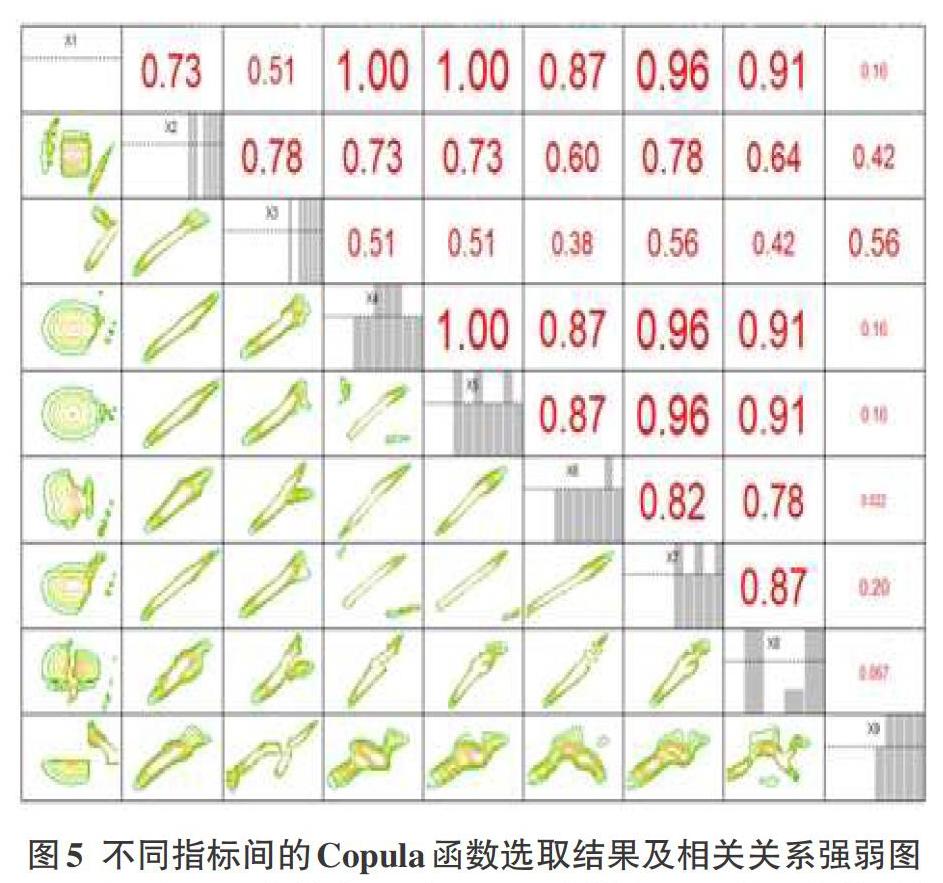
从图4只能大致看出各项指标的发展趋势以及发展趋势的强度，但是具体不同指标之间是否有相关关系，值得进一步研究。通过对数据观察不难发现，指标的个数较多，且数据大多呈现出不对称的特征，因此采用本文所建立的处理高维数据的Copula函数模型是极具优势的。为了更加全面的分析各指标间的相关关系，将年份也作为一个变量进行研究，同时对9个变量进行分析，通过贪婪算法对R藤的模型结构进行选择，所得到的结果如下图5所示。

图5为通过贪婪算法对Copula建模方法下的R藤的選择结果，本文主要研究第一层树，即对不同变量间的关系进行刻画。其中图的左下方描述的是所选用的Copula函数拟合出的轮廓图，从图上可以看出，指标衣着与医疗保健、交通通讯与文教娱乐与通讯等指标对之间呈现出较强的尾部对称性，并且从轮廓图的形状上来看，越扁的说明两个指标的相关性越强。图的右上方这些数字刻画了每两个变量间的相关性强弱，相关性越强这个红色的字体越大并且对应的数的绝对值越接近于1，相关性越弱，对应的数的绝对值越接近于0。为了更加直观的得出不同指标间的相关关系，给出具体数值见表2。

表2 详细地给出了每两个变量间的相关关系结果，由表中数据易得，（1）变量1年份与任意指标之间都具有较高的相关性，尤其是与食品和衣着这两个变量，呈现出较高的正相关性，说明人们的生活水平在不断提高，大家对衣着和食品方面的支出越来越大。（2）食品与家庭设备及服务这两项指标之间呈现出负相关性，且kendall [τ]值为-0.63，说明相关程度较高;并且衣着与家庭设备及服务这两项指标也呈现出负相关性，说明家庭设备及服务该指标的增长速度与它们之间是呈现负相关关系的。（3）医疗保健和交通通讯、文化娱乐及服务以及杂项商品及服务、医疗保健与文教娱乐及服务等等，它们之间都呈现出较高的正相关性，相关性都较强。（4）观察不难发现，居住这项指标与各指标间的关系均不是太强，但是它的增长幅度从数据中可以看出，具有较大的增长幅度，说明该项指标不受其他因素的影响，自身的涨幅较大，说明大家对居住越来越重视。

参考文献：

[1] Coutant S，Jondeau E，Rockinger M.Reading PIBOR futures options smiles：The 1997 snap election[J].Journal of Banking & Finance，2001，25（11）：1957-1987.

[2] 杜子平，闫鹏，张勇.基于“藤”结构的高维动态Copula的构建[J].数学的实践与认识，2009，39（10）：96-102.

[3] Genest C，MacKay J.The joy of copulas：bivariate distributions with uniform marginals[J].The American Statistician， 1986，40（4）：280.

[4] St?ber J，Joe H，Czado C.Simplified pair copula constructions—Limitations and extensions[J].Journal of Multivariate Analysis， 2013，119：101-118.

[5] 常友渠，肖贵元，曾敏.贪心算法的探讨与研究[J].重庆电力高等专科学校学报，2008，13（3）：40-42，47.

【通联编辑：唐一东】