一种粗糙神经网络的Simulink仿真研究

常志玲 赵旭鸽

摘要：本粗糙神经网络由三层构成，其输入层由上下两个经典神经元构成的粗糙神经元组成，并与隐层之间为全连接，隐层与输出层也为全连接，用离散并约简后的一对输入向量的边界值作为输入向量。对于这种粗糙神经网络，利用Simulink工具进行了仿真，并详细叙述了整个建模过程，用经典实例进行了验证，实例表明本建模工具能够快速准确地处理复杂的粗糙神经网络问题，并且参数设置也比较方便。

关键词：变精度粗糙集;神经网络;Simulink;分类算法

中图分类号：TP391        文献标识码：A

文章编号：1009-3044（2020）17-0007-03

Abstract： A rough neural network is made up of three layers， input layers are made up rough neurons， and each rough neuron is made up of a pair of typical neurons， and each input vector is a pair of boundary values of discrete interval of each condition attribute. The rough neurons of input layers and the typical neurons of hidden layers are linked completely， and the typical neurons of hidden layers and the typical neurons of output layers are linked completely too. The inconsistent decision table is reduced by the reduction algorithm based on variable precision rough set， and the input vectors of neural network is reduced on a large scale. It is simulinked by matlab/simulink. The experimental results show that the Simulink tool can deal with the complex rough neural network problem quickly and accurately， and the parameter setting is convenient.

Key words： variable precision rough; neural network; simulink; classification algorithm

在处理现实中的不完整性和不确定性信息方面，最有效的工具就是粗糙集理论[1]和神经网络[2]。粗糙集理论在处理不确定性数值方面具有强大分析能力，神经网络在处理问题方面具有高速寻找优化解的能力。但是当问题比较复杂，神经网络输入数据的维数就会很高，结构就比较复杂，而粗糙集理论能很好地约简掉输入数据的冗余，能够把复杂问题简单化。另外粗糙集理论的泛化性能和容错性比较弱，但是神经网络的泛化能力、自组织能力和抗干扰能力强，所以二者结合具有很好的互补性。因此很多人把二者结合起来进行研究，用于改善神经网络的拓扑结构[3，4]，并取得了很好的性能。可是这些成果几乎都把神经网络的输入向量问题考虑在外，实际上神经网络的预测性能直接受输入向量的影响。

目前，主要有两类粗糙集理论和神经网络的结合：一类结合由粗糙集理论先对数据约简，去掉冗余信息，然后再构造神经网络进行训练[5];另一类结合通过构造粗神经元[6]，增加系统的泛化能力和容错性能。但是两种网络结构都没有考虑输入向量的选择问题，因此有时输入向量的选择不合理也会造成训练结果的不理想。文献[7]考虑了神经网络的输入向量的选择，构造出一种新的粗糙神经网络拓扑结构，由粗糙神经元和经典神经元混合组成，不但考虑了神經网络的拓扑结构，而且对输入向量做了详细研究，能够克服现有方法的缺点。本文在此基础上使用Matlab中的Simulink实现了建模，并叙述了详细的过程。

1 粗糙神经网络

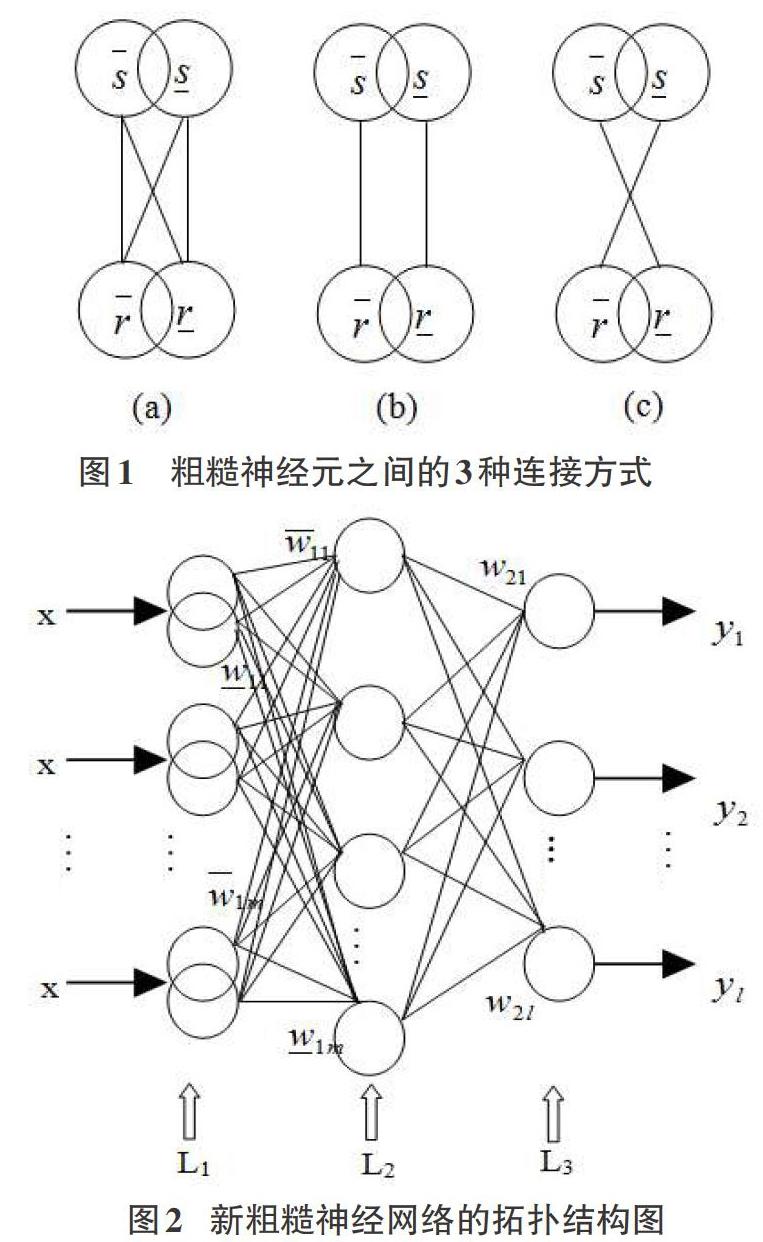
粗糙神经网络（Rough Neural Network， RNN）[8]由粗糙神经元和经典神经元彼此互相连接而成。一个粗糙神经元[r]在神经网络中由一对神经元组成，其中一个神经元[r]称为上边界，另一个神经元[r]称为下边界。两个粗糙神经元之间有2个连接或4个连接，因此共有3种可能的连接，如图1所示。上下边界神经元之间的连线表示这两个神经元信息的交换，其中（a）图有4条连线，表示粗糙神经元[r]和粗糙神经元[s]之间为全连接，（b）图和（c）图都只有2条连线，表示有两种连接，其中（b）图表示粗糙神经元[r]激励粗糙神经元[s]，（c）图表示粗糙神经元[r]抑制粗糙神经元[s]。

粗糙神经网络的拓扑结构和经典神经网络的拓扑结构一样由输入层、隐层和输出层组成，只是其神经元除了经典神经元还有粗糙神经元，外界的信息通过输入层输入，经过网络训练后由输出层输出到外界环境。

2粗糙神经网络构造描述

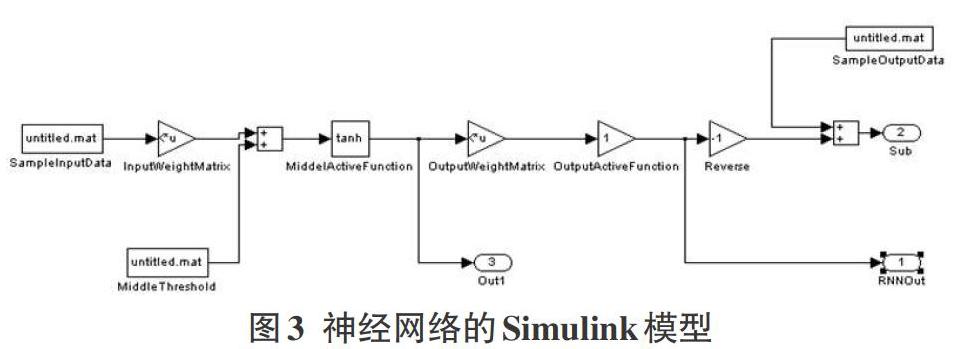
为了简化神经网络的复杂性，首先把输入的属性集合进行约简，采用的算法是基于变精度粗糙集上下分布约简[9]，设约简后有[m]个属性，则输入层L1构造[m]个粗糙神经元，由于本粗糙神经网络对输入向量是有选择性的，由每个条件属性值经离散后其区间的形成的一对边界值作为输入向量，如对象[i]在属性[j]上经离散后形成的区间为[[xij，xij]]，其中[xij≤xij]，那么在第[j]个粗糙神经元输入的数值为[xij=（xij，xij）]; 隐层L2由经典神经元构成;L1和L2之间为全连接;输出层L3也有经典神经元构成，表示决策属性值经训练后的输出，L2和L3也为全连接。所构造的粗糙神经网络的拓扑结构如图2，粗糙神经网络由三层构成。具体算法的描述见文献[7]。

3 粗糙神经网络Simulink仿真模型的建立

Matlab中的Simulink是非常有用的仿真工具，比如用在机器人等领域的仿真[10]，就取得了很好的效果。目前采用的神经网络算法也很多，最常用的有BP算法，基于径向基网络的算法[11]。本粗糙神经网络根据图2所示的粗糙神经网络的拓扑结构，使用Simulink所创建的粗糙神经网络模型如图3所示，采用BP算法，其中的模块设置为：SampleInputData输入层模块，为输入学习模式提供输入接口;InputWeightMatrix是权值模块，输入层L1到隐层L2的连接权由初始权值随机产生;隐层L2单元和输出层L3单元的阈值由Middle Threshod产生;隐层L2传递函数模块是MiddleActiveFunction，采用tan-sigmond型函数tansig（），根据输入层的输出和权值求出隐层的输入并求出隐层的输出，使用Out1模块存储隐层输出数据;OutputWeightMatrix是权值模块，初始权值随机产生，为隐层到输出层的连接权值;OutputActiveFunction是输出层传递函数模块，采用purelin（）函数，根据隐层的输出和权值及阈值求出输出层的输入并求出输出层实际输出，并存储在SampleOutputData模块中，Sub减法模块，用来实际输出和期望输出做比较求误差，然后根据实际情况对权值和阈值进行调整，进行再次训练;RUNOut模块是实际输出和期望输出的误差分析模块。直到训练到误差在规定的范围内，或满足了训练的次数之后停止训练。

4实例分析

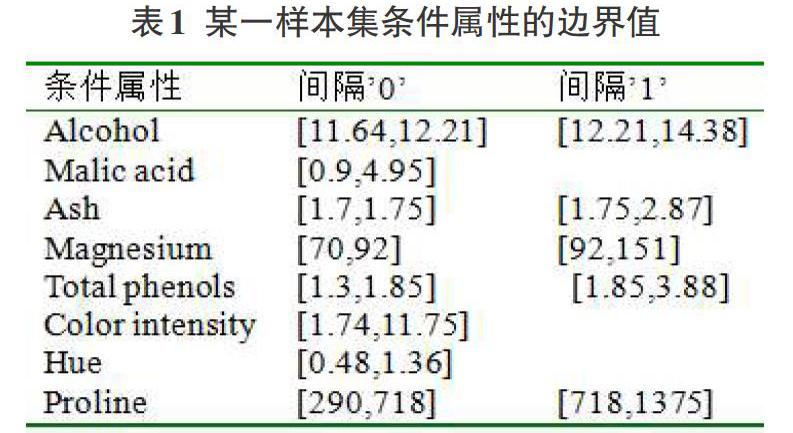
本实验对UCI[12]数据集进行分析，选取葡萄酒数据样本为实验数据，其样本共有178个，每个样本有条件属性13个，决策属性1个，并利用本算法进行了规则获取实验。不失一般性，本实验使用Rosetta工具从180个样本中随机选取60个样本作为实验数据，为了简化实验过程，随机选取Alcohol、Malic acid、Ash、Magnesium、Total phenols、Color intensity、Hue、Proline 8个条件属性作为数据集的条件属性集，每个属性值都没有缺失值且连续，最终形成一不一致决策表。不失一般性，反复使用Rosetta随机选取60个样本中的36个样本作为训练集，剩余24个样本作为测试集。并且对所有样本采用GDM方法进行离散化，选取其中某一组的条件属性离散化后的边界值如表1所示，采用基于VPRS的上下分布约简算法对训练集样本进行约简。其中[β]的取值采用An[13]的方法，其取值为[0.5<β≤1]，[β]为正确分类率。以[β∈（0.5，0.667]]作为例子，并使用如表1所示的约简之后的边界值作为每一个粗糙神经元的输入值。

针对本实例，使用图3粗糙神经网络进行训练，由每个属性的离散化后的边界值组成的训练样本记为S2，测试样本记为T2，根据S2和T2的实际情况，S2的输入样本含有4个条件属性，每个样本有4对输入向量，因此其中输入层根据约简属性集属性设置为4个粗糙神经元，隐层神经元个数根据输入层神经元的个数和隐层神经元的个数的关系设置成9个神经元，输出层由决策属性的取值决定，设置成3个神经元，分别用输出[[100]']表示输出第1类，输出[[010]']表示输出第2类，输出[[001]']表示输出第3类。采用本粗糙神经网络BP算法对实例进行训练，设定训练次数为1000，误差精度为[10-6]。为了计算方便，避免由于各训练样本的数量级差别很大以至于部分神经元达到过饱和状态，所以对样本的训练集和测试集进行归一化处理[14]，其网络训练误差如图4，经过679步达到预期目标，经分析可知，除了1个样本外，其他样本在[β∈（0.5，0.667]]之间都能正确分类，并且实际输出和期望输出的误差趋近0，因此可以计算出其正确分类率达到95.83%。

5结束语

针对考虑了输入向量的选择的复杂粗糙神经网络结构，使用了Matlab中的Simulink工具对其进行了建模，并详细叙述了整个建模过程，用经典实例进行了验证，实例表明本建模工具能够快速准确地处理复杂的粗糙神经网络问题，并且参数设置也比较方便。

参考文献：

[1] Pawlak Z.Rough sets[J].International Journal of Computer & Information Sciences， 1982，11（5）：341-356.

[2] 杨建刚.人工神经网络实用教程[M].杭州：浙江大学出版社，2001.

[3] 何明，李博，马兆丰，等.粗糙集理论框架下的神经网络建模研究及应用[J].控制与决策，2005，20（7）：782-785.

[4] 许志兴，丁运亮，陆金桂.一种基于粗糙集理论的粗糙神经网络构造方法[J].南京航空航天大学学报，2001，33（4）：355-359.

[5] 郭志军，何昕，魏仲慧，等.一种基于粗糙集神經网络的分类算法[J].计算机应用研究，2011，28（3）：838-840，850.

[6] Liu H J，Tuo H Y，Liu Y C.Rough neural network of variable precision[J].Neural Processing Letters， 2004，19（1）：73-87.

[7] 常志玲，王全喜.一种新的粗糙神经网络的构造算法研究[J].计算机时代，2009（4）：52-54.

[8] 王玮，蔡莲红.基于粗集理论的神经网络[J].计算机工程，2001，27（5）：65-67.

[9] 米据生，吴伟志，张文修.基于变精度粗糙集理论的知识约简方法[J].系统工程理论与实践，2004，24（1）：76-82.

[10] 叶长龙，张思阳，于苏洋，等.基于神经网络的全方位移动机器人运动稳定性研究[J].机器人，2019，41（4）：443-451.

[11] 陈雅颂，汪晓银，安子韩，等.PVDF分离膜性能径向基网络仿真模型的建立与应用[J].长江大学学报（自科版），2018，15（17）：9-14，4.

[12] The Center for Machine Learning and Intelligent Systems. UC Irvine Machine Learning Repository[DB/OL]. 2007-07-21/2007-10-07. http：//archive.ics.uci.edu/ml/datasets.html.

[13] An Ai-jun， Shan Ning， Chan Christine et al. Discovering rules for water demand prediction： An enhanced rough-set approach[J]. Engineering Applications of Artificial Intelligence， 1996， 9（6）：645-653.

[14] 柳小桐.BP网络输入层数据归一化研究[J].机械工程与自动化， 2010，6（3）：122-123.

【通联编辑：唐一东】