中职学校多学科课程交叉教学的思考

王静

摘要：为培养合格的中等职业学校人才需要从多学科进行多门课程科学合理的设置。在当前的教学环节中，不同的课程之间很少进行知识点的交叉引用和应用，学生较难跨课程形成系统的知识。本文以图形图像编辑课程为例，引用数学课程的知识点进行教学，通过实践实现多课程教学，提高学生综合應用知识的能力。

关键词：课程设计;多学科;图形图像;数学

中图分类号：TP319          文献标识码：A

文章编号：1009-3044（2020）17-0154-02

教育部发布《关于职业院校专业人才培养方案制订与实施工作的指导意见》中指出，中等职业学校应当将思想政治、语文、历史、数学、外语（英语等）、信息技术、体育与健康、艺术等列为公共基础必修课程，并将物理、化学、中华优秀传统文化、职业素养等课程列为必修课或限定选修课。图像处理课程是电子商务、计算机应用、广告设计以及网络等专业的中职学校必修课。Photoshop是目前世界上最优秀的图形图像处理软件之一，是事实上的行业标准，通常是图形图像课程选择授课的软件。职业学校计算机教学的特点是强调操作性和实用性，本课程属于实操型课程，其教学目标是熟练运用Photoshop进行各种相关工作。具体分为基础技能、单一功能应用和多功能复合效果等三个层次的目标。当前的教学过程中通过大量反复练习，学生都能较快地掌握其操作技巧，实现第一层次和部分第二层次目标。但对已学知识遗忘得也较快，尤其较难形成灵活运用工具、命令或操作方法解决问题的能力，较难实现第二第三层次目标。

造成这个问题的原因，一是学生只知其然而不知其所以然。通过进行大量的实践训练，仅实现了授人以鱼，而没有达到授人以渔。要掌握相应操作方法和技能并能灵活运用，需要从理论上理解工具或命令的功能实现的原理和基本操作方法的基本思想。理论指导实践是其中一项重要的教学方法。开展理论指导就需要跳出本课程的教学范围，将涉及的数学、物理、光学乃至美学等理论与课程的具体操作结合起来，提高学生解决问图形图像编辑技术题的能力。

1 数学知识对于图形图像编辑的重要意义

图像处理是指对图像进行分析、加工和处理，使其满足视觉、心理或其他要求的技术。计算机和软件并不能认识图形和色彩，图像处理软件处理或创建的对象就是数据，在计算机中描述的图像以像素作为基本元素以数字方式存贮。它由矩阵形式的像素点组成。如一幅分辨率为640×480的图像是指该图像水平方向（每行）上有640个像素点，竖直方向（每列）上有480个像素点，该图像共由307200个像素点构成，每个像素点的颜色不同，就构成了整幅图像。数字图像的处理过程离不开计算机算法，而数学知识是计算机算法的重要基础。理解相关操作的数学知识，对于掌握其实现原理和操作技能对提高能力有较大的帮助。钢笔工具、滤镜、变换等操作背后都是一系列的数学知识，本文从这些示例说明数学知识与图形图像知识的交叉教学的可能性和其积极意义。

2 钢笔工具与贝塞尔曲线

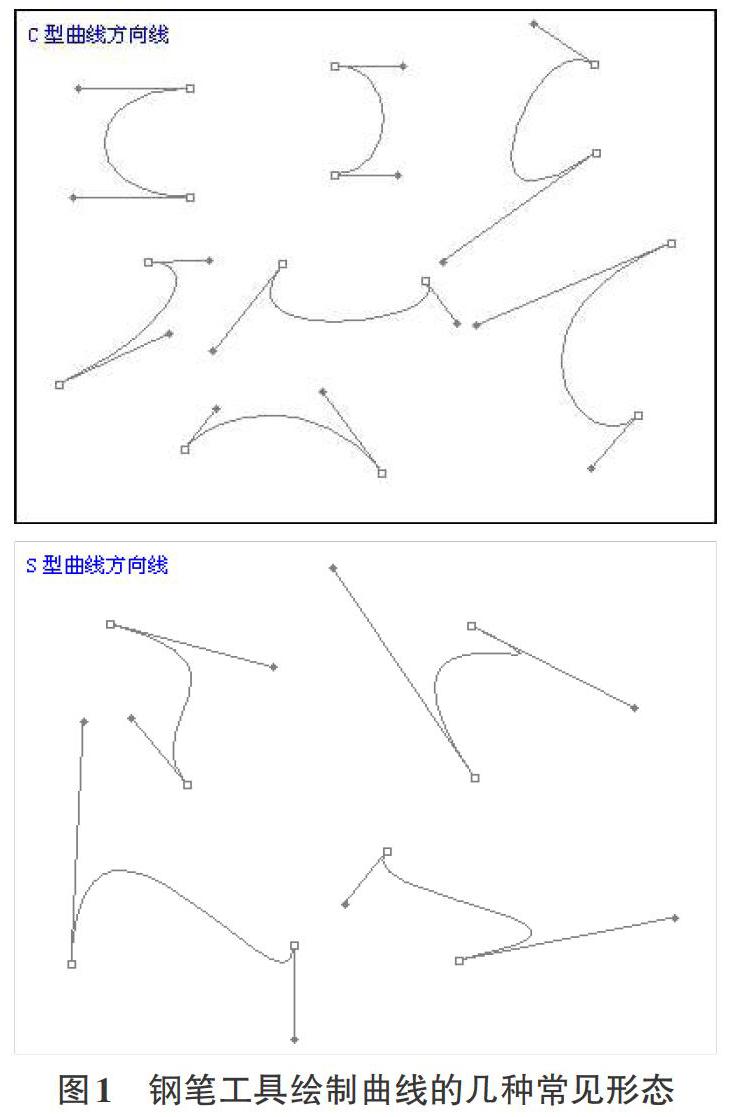
通过钢笔工具，可以直观地绘制曲线和直线段、精确绘制直线段和曲线，还可以用于绘制路径，就像用铅笔在纸上绘图一样。也可以组合使用钢笔工具和形状工具以创建复杂的形状。对于很多Photoshop初学者来说钢笔工具是一个非常不友好的存在，不少的初学者都卡在了钢笔工具的操作上。如果能理解了钢笔工具背后实际是各种贝塞尔曲线（Bézier curve）的组合，就会有利于理解和吃透这个工具。

贝塞尔曲线是计算机图形学中相当重要的参数曲线。由于需要点阵化更精细的分辨率时，重新插值（补点）的计算量较小，贝塞尔曲线被广泛地在计算机图形中用来为平滑曲线创建模型。贝塞尔曲线是部分矢量图形文件和相应软件（如PostScript、PDF等）能够处理的唯一曲线，用于光滑地近似其他曲线。最常用的是二次和三次贝塞尔曲线。

钢笔工具中的锚点实际上就是贝塞尔曲线中线段的起点，通过拖动锚点就是调节贝塞尔曲线的方向和其弯曲度。只要学生掌握这个原理，再多加操作和练习，就可以熟练地掌握这个工具。

3 各种变换的基本数学基础

图像处理中的变换是图形图像编辑中常用的基本操作，常见的类型包括缩放、旋转和翻转、变形、斜切、扭曲、透视。

几何变换是指从具有几何结构之集合至其自身或其他此类集合的一种对射。具体来说，“几何变换是一个函数，其定义域与值域为点集合。几何变换最常见的定义域与值域为同时为R2，或同时为R3。其他的几何变换则要求须为一对一函数，使之有反函数。”可透过研究这些变换的方法来研究几何。

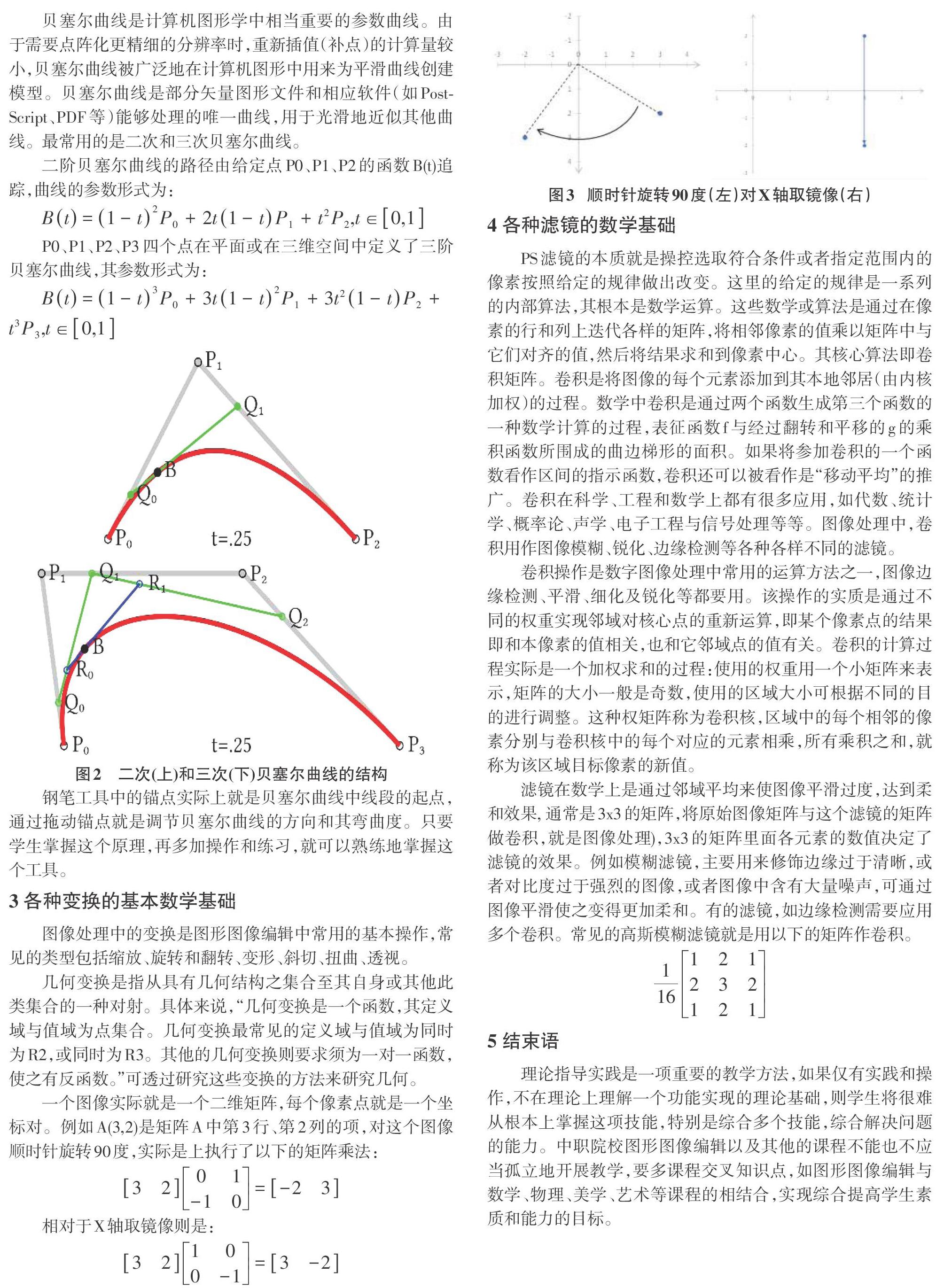
一个图像实际就是一个二维矩阵，每个像素点就是一个坐标对。例如A（3，2）是矩阵A中第3行、第2列的项，对这个图像顺时针旋转90度，实际是上执行了以下的矩阵乘法：

4 各种滤镜的数学基础

PS滤镜的本质就是操控选取符合条件或者指定范围内的像素按照给定的规律做出改变。这里的给定的规律是一系列的内部算法，其根本是数学运算。这些数学或算法是通过在像素的行和列上迭代各样的矩阵，将相邻像素的值乘以矩阵中与它们对齐的值，然后将结果求和到像素中心。其核心算法即卷积矩阵。卷积是将图像的每个元素添加到其本地邻居（由内核加权）的过程。数学中卷积是通过两个函数生成第三个函数的一种数学计算的过程，表征函数f与经过翻转和平移的g的乘积函数所围成的曲边梯形的面积。如果将参加卷积的一个函数看作区间的指示函数，卷积还可以被看作是“移动平均”的推广。卷积在科学、工程和数学上都有很多应用，如代数、统计学、概率论、声学、电子工程与信号处理等等。图像处理中，卷积用作图像模糊、锐化、边缘检测等各种各样不同的滤镜。

卷积操作是数字图像处理中常用的运算方法之一，图像边缘检测、平滑、细化及锐化等都要用。该操作的实质是通过不同的权重实现邻域对核心点的重新运算，即某个像素点的结果即和本像素的值相关，也和它邻域点的值有关。卷积的计算过程实际是一个加权求和的过程：使用的权重用一个小矩阵来表示，矩阵的大小一般是奇数，使用的区域大小可根据不同的目的进行调整。这种权矩阵称为卷积核，区域中的每个相邻的像素分别与卷积核中的每个对应的元素相乘，所有乘积之和，就称为该区域目标像素的新值。

滤镜在数学上是通过邻域平均来使图像平滑过度，达到柔和效果， 通常是3x3的矩阵，将原始图像矩阵與这个滤镜的矩阵做卷积，就是图像处理），3x3的矩阵里面各元素的数值决定了滤镜的效果。例如模糊滤镜，主要用来修饰边缘过于清晰，或者对比度过于强烈的图像，或者图像中含有大量噪声，可通过图像平滑使之变得更加柔和。有的滤镜，如边缘检测需要应用多个卷积。常见的高斯模糊滤镜就是用以下的矩阵作卷积。

5 结束语

理论指导实践是一项重要的教学方法，如果仅有实践和操作，不在理论上理解一个功能实现的理论基础，则学生将很难从根本上掌握这项技能，特别是综合多个技能，综合解决问题的能力。中职院校图形图像编辑以及其他的课程不能也不应当孤立地开展教学，要多课程交叉知识点，如图形图像编辑与数学、物理、美学、艺术等课程的相结合，实现综合提高学生素质和能力的目标。

参考文献：

[1] 中华人民共和国教育部.关于职业院校专业人才培养方案制订与实施工作的指导意见[M/OL]. [2020-02-02].http：//www.moe.gov.cn/srcsite/A07/moe_953/201906/t20190618_386287.html

[2] 维基百科.贝塞尔曲线[M/OL].[2020-02-02]. https：//zh.wikipedia.org/wiki/%E8%B2%9D%E8%8C%B2%E6%9B%B2%E7%B7%9A

[3] 刘雄伟，王晓.初等数学在数字图像处理中的应用两例[J].中国教育信息化，2013（8）：39-41.

[4] 黎小辉.数学知识在《Photoshop图形图像处理》中的应用[J].教育教学论坛，2010（36）：177-178.

[5] 孔红亮.数学方法在Photoshop教学中的应用——浅析图层混合模式的教学[J].科技信息（学术研究），2007（31）：547+551.

[6] 张庆丰.弱数学要求的数字图像处理教学[J].大学教育，2014（2）：75-77.

[7] 靳玉军.中职院校PhotoShop课程教学浅谈[J].电脑知识与技术，2016，12（21）：124-125.

【通联编辑：王力】