基于全局稳定的爬壁机器人双环轨迹跟踪控制

滕 昊，庄 园，邓世建+

(1.中国矿业大学 信息与控制工程学院，江苏 徐州 221008；2.云南民族大学 电气信息工程学院，云南 昆明 650540)

0 引 言

对期望轨迹跟踪控制是爬壁机器人作业的基础，本文依托磁吸附轮式移动爬壁机器人对轨迹跟踪控制进行分析研究，考虑到现爬壁机器人轨迹跟踪控制中主要面临3个难点[2-4]：跟踪精度差、控制响应速度慢以及系统状态不稳定问题。

考虑将航向角加入到系统的反馈控制中，即采用位置反馈加上姿态(航向角)反馈，在航向角为预期的前提下再到达指定位置，可有效保证控制精度；而对于响应控制问题，目前所应用的控制算法主要有如下所示：

(1)非线性状态反步控制法[5-8]：通过建立数学模型，根据稳定性条件，反推控制律使得实际轨迹和期望轨迹之间的误差收敛，以准确跟踪期望轨迹，由于这种方法响应速度较慢，跟踪误差收敛的时间较长，且对于不确定参数没有较强的适应性，所以，在实际应用中，存在较大的局限性。

(2)自适应反步法[9]：为解决反步法中的不确定参数无法估计的问题，自适应反步通过滤波器反馈信号并对不确定参数进行在线估计，将估计的值最后用反步法得到受约束的控制律，作用于控制系统作用，反复自调整、自适应最终实现稳定的轨迹跟踪。但该方法的计算十分复杂庞大，工作效率较低。

(3)滑模跟踪控制法[10-12]：对于模型已知的控制系统，通过设计趋近律使得控制误差快速收敛，迫使系统按照预定“滑动模态”的状态轨迹运动。由于滑动模态可以进行设计且与对象参数及扰动无关，这对于轨迹跟踪控制具有较强的鲁棒性。

综合以上分析，滑模控制算法具有易于控制而且鲁棒性强的特点对于爬壁机器人在现场不确定复杂环境下更加适用。但是滑模控制算法虽然具有较快的响应速度与一定的鲁棒性，但是系统内部的不确定参数需要根据系统的特征做进一步处理。基于此，本文以运动学模型为基础，对爬壁机器人轨迹跟踪控制器进行设计，为整个爬壁机器人运动控制器搭建可靠的控制框架，以及后续的动力学建模提供协助速度参考，首先建立运动学模型。

1 爬壁机器人运动学模型

本文以4轮磁吸附爬壁机器人在石油罐体上作业为例[13]，对控制系统进行设计分析，并验证稳定性。以壁面作为作业面，建立二维平面坐标系如图1所示。

图1 爬壁机器人运动学模型

图1中XOY为作业面坐标系，根据悬吊法，爬壁机器人的质心与几何中心重合记为参考坐标系原点o1， 建立随爬壁机器人一起运动的参考坐标系o1x1y1。 设爬壁机器人的状态为p=[x,y,θ]T， 其也可以视为爬壁机器人本体坐标系OXY在作业面坐标系下的位姿量。

设爬壁机器人的期望跟踪状态为pd=[xd,yd,θd]T， 爬壁机器人在作业面坐标系下的运动速度为v， 角速度为ω， 于是可以得到在本体坐标系中爬壁机器人的速度角速度与作业面坐标系中速度角速度的关系如下

(1)

式中：vX,vY为在爬壁机器人本体下的速度量，进一步可以得到

(2)

式中：可以看出，爬壁机器人控制系统为欠驱动系统[15]，可以爬壁机器人对于位置出动跟踪，角度θ随动跟踪。以此思路，接下来设计爬壁机器人的跟踪控制系统。

2 轨迹跟踪控制系统

根据运动学欠驱动的特点，以位置量主动跟踪，角度量随动跟踪，设计双环反馈控制系统：位置环与角度环，如图2所示。

图2 双闭环系统结构

在位置环，通过设计控制律实现对xd,yd的跟踪，并在位置环中产生的角度跟踪量θd输入到角度控制环，实现对偏航角的跟踪，也就是实现θ的随动，从而可以准确跟踪期望轨迹。下面设计轨迹跟踪控制率。

3 轨迹跟踪控制律设计

根据位姿误差的特点，需要使误差收敛，具有良好的滑动模态特性，所以将位姿误差设为滑模切换面，与Lyapunov函数，根据趋近律约束，利用反步法设计控制律，以保证系统稳定。目前工程上为保证简单可行，采用直接求导滑模面代入稳定函数中，设计控制率，这种方法虽然简单有效，但需要依赖增益的调节使得角度快速跟踪期望，来保证系统稳定，这样就牺牲了速度作为代价，所以本文对此进行改进，通过设计约束条件，系统不依赖控制增益调节就能够准确跟踪与达到稳定。

考虑到位置环控制器为主动跟踪期望轨迹，所以在位置环控制率设计中引入动态全局渐进稳定性定理，在趋近律中采用双曲函数代替一次函数，并需要外环位置控制闭环系统满足Lipchitz条件，根据Lyapunov全局稳定性，进而判断整个系统的收敛性。首先设计位置外环控制率。

3.1 控制律设计

首先引入动态全局渐进稳定双曲函数趋近律状态方程[16]

(3)

其中，α,k>0。

对于式(3)，若满足Lipchitz条件，则系统在奇点η=0处是全局渐近稳定的。

证明：爬壁机器人运动控制系统为连续时间非线性时变系统，则讨论此条件下的Lyapunov意义下的稳定性。

(1)V为正定；

则系统原点平衡状态在原点渐近稳定。

(4)

对式(4)求导得到

(5)

根据上述定理启发，取上述状态量“x”为位置误差，设其满足Lipchitz条件，定义滑模切换面，根据反步法设计控制律，使系统渐近稳定，并实现所有位置状态量有界并跟踪期望轨迹。

定义滑模切换函数为轨迹的偏差量：ex=x-xd,ey=y-yd， 对其求导可得

(6)

(7)

建立好位置误差微分方程之后需要设计合适的控制输入v，作用于位置误差微分方程(6)、方程(7)，最终使得使得ex,ey有界或者趋于0。

为了方便设计控制率，这里令

(8)

则位置误差微分方程转化为

(9)

设计控制率为

(10)

其中，α1>0,k1>0,α2>0,k2>0。

由式(9)、式(10)可得

(11)

(12)

对于式(11)，设存在ex1、ex2， 则由Lipchitz条件定义

(13)

由以上分析可见，双曲函数趋近律可得位置控制系统渐近稳定且ex,ey可以趋近于0。

(14)

将位置控制产生的θd传递给内环控制器，通过设计姿态控制率ω来保证θ跟踪θd。

至此，位置控制率设计完成，由式(8)、式(10)得

(15)

或

(16)

下面需要进行内环姿态控制率的设计来使得θ跟踪θd。

3.2 内环姿态控制率设计

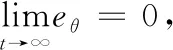
(17)

由于角度跟踪需要快速跟踪期望航向角，以保证爬壁机器人在到达指定位置前首先调整好角度，所以本文根据高为炳院士提出的趋近律设计控制率[18]

(18)

证明：不是一般性，令f(s)=k3s3，s=s3，η=α3， 则

(19)

设Lyapunov函数为

(20)

满足Lyapunov全局渐进稳定性定理条件(1)，对式(20)两边同时求导得

(21)

基于此，利用反步法将式(17)代入式(19)可得控内环控制率为

(22)

式中：k3为常数且大于0；α3表示切换函数s3趋近于0的速率，反映着纠偏能力的强弱，其为常数且大于0。在设计时，不能将α3调的过大，这样容易造成抖动。

至此，姿态控制率设计完成，综上述各式，系统的控制律为

(23)

3.3 闭环系统稳定性分析

根据式(13)的分析可得外环系统满足Lipchitz条件，所以，对于有界控制率输入v或者u1、u2，可保证xe、ye在有限时间内有界并收敛。基于此条件下，可对双闭环系统的全局渐进稳定性进行验证。

设双闭环系统的Lyapunov函数为

(24)

式中：α1>0，α2>0，k1>0，k2>0。

由式(24)可知，Lyapunov函数V满足全局渐进稳定判据(1)(2)，求V的一阶导数得

(25)

考虑到航向角误差的影响，不能将式(11)、式(12)直接代入。对式(2)中各状态量做如下变换

(26)

在位置控制率设计时以θ随动控制，所以替换上式中vcosθd与vsinθd为u1、u2并代入，于是可得到位置误差状态方程如下

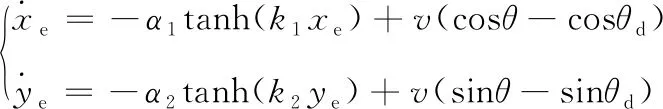
(27)

为简化计算，令α1tanh(k1xe)=t1，v(cosθ-cosθd)=t2，α2tanh(k2ye)=t3，v(sinθ-sinθd)=t4代入式(27)，再代入式(25)，得

(28)

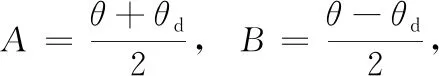
(29)

(30)

根据三角函数不等式的性质 |sinx|≤x， 则式(29)、式(30)可变换为

(31)

(32)

因为θe指数收敛，所以 |cosθ-cosθd|、 |sinθ-sinθd| 均指数收敛，所以由式(31)、式(32)可得

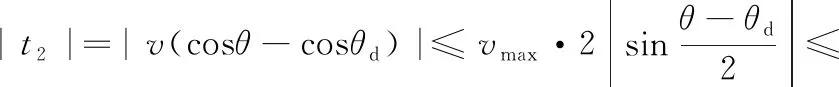
(33)

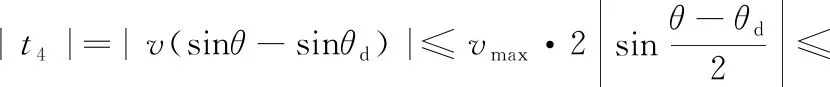
(34)

所以，可以判断

(35)

所以可得

(36)

所以可得

(37)

至此，位置控制器与姿态控制器设计完成并已证明运动学跟踪控制器双闭环系统的全局渐进稳定性。下面通过仿真来验证所设计的算法的可靠性与高效性。

4 仿真验证

将爬壁机器人的作业环境设为大型油罐体表面，其自身重量设为105 kg，轮部半径较小设为0.05 m，以直线跟踪为参考，调整路径跟踪控制器参数见表1。

表1 路径跟踪控制器参数

以直线路径作为参照，取参考起始位置[xd(0)yd(0)θd(0)]=[0 0 0]， 取爬壁机器人的起始位置 [x(0)y(0)θ(0)]=[-6 5 0]， 令xd=t，yd=xd。 与未改进的位置滑模趋近律作比较，如图3～图5所示。

图3中图(a)为一次线性函数趋近律跟踪直线仿真图；图(b)为双曲函数趋近律跟踪直线仿真图。从图中可以得出，相比一次线性函数趋近律，改进后的趋近律可以响应速度较快，并用较短的时间内跟踪直线轨迹，且跟踪过程平稳，所以双曲函数趋近律可以大幅提高爬壁机器人的响应速度，提高控制精度。

图3 直线跟踪仿真

图4中图(a)为一次线性函数趋近律实现对x、y以及θ的跟踪仿真图；图(b)中是双曲函数趋近律对x、y以及θ的跟踪仿真。图4(a)中现实，xd在一次线性趋近律的收敛时间需要7 s，而改进后的趋近律2 s收敛；yd在一次线性趋近律收敛时长同样也需要7 s，但双曲函数趋近律收敛时间仅需要3 s；偏航角的θ的跟踪由于是随动跟踪，收敛时间相差较小。所以，改进后的双曲趋近律比目前使用的一次线性趋近律有着明显的性能提升，对于现场需要紧急救援等工作起到了关键作用。

图4 位置、角度的跟踪

图5 控制输入信号v和ω

如图5中所示，爬壁机器人刚开始的位置即初始状态和初始期望位置存在误差，所以仿真曲线波动明显，然后逐渐趋于稳定，相较于未改进的滑模控制算法图(a)，基于全局稳定的双环滑模控制图(b)的v和ω能够在更短时间内达到期望状态并且波动较小，系统控制输入量ω稳定速度相当，但v在5 s后基本保持不变，而未改进的滑模控制算法则需要10 s左右，改进后控制更加稳定。

综上仿真分析，本文利用改进的双曲趋近律设计的滑模控制律可有效提升爬壁机器人的响应，对于现场一些特殊紧集情况的使用具有较好的效果。

5 结束语

针对爬壁机器人路径跟踪控制，考虑到爬壁机器人快速跟踪预定轨迹，本文改进了以便趋近律提出双曲函数趋近律，结合Lyapunov稳定性利用反步法设计控制律，主要包含以下找工作：

(1)基于作业面坐标系与爬壁机器人本体坐标系，建立运动学方程；

(2)为保证对轨迹跟踪的精度，设计了双环轨迹跟踪控制系统工作图；

(3)根据控制系统结构，为解决依赖控制增益保证系统内部稳定的难题，本文提出用双曲函数趋近律代替一次函数的方法，验证了双曲函数趋近律稳定性的基础上，对位置内环控制率进行设计，提高了位置跟踪的准确性与快速性；为保证航向角能先于位置收敛以保证跟踪精度，采用高为炳教授提出的趋近律设计角速度控制率。对整个双环控制系统进行稳定性分析，结果满足Lyapunov全局渐进稳定，并保证了误差的收敛性；

(4)对改进的基于全局渐近稳定的双环跟踪滑模控制算法与未改进的双环滑模控制算法进行了比较仿真，改进后的控制律跟踪效更好，能很快纠正系统误差，响应速度更快更准确，有效提升爬壁机器人对路径的准确性与快速性。

综上，基于运动学的控制律设计为爬壁机器人的动力学建模及设计控制器做好了准备，搭好了整个运动控制系统的设计框架，下面只需要根据动力学模型将输出力矩的控制参数追踪本文设计的v,ω以实现追踪。