不同载荷作用下滚动轴承应力与变形分析*

□ 王胜曼 □ 唐宇恒

1.保定理工学院 工程技术学院 河北保定 0710002.河北省地矿局第一地质大队 河北邯郸 056000

1 分析背景

滚动轴承是机械传动系统中重要的零部件,安装在变速箱体中对轴起支承作用，并提高轴的旋转精度。轴承性能的好坏及轴承在工作中的受力状态,会直接影响轴承的旋转精度和使用寿命。

在经典机械设计中,学者们认为滚动轴承在径向载荷作用下,位于轴承上半圈的滚动体不受载荷,位于轴承下半圈的滚动体受到载荷，在内外圈与滚动体的接触处,共同产生局部接触变形,变形量与滚动体在轴承中所处的位置有关[1]。近年来,一些学者为了延长滚动轴承的工作寿命,在外力作用下对滚动轴承部件的应力和应变进行了研究。郑煜等[2]采用有限元分析方法,将滚动轴承的接触状态转化为非线性接触问题,求解不同载荷下轴承各部件的接触状态，并给出应力分布规律。岳亮[3]以ANSYS软件为有限元仿真工具,以滚动轴承为例,分析研究了轴承内部应力与载荷的分布规律。姚灿江等[4]应用有限元法分析轴承工作过程中的接触应力,给出了应力分布情况。文献[5-7]应用ANSYS软件对滚动轴承接触应力进行分析,计算出滚动轴承的最大应力和应变,并与传统理论计算所得结论进行比较。学者们使用有限元研究方法，基于不同的研究理论,对不同规格型号的滚动轴承进行了应力和应变分析,但是研究结论局限在滚动轴承的整体变形和应力状态上,对于滚动体局部变形状态,包括变形区域的应力分布、变形区域大小，以及轴承各部件之间应力和变形的分布规律,尚未进行深入研究。

笔者应用Unigraphics NX软件对6207滚动轴承进行三维建模，给定具体边界条件,采用有限元法进行静态数值分析,研究轴承内外圈及滚动体在不同径向载荷作用下的应力和变形情况,为轴承旋转精度和工作寿命的分析与研究提供理论参考。

2 滚动轴承建模

2.1 几何参数

6207滚动轴承的几何参数见表1。

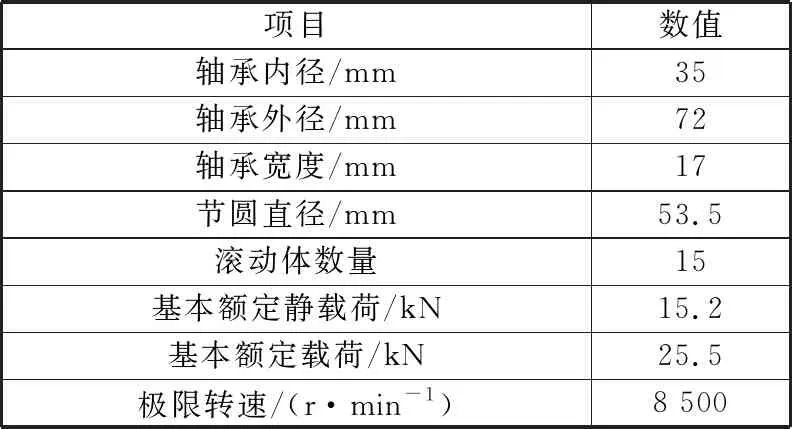
表1 6207滚动轴承几何参数

2.2 材料特性

滚动轴承一般在高速和重载环境下工作,材料通常采用高碳铬轴承钢。笔者将GCr15SiMn高碳铬轴承钢作为滚动轴承材料，材料特性参数见表2。

表2 GCr15SiMn高碳铬轴承钢特性参数

2.3 网格划分

笔者应用Unigraphics NX软件建立滚动轴承三维模型。在高级仿真环境下,设置材料属性,采用自由网格划分,单元总数量为38 124,节点总数量为64 332,建立滚动体与内外圈滚道接触对30个。在轴承上分别施加5 kN、10 kN、15 kN、20 kN径向载荷,在轴承内圈两端面上施加固定约束。滚动轴承有限元模型如图1所示。

▲图1 滚动轴承有限元模型

3 仿真结果分析

3.1 应力

滚动轴承在径向载荷作用下,轴承内圈、外圈，以及不同位置的滚动体会发生不同程度的变形,每个部件上均有不同大小的应力产生。当滚动轴承上施加的径向载荷为5 kN时,轴承应力云图如图2所示。

▲图2 径向载荷5 kN时滚动轴承应力云图

滚动轴承滚动体的编号为1～15，如图3所示。当滚动轴承上施加的径向载荷分别为5 kN、10 kN、15 kN、20 kN时,轴承内圈、外圈和1号滚动体上的最大应力值见表3。

▲图3 滚动轴承滚动体编号

表3 滚动轴承部件最大应力值

根据表3中的数据生成不同径向载荷作用下滚动轴承部件的最大应力曲线,如图4所示。

由图4可以看出,在相同径向载荷作用下,轴承内圈上的应力最大,其次是1号滚动体上的应力,轴承外圈上的应力最小;在不同径向载荷作用下,轴承内圈、1号滚动体和轴承外圈上的应力随载荷增大呈线性增大趋势;随着载荷的增大,轴承内圈应力增大速度最快,滚动体次之,轴承外圈应力增大速度最慢。

将1号至8号滚动体作为研究对象,1号滚动体位于承载区的正下方,8号滚动体位于非承载区的正上方,1号、2号、3号、4号滚动体位于承载区,6号、7号、8号滚动体位于非承载区,5号滚动体位于承载区和非承载区的分界点。1号至8号滚动体在不同径向载荷作用下的最大应力值见表4。根据表4中的数据生成不同径向载荷作用下各滚动体的最大应力曲线,如图5所示。

▲图4 滚动轴承部件最大应力曲线

表4 滚动体最大应力值

▲图5 滚动体最大应力曲线

由图5可以得出,1号滚动体上的应力最大,其次是2号滚动体、3号滚动体,依次类推,8号滚动体上的应力最小,这说明滚动体上应力的大小与滚动体所处的位置有关。在同一载荷作用下,1号至8号滚动体上的应力为脉动循环变应力[8]。在不同径向载荷作用下,不同滚动体上的应力不同。径向载荷越小,滚动体上的应力越小。反之,径向载荷越大,滚动体上的应力也越大。同一滚动体上不同载荷作用下应力的差值与载荷差值成正比关系。

3.2 变形

在不同径向载荷作用下,滚动轴承部件上会出现不同程度的弹性变形。在不同径向载荷作用下,滚动轴承各部件的最大变形量见表5。根据表5中的数据生成不同径向载荷作用下滚动轴承各部件最大变形量曲线,如图6所示。由图6可以得出，载荷相同的情况下,轴承内圈的弹性变形量最大,滚动体的弹性变形量居中,轴承外圈的弹性变形量最小。同一部件在不同载荷作用下,变形量不同。如轴承内圈在5 kN、10 kN、15 kN、20 kN径向载荷作用下,最大变形量依次为7.158×10-4mm、14.32 ×10-4mm、21.47×10-4mm、28.63×10-4mm。轴承内圈、滚动体、轴承外圈的最大变形量与所承受的径向载荷大小成正比关系。轴承内圈与滚动体的最大变形量之差随径向载荷的变化而变化,径向载荷为5 kN、10 kN、15 kN、20 kN时,差值依次为1.071×10-4mm、2.15×10-4mm、3.21×10-4mm、4.28×10-4mm,可见随着径向载荷的增大,这一差值也在增大,说明轴承内圈变形量曲线的斜率与滚动体变形量曲线不同。同理,滚动体与轴承外圈最大变形量之差也随径向载荷的变化而变化,径向载荷为5 kN、10 kN、15 kN、20 kN时,差值依次为0.506×10-4mm、1.01×10-4mm、1.52×10-4mm、2.02×10-4mm,可见随着径向载荷的增大,这一差值也在增大,说明滚动体变形量曲线的斜率与轴承外圈变形量曲线也不同。综合而言,滚动轴承部件的变形量随径向载荷的变化而变化的快慢程度不同,三条最大变形量曲线呈发射状。

表5 滚动轴承部件最大变形量

1号至8号滚动体在不同径向载荷作用下的最大变形量见表6。根据表6中的数据生成不同径向载荷作用下各滚动体最大变形量曲线,如图7所示。

表6 滚动体最大变形量

▲图6 滚动轴承部件最大变形量曲线

1号至5号滚动体在5 kN径向载荷作用下的变形情况如图8所示。

由图7和图8可以看出，在同一载荷作用下,滚动体在轴承中所处的位置不同,滚动体的变形量也不同;1号、2号、3号、4号滚动体处于承载区,变形量较大;5号滚动体处于承载区和非承载区分界处,变形量较处于承载区的滚动体变形量小；6号、7号、8号滚动体处于非承载区,变形量最小。由图8可以看出,1号和2号滚动体的变形区域近似为椭圆形,长、短半轴之比较大,变形区域较集中;3号、4号滚动体变形区域也近似为椭圆形,但是长、短半轴之比较小;5号滚动体变形区域接近于圆形,变形量较小。

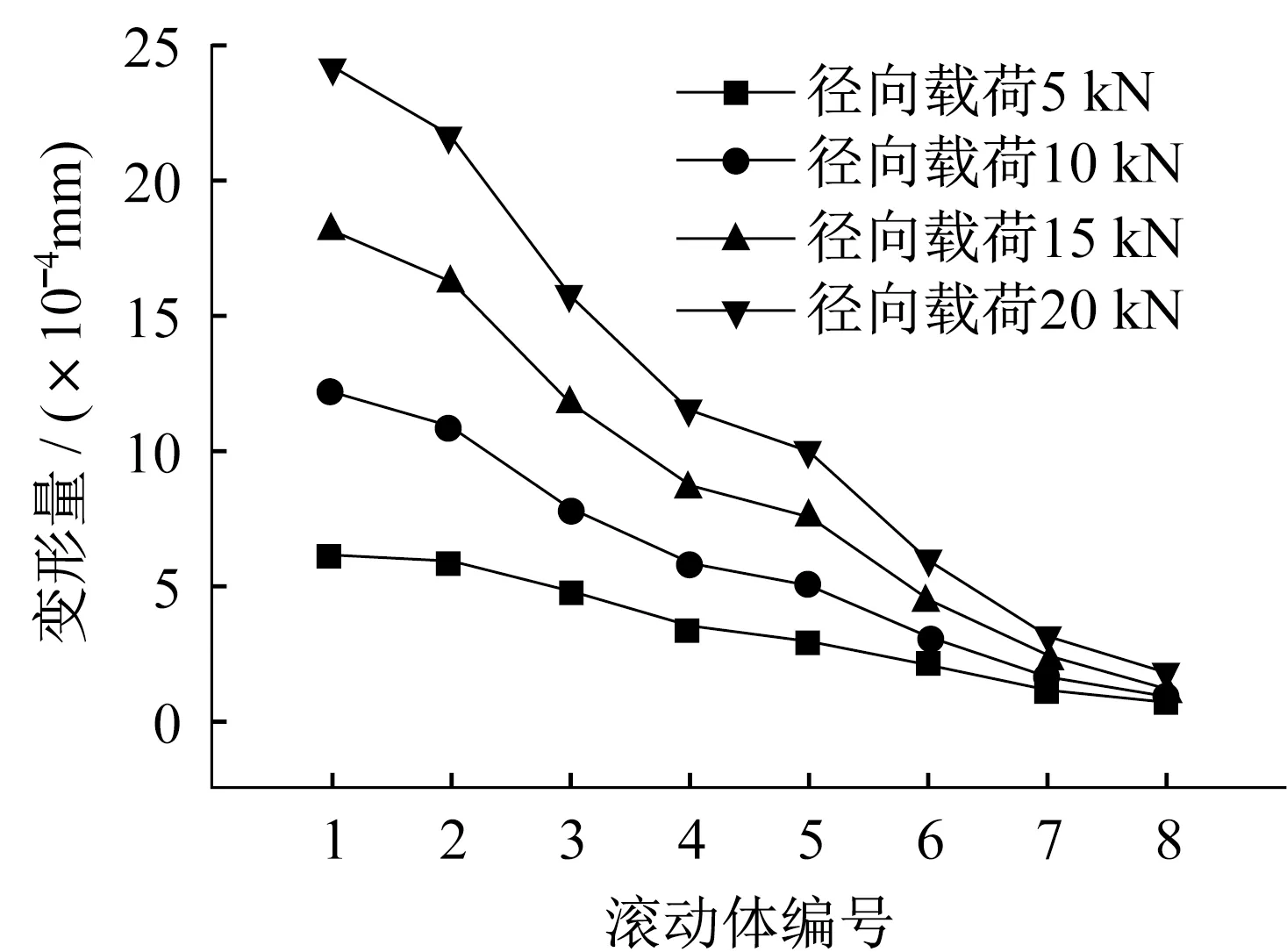
▲图7 滚动体最大变形量曲线

▲图8 径向载荷5 kN时滚动体变形情况

4 结束语

笔者以6207滚动轴承为研究对象,在不同径向载荷作用下,分别对滚动轴承各部件的应力和变形情况进行了仿真分析,得出了结论。在相同载荷作用下，滚动轴承各部件之间的应力、变形逐渐减小。同一部件在相同增量载荷作用下,应力、变形成线性变化。滚动轴承相邻部件应力差值、变形差值随载荷的增大而增大,各部件变形量、应力值曲线斜率各不相同。滚动体应力、变形的大小与滚动体所处的位置有关,承载区滚动体的应力、变形较大,远离承载区的滚动体应力、变形较小。承载区滚动体在径向载荷作用下,变形区域比较集中,长、短半轴之比较大,近似椭圆形。远离承载区的滚动体,长、短半轴之比较小,变形区域接近于圆形,变形量较小。