面向磨机负荷参数预测的多通道机械信号分析评估与优化组合

汤 健, 乔俊飞, 刘 卓, 周晓杰, 余 刚, 赵建军

(1.北京工业大学信息学部, 北京 100124; 2.计算智能与智能系统北京市重点实验室, 北京 100124;3.东北大学流程工业综合自动化国家重点实验室, 沈阳 110004; 4.矿冶过程自动控制技术国家重点实验室,北京 100089; 5.矿冶过程自动控制技术北京市重点实验室, 北京 100089)

在线实时检测与产品质量和生产效率指标密切相关的难测关键过程参数是实现选矿过程运行优化控制的关键因素之一[1-2].数据驱动软测量建模技术广泛用于这些参数的推理估计[3].磨矿过程磨机负荷参数(mill load parameter, MLP)，即料球比(material to ball volume ratio, MBVR)、磨矿浓度(pulp density, PD)和充填率(charge volume ratio, CVR)，决定生产全流程的磨矿生产率.磨机旋转运行产生的机械振动/振声频谱常用于构建MLP预测(MLP forecasting, MLPF)模型[4-6].研究表明，在磨机上不同位置所采集的多源(多通道)机械信号在产生机理、灵敏度和蕴含有价值信息等方面存在差异性、冗余性与互补性，尤其在不同运行工况下更为显著[7-8].

研究表明，机械信号具有显著的非稳态和多组分特性，其特征难以在时域内提取[9-10].通常采用信号处理技术进行预处理以便提取更显著的特征[11-12]，最常用的方法是快速傅里叶变换(fast Fourier transform, FFT)，文献[13]将基于这种方式得到的频谱称为单尺度频谱.理论上，FFT并不适合本文所面对的具有非稳态和多组分特性的机械信号[14].小波分解及其改进算法等时/频分析技术已被广泛用于此类机械信号的故障诊断[15-16]，但仍未实现信号的自适应分解；经验模态分解(empirical mode decomposition, EMD)及其改进算法能够克服上述缺陷，获得具有不同时间尺度且理论上可进行物理解释的系列平稳子信号[17-20].从机械信号产生机理的视角，这些子信号具有不同的产生来源和频率特性；文献[13]将多尺度子信号进行FFT变换后的数据称为多尺度频谱，其已广泛用于设备故障诊断、磨机负荷建模和识别[21-22].虽然理论上多尺度机械频谱能够构建更具合理性解释的MLPF模型，但EMD及其改进算法的复杂分解过程也会产生一些非确定和不准确的信息.因此，基于FFT的单尺度频谱仍是实际工业过程中应用最为广泛的数据.

基于较高频率分辨率的单/多尺度频谱包含的频率变量维数高且相互之间具有较强共线性.潜结构映射或偏最小二乘(partial least square, PLS)算法及核偏最小二乘(kernel PLS, KPLS)算法能够提取低维潜在变量(latent variable，LV)构建回归模型，适合对高维频谱数据建模[23].为提高MLPF模型泛化性能，文献[24]提出基于操作输入特征与采样训练样本的双重维度集成构造策略，用以构建选择性集成(selective ensemble, SEN)MLPF模型，该方法构建的软测量模型能够有效融合多源有价值信息，与运行专家智能感知磨机负荷的机制相类似，但所构建的MLPF模型结构较为复杂；此外，面对小样本时，基于单尺度频谱的MLPF模型的泛化性能较好，但在模型可解释性和洞悉研磨过程机理等方面存在欠缺.为克服工况漂移带来的泛化性能下降问题，文献[25]和文献[26-27]分别构建了基于样本更新和迁移学习的MLPF模型，但仍未解决如何自适应选择多运行工况下更有价值的多通道机械信号的问题.

上述研究表明，面向球磨机筒体振动、轴承座振动和振声信号等多源(多通道)机械信号，如何度量这些不同通道信号对构建MLPF模型的贡献率、如何识别存在测量偏差的通道信号、如何对更有价值的通道信号进行互补融合等方面的研究却鲜有报道.也就是说，需要一种新的策略用于辅助判断哪些信号(通道)更加稳定、哪些信号更适应实际需求、哪些信号能够互补，以适应多种运行工况，进而提高MLPF模型的泛化性能.

针对上述问题，本文提出了面向MLPF预测的多运行工况多通道机械信号分析评估与优化组合方法.首先，将多源机械振动和振声信号变换至频域获得高维频谱数据；接着，依据先验知识将其划分为多种运行工况并分别构建基于传统单模型结构的MLPF模型，基于验证数据获得模型的预测误差和结构参数；然后，通过标准化后的验证误差和结构参数度量模型预测性能和蕴含信息贡献率，通过新定义综合评估指标对多通道机械信号进行分析评估，并基于设定阈值完成通道初选；最后，通过组合优化获得具有最佳预测性能的MLPF模型.通过实验球磨机的多通道机械信号仿真验证了所提方法的有效性.

1 磨矿过程与多通道机械信号

磨矿过程通常采用两段式闭式磨矿回路(grinding circuit, GC)，其一段磨矿回路(GC I)的工艺流程和多源机械信号的检测位置如图1所示.

首先，新给矿从矿仓进入预选机并排出尾矿，同时伴随着新加水和周期性添加的钢球；接着，与来自水力旋流器的沉砂混合后进入球磨机，通过钢球与矿石间的周期性冲击和研磨作用对矿石进行破碎，形成矿浆后依靠其流动排出磨机并进入泵池；对泵池新加水并对矿浆进行稀释，再将其泵入水力旋流器进行筛选：矿石粒度较细的溢流进入二段磨矿回路(GC Ⅱ)，较粗的进入球磨机再磨.

工业实际表明，球磨机是整个磨矿过程的瓶颈设备.通常，磨矿过程的最大化生产率通过最优化磨矿回路循环负荷的控制策略予以实现，后者由磨机负荷决定.在实际工业过程中，磨机内部任何一种负荷参数的异常均会导致磨机过负荷或者欠负荷，进而导致生产过程中断甚至磨矿设备损坏.因此，磨机负荷参数是磨矿过程中与生产过程安全、质量和效率均直接相关的难以检测参数.磨机负荷及其状态、磨机负荷参数间的关系详见文献[28].

球磨机是依靠钢球和矿石负荷间的冲击和研磨作用进行矿石破碎的重型旋转设备.磨机系统不同位置机械信号的产生机理示意图如图2所示.

综上可知，球磨机系统不同位置所测量的多源机械信号所蕴含的MLP信息具有冗余性和互补性.此外，不同工业现场对传感器的安装要求也存在差异性，所测量信号也可能因安装方式不同而存在测量偏差，某些通道在使用中甚至会出现故障信号.因此，有必要对多源(多通道)机械信号进行分析评估和优化组合以提高MLPF模型的泛化性能.

2 多源机械信号分析评估与优化组合

2.1 机械频谱变换

(1)

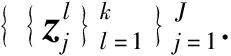
(2)

2.2 通道贡献率度量

将上述建模样本划分为建模和验证数据两部分，以第i种工况为例，其过程为

(3)

式中：k=ktrain+kvalid;ktrain和kvalid分别为训练和验证数据集的样本数量.

(4)

(5)

(6)

(7)

计算.进一步，本文新定义综合评估指标λji用于评估第i种工况下第j个通道的机械信号

(8)

式中：0≤α≤1，α能够在预测性能贡献率和蕴含信息贡献率之间进行均衡；较小的λji值表示该通道机械信号具有较佳综合指标.

考虑到全部I种运行工况，对第j个通道的综合分析评估值λj采用

(9)

计算.式中wji表示第i种运行工况下第j个通道的加权系数，且

(10)

由此可知，α=0时仅考虑蕴含信息贡献率，α=1时仅考虑预测性能息贡献率，故α可依据工业过程实际需求进行选择，在预测性能与蕴含信息贡献率间进行均衡.显然，λj能够为在不同工况下综合评判通道信号质量和构建MLPF模型提供量化依据.

最佳通道机械信号的综合评估指标值λBest通过优选得到，即

λBest=Min(λ1,…,λj，…,λJ)

(11)

式中，Min(·)表示获取最小值的函数.

基于式(11)的准则，将全部机械通道按照综合评估指标值由小到大进行排序，并重新标记为

(12)

式中：λ1*≥λj*≥λJ*；J*=J；λj*表示排序后的第j*个通道的综合评估指标值.

进一步，通过设定阈值λthresh进行通道信号初选

(13)

式中∅表示空集.

基于上述准则，将初选通道数量记为Jsel，其综合评估指标值集合记为

(14)

式中：Jsel≤J；1≤jsel≤Jsel表示经初选得到的第jsel个通道.

2.3 通道优化组合

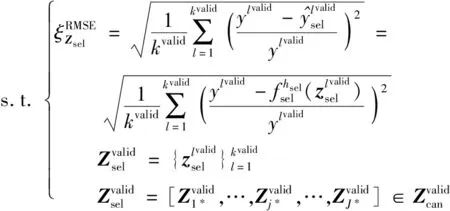
(15)

(16)

通过上述过程，实现了I种运行工况下J个通道机械信号的分析评估和优化组合.

3 应用验证

3.1 实验描述

本实验在旋转速度42 r/min、直径602 mm和长度715 mm的小型实验磨机上进行，所采用钢球直径为30 mm、铁矿粉直径小于2 mm.全部8个通道机械信号的采样频率均为51.2 kHz，传感器安装位置和类型分别为：固定在磨机筒体表面的 2个加速度传感器、与磨机筒体表面相距2 mm的2个声传感器、位于磨机轴承座左侧测量垂直振动、位于右侧测量垂直和水平振动的3个加速度传感器和位于磨机研磨区域下方10 mm的1个声传感器.这些通道依次被标记为Ch1～Ch8，如图3所示.

实验采用固定钢球和水负荷逐渐增加矿石负荷的方式共进行了139次实验，即共139个样本，其中4/5用于训练和验证集，其余用于测试集.

3.2 机械频谱结果

首先对时域信号进行滤波处理，然后将磨机运行稳定、旋转整周期的数据转换至频域得到多个周期的频谱，最后将这些谱数据进行平均得到最终建模数据.

考虑到磨机启动和停止阶段所测量机械信号非平稳性的影响，去掉磨机运行前8圈和后5圈的数据.每次处理的长度为磨机旋转一周的数据，窗函数采用参数为1 024的汉明窗，数据重叠长度为512.在钢球负荷292 kg、水负荷35 kg和矿石负荷25.5 kg的实验工况下，8个通道的机械频谱如图4所示.

图4表明，不同通道的机械信号频谱存在差异性：Ch1和Ch2具有单峰特性；Ch3具有双峰特性；Ch4在低频段具有较高能量(与传感器布设方式和工作状态相关)；Ch5、Ch6和Ch7具有多峰特性且模态分布存在差异(存在与实验设备相关的多个振动模态)；Ch8的低频能量较高并体现出半峰特性.因此，选择合适位置的可靠多源信号构建MLPF模型是非常必要的.

3.3 贡献率度量结果

本文采用适合高维共线性数据建模的PLS算法构建MLPF模型，并且将实验数据认定为一种工况.以MBVR为例，基于验证数据集的模型复杂度数量n和预测性能RMSRE间的相互关系如图5所示.

由图5可知，基于不同通道机械信号频谱所构建的MBVR模型的复杂度间存在差异性，所蕴含的信息也不同.面向不同数据集的MLPF模型的统计结果详见表1.

表1表明：

表1 基于不同通道机械信号的MLPF模型的预测结果

1)针对MBVR，训练、验证和测试数据集的最小RMSRE分别为0.009 04、0.034 54和0.031 95，分别源于Ch3、Ch6和Ch6；Ch3为筒体表面振声，表明该通道可采集更多有价值信息，其LV数量为19，高于其他通道，也表明其蕴含的信息较分散；Ch6为靠近电机侧的轴承座垂直振动，在LV数量和预测性能间达到了较好的均衡.

2)针对PD，训练、验证和测试数据集的最小误差RMSRE分别为0.001 93、0.009 12和0.014 84，分别源于Ch1、Ch1和Ch4；Ch1为筒体表面振动，Ch4为筒体近表面振声，表明该信号蕴含PD信息较多；同时，Ch1的LV数量较大也表明了其蕴含信息较其他通道更为分散，这与其灵敏度高相关；此外，Ch4在LV数量和预测性能间达到了较好的均衡.

3)针对CVR，训练、验证和测试数据集的最小误差RMSRE分别为0.003 54、0.009 23和0.008 29，分别源于Ch3、Ch6和Ch6；Ch3为筒体近表面振声，表明其蕴含的CVR信息较丰富，但其LV数量较大，也表明了蕴含信息较为分散；作为轴承座右侧垂直振动的Ch6在LV数量和预测性能间达到了较好的均衡.

4)针对3个不同磨机负荷参数，MBVR和CVR基于Ch6、PD基于Ch4具有最佳预测性能.因此，不同MLP对不同通道机械信号的灵敏程度具有差异性，这与之前的研究相符合.

依据本文所提方法计算预测性能和蕴含信息贡献率，分别设定α=0.2、0.5和0.8，计算综合评估指标的统计结果如表2所示.

表2 针对3个MLPF模型的机械通道综合评估指标统计结果

表2表明:α=0.5和0.8时，筒体表面振声Ch4对MBVR和CVR具有最小λj值；当α=0.5和0.8时，轴承座右侧垂直振动Ch6针对3个MLP均具有最小值.

全部机械通道针对不同MLP的综合评估指标分布曲线如图6所示.

由图6可知：随着α值的增大，Ch1的综合评估指标值降低，即分配给预测性能的权重越大，则Ch1的贡献率越大，这与Ch1是具有高灵敏度的筒体振动信号相关；但对于Ch2，结果却相反，表明Ch2的测量位置或固定方式不是很理想，该通道在后续建模中应予以剔除；此外，Ch4比Ch3更稳定，Ch6比Ch5和Ch7更可靠；Ch8为通常采集的磨机研磨区域下方的振声信号，与其他通道相比较，其综合评估指标值为平均水平.

因此，从多通道机械信号产生机理的角度和上述定量的分析结果可知，这些经综合评估后所确定的较为可靠的信号间也存在互补性，需进行优化组合.

3.4 优化组合结果

此处，对α=0.2、0.5和0.8时的通道组合情况分别进行讨论.

1)α=0.2

将阈值λthresh设定为0.1，为PD、MBVR和CVR初选的通道均为Ch2、Ch4和Ch6.采用枚举方式进行通道组合.以PD为例，预设不同通道数量MLPF模型的预测性能统计结果如表3所示.

表3 α=0.2时基于不同预设通道数的MLPF模型(PD)的预测结果

在α=0.2时，综合评估指标主要偏向于模型结构复杂度.由表3可知，与最佳通道Ch6相比较，最佳测试性能通道组合{Ch2,Ch4,Ch6}在训练、验证和测试数据集的预测性能上均得到提高，其对应RMSRE分别为0.003 68、0.010 55和0.011 20，相应地分别提高了163.70%、22.94%和41.70%，输入变量维数增加了3倍，表征模型结构复杂度的LV数量增加了1倍多；与通道{Ch4,Ch6}相比，其LV数量为8，与单通道相差不大，测试性能提高了24.86%.

2)α=0.5

将阈值λthresh定为0.1，PD初选通道为Ch4、Ch6和Ch8，MBVR和CVR初选通道为Ch4和Ch6.仍以PD为例，预设不同通道数量的MLPF模型预测性能的统计结果如表4所示.

表4 α=0.5时基于不同预设通道数的MLPF模型(PD)的预测结果

在α=0.5时，综合评估指标在预测性能和模型结构复杂度间取得相同的均衡.由表4可知，与最佳通道Ch6相比较，不同的通道组合在训练、验证和测试数据集的预测性能上均得到提升；以最佳测试性能通道{Ch4,Ch8}为例，其对应的RMSRE分别为0.003 65、0.012 60和0.009 73，相应地分别提高了166.40%、2.94%和63.09%，输入变量维数增加了2倍，表征模型结构复杂度的LV数量增加了1倍多；通道{Ch4,Ch6,Ch8}与Ch6相比，在训练性能上的提升最大.

3)α=0.8

将阈值λthresh定为0.09，3个MLP所初选的通道均包含Ch1、Ch4和Ch6，PD还包含Ch8.仍以PD为例，预设不同通道数量的MLPF模型预测性能的统计结果如表5所示.

在α=0.8时，综合评估指标主要偏向于模型预测性能，这是多数工业过程的实际需求.由表5可知，与最佳通道Ch6相比较，最佳综合评价指标通道组合{Ch1,Ch4,Ch6}在训练、验证和测试数据集的预测性能上均得到提高，其对应的RMSRE分别为0.008 04、0.010 38和0.008 05，分别提高了20.78%、24.95%和97.09%，输入变量维数虽增加了3倍，表征模型复杂度的LV数量只增加了1个；通道组合{Ch1,Ch6}和{Ch1,Ch4,Ch8}在训练数据集上则明显存在过拟合，但通道组合{Ch1,Ch6}的测试性能与最佳组合{Ch1,Ch4,Ch6}的性能相差较小，表明Ch1在预测精度上更为重要.

表5 α=0.8时基于不同预设通道数的MLPF模型(PD)的预测结果

从上述过程可知，α=0.2，0.5和0.8时，最佳测试误差分别为0.011 20、0.009 73和0.008 05，结构复杂度参数为13、13和8，与最佳单通道Ch6(测试误差为0.015 87，结构复杂度为7)相比，结果表明：通道组合是非常必要的，通道信号间的互补特性能够显著提高模型预测性能和降低模型结构复杂度.

4 结论

1)基于多运行工况多源(多通道)机械信号构建的磨机负荷参数预测模型能够为实现磨矿过程优化运行与控制提供支撑.本文重点关注如何选择多运行工况下的多通道机械信号及如何优化组合有价值多通道信号构建具有最佳预测性能的软测量模型.本文所提出的综合评估指标能够有效地度量和均衡多通道机械信号预测性能和蕴含信息贡献率，结合设定阈值能够选择产生机理互补和测量数据可靠的多通道机械信号进行组合，能够有效排除冗余和测量存在偏差的通道.通过实验球磨机的多通道机械信号仿真验证了所提方法的有效性.

2)需要明确的是，上述结果是采用线性潜结构模型面向实验球磨机系统进行多通道机械信号的分析，其结论在工业磨机上的适应性待验证.更进一步的研究也需要结合多运行工况和多组分信号自适应分解算法进行深入.在工业实际上，需要依据多通道信号间预测性能的相似性及经济性指标选择具有较高性价比的通道进行优化组合.此外，多通道频谱数据组合后造成模型输入维数增加，有待于研究维数约简策略和选择性信息融合机制予以克服.