基于相关向量机的煤自燃预测方法

刘宝， 穆坤， 叶飞， 汪帆， 王静婷

(1.西安科技大学 电气与控制工程学院， 陕西 西安 710054；2.西安翻译学院 工程技术学院， 陕西 西安 710105)

0 引言

煤自燃不仅给煤矿生产带来极大不便，一旦发生爆炸，还会对矿工的生命安全造成极大威胁[1-2]。煤自燃的有效预防是煤矿安全生产的关键，对煤自燃程度的准确预测是煤自燃预防的前提。煤自燃过程中，指标气体浓度会随煤质氧化的程度发生变化，因此，可通过检测及分析该过程中指标气体浓度来预测煤自燃温度，达到预测煤自燃程度的目的[3-5]。

近年来，学者们通过各种机器学习算法对指标气体浓度与煤自燃温度的关系展开了研究。文献[6]通过径向基(Radial Basis Function, RBF)神经网络学习方法研究了气体浓度与煤自燃温度之间的关系。文献[7]通过支持向量机(Support Vector Machine, SVM)的改进算法对煤自燃温度进行预测。RBF神经网络方法用于预测煤自燃具有非线性映射能力与泛化能力强的优点，然而易陷入局部最优，网络结构复杂；SVM虽可避免“维数灾难”，适用于小样本数据集，但核函数受Mercer条件的限制，对参数的选择敏感[8]；传统的机器学习算法对煤自燃温度进行预测时存在较大误差。

针对上述问题，本文结合贝叶斯、极大似然估计等理论，提出了基于相关向量机[9-10](Relevance Vector Machine，RVM)的煤自燃程度预测方法，根据特征气体浓度准确地对煤自燃温度进行预测。

1 RVM回归

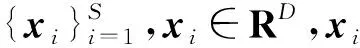
ti=y(w,xi)+εi

(1)

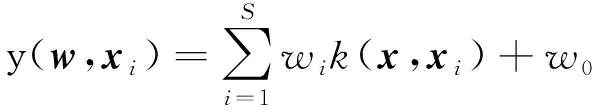
(2)

式中：y(w,xi)为由权值决定的输出值；w为S+1维权值wj组成的向量，j=0,1,…,S，即w=[w0,w1,…,wj,…,wS]T；x是由xi组成的矩阵，即x=[x1,x2,…,xi,…,xS]T；εi为第i个噪声误差，εi～N(0,δ2)，N(·)为高斯分布，δ2为高斯噪声的方差；k(x,xi)为核函数k(xn,xi)组成的核向量，即k(x,xi)=[k(x1,xi),k(x2,xi),…,k(xi,xi),…,k(xS,xi)]，n=1,2,…,S。

当ti相互独立时，训练样本的极大似然函数为

(3)

式中φ为核函数k(xn,xi)组成的核矩阵，即φ=[φ(x1),φ(x2),…,φ(xn),…,φ(xS)]T，φ(xn)=[1,k(xn,x1),k(xn,x2),…,k(xn,xi),…,k(xn,xS)]。

若直接用最大似然法求w与δ2，会产生“过拟合”现象，可对w赋予均值为零、超参数为α的高斯先验分布。

(4)

式中α为S+1维的超参数向量，α=[α0,α1,…,αj,…,αS]T。

由马尔科夫性质知，对于测试输入矩阵x*，其对应预测值y*的概率表达式为

(5)

式中P(w,α,δ2|t)=P(w|t,α,δ2)P(α,δ2|t)。

由于P(α,δ2|t)∝P(t|α,δ2)P(α)P(δ2)，其中“∝”表示成比例，则t的条件分布为

(6)

式中Ω为t的条件分布协方差，Ω=δ2I+φA-1φT，I为单位阵，对角阵A=diag(α0,α1,…,αj,…,αS)。

P(y*|t)等价形式为

(7)

y*=μTφ(x*)

(8)

(9)

式中：μ为w的后验分布均值，μ=δ-2QφTt；φ(x*)为测试样本组成的核矩阵；Q为w的后验分布协方差Q=(δ-2φTφ+A)-1。

2 基于RVM的煤自燃预测方法

基于RVM的煤自燃预测流程如图1所示。

图1 基于RVM的煤自燃预测流程Fig.1 Prediction process of coal spontaneous combustion based on RVM

(1) 采集气体浓度与煤自燃温度。建立训练集(x,t)和测试集(x*,y*)，其中x和x*分别为训练集和测试集的输入矩阵，输入数据集合元素属性包括C(O2)，C(N2)，C(CO)，C(CO2)，C(CH4)和O(CO/CO2)，其中C(·)为气体浓度，O(a/b)为a，b两种气体浓度之比，Vmax为煤自燃预测温度，包括训练集的测量温度t和测试集的预测温度y*两部分。

(2) 对训练集的输入向量xi构造高斯核函数

(10)

式中：λ为高斯核宽度；xn与xi分别表示训练集中第n组和第i组输入向量。

构造核函数的目的是将训练集的输入矩阵x由低维空间映射到高维空间，以获得更好的训练效果。

(3) 初始化超参数α与噪声方差δ2，对α和δ2进行迭代。

(11)

(12)

(4) 达到迭代终止条件后，部分αj会趋于无穷大，对应的wi为0；其余的αj趋于有限值，对应的输入向量xj被称为相关向量。完成训练后，得到最佳的w和δ2。

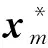
(13)

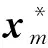
(6) 将测试集数据和测试核矩阵代入由训练集确定的最优w和δ2的RVM模型中，即可得到煤自燃温度的预测值y*和预测方差δ*2。

3 现场实验

通过模拟煤自燃实验，验证基于RVM的煤自燃预测方法的可行性与准确性。

3.1 煤自燃数据获取

陕西省长武县亭南煤矿采用综采放顶煤采煤工艺，在通风不良的环境下易发生煤自燃现象。为了有效预防煤自燃灾害的发生，创造与亭南煤矿相似的供氧与蓄热条件，检测该过程中煤自燃温度与指标气体浓度的变化。

利用XK型煤自燃实验平台进行实验，该平台由炉体、气路、控制及检测4个部分组成，如图2所示。炉体主体部分呈圆桶状，最大装煤高度为150 cm，内径为120 cm，总装煤量可达1.5 t；炉体周围的保温层与跟踪外层煤温的控温水层可保证炉内煤体处于良好的蓄热环境，水层中装电热管与进气预热紫铜管，在炉中心轴处设有取气管。炉体顶、底部均有气流缓冲层，使气流均匀通过煤体，空气经控温水层预热，创造与煤自燃温度相同的环境，然后从炉体底部送入。此外，炉内多处布置了测温探头和气体采样点。

图2 煤自燃实验台Fig.2 Coal spontaneous combustion test bench

选用SP3430气相色谱仪对气体进行采集与分析，如图3所示。该气相色谱仪主要由双柱箱、自动取样机、色谱数据处理工作站组成。

图3 SP3430气相色谱仪Fig.3 SP3430 gas chromatograph

通过SP3430气相色谱仪检测特征气体的成分及浓度，亭南煤矿的煤自燃样本数据见表1。选取其中30组样本数据为训练集，剩余8组样本数据为测试集。

表1 亭南煤矿的煤自燃样本数据Table 1 Sample data of coal spontaneous combustion in Tingnan Coal Mine

3.2 模型的构建及验证

构建RBF神经网络、SVM、RVM 3种煤自燃预测模型。模型参数分别设置如下：RBF神经网络模型的扩展速度为371；SVM模型高斯核函数的核宽度为19，正则化系数为4 583；RVM模型核函数的核宽度为579。

基于RVM煤自燃预测模型的实施步骤如下。

(1) 初始化超参数向量α及方差δ2并设置最大迭代次数。

(2) 设置α的最大值，在RVM迭代过程中，当α超过该最大值时，便认为其趋向于无穷大，对应的w为0，则对该部分的值就不再更新；设置方差阈值，当其方差的相对误差小于阈值时，便认为达到训练要求，退出循环。

(3) 本实验训练数据经过323次迭代后，最终达到精度要求，此时有16个αj趋于有限值，wj不为0，得到RVM最优模型参数。

(4) 将测试样本代入已训练的模型中，预测采空区煤自燃温度值，并与测量值进行比较分析。

3.3 结果与讨论

测试集真实温度值与3种方法的预测温度值对比结果如图4所示。基于RVM的煤自燃预测值在实际值附近上下波动，总体预测精度较高；基于SVM的煤自燃预测精度次之；基于RBF的煤自燃预测误差偏大，预测精度不理想。

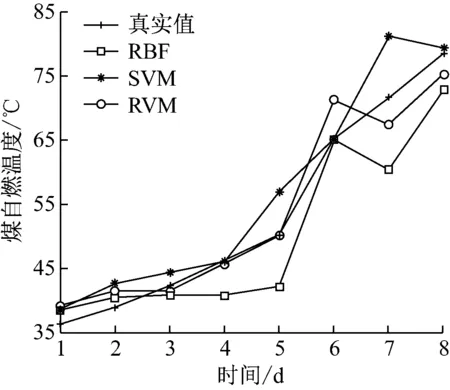
图4 3种方法的预测结果Fig.4 Prediction results of three methods

3种方法的相对误差如图5所示。3种方法的预测相对误差都在20%以内，基于RBF和SVM的煤自燃预测方法各有2个样本相对误差大于10%，基于RVM的煤自燃预测方法相对误差均小于10%，较为集中且相对较小。

图5 3种方法的预测相对误差Fig.5 Prediction relative errors of three methods

3种方法的平均相对误差见表2。在3种煤自燃预测方法中，基于RBF和SVM的煤自燃预测方法训练误差较小，但测试误差较大，说明这2种方法存在严重的“过拟合”现象，泛化能力差。基于RVM的煤自燃预测方法的训练误差与测试误差比较接近且预测精度最高。由此可知，RVM对煤自燃温度预测的效果优于传统的基于RBF和SVM的煤自燃预测方法。

表2 3种方法的平均相对误差Table 2 Average relative errors of three methods

4 结论

通过模拟亭南煤矿煤样自燃过程的环境，检测并记录该过程中特征气体浓度值与煤自燃温度值。结合贝叶斯、极大似然估计等理论构建基于RVM的煤自燃预测模型，并与基于RBF神经网络和SVM的煤自燃预测模型进行比较。结果表明，传统的煤自燃温度预测方法存在“过拟合”现象，而基于RVM的煤自燃预测方法预测精度高，且具有预测误差小、泛化能力强、模型更稀疏等优点，更适合于对煤自燃等复杂非线性问题的预测。