基于灰度共生矩阵与回归分析的矿井水灾感知

曹玉超

(中国矿业大学(北京) 机电与信息工程学院， 北京 100083)

0 引言

水灾为煤矿重特大灾害之一[1]。水灾感知可采用水文钻孔[2-4]、微震监测[5]、水位监测[6]、应力监测、电阻率监测、图像识别[7-10]等方法。水文钻孔施工周期较长，且极易发生孔内事故。微震监测、水位监测、应力监测、电阻率监测等传感器感知方法属于接触式测量，在灾变情况下容易受到破坏，影响稳定性。通过图像识别感知水灾具有非接触、蕴含信息丰富等特点，越来越受到人们关注。文献[7]通过水位标尺图像监测矿井水位，但只能在涌水量达到一定程度后才能感知水灾，时效性较差。文献[8]提出基于图像像素灰度统计值的水灾识别方法，对突涌水直接进行监测，能及时发现水灾，但容易受到井下灯光设备干扰，灯光变化时图像的灰度特征稳定性较差。文献[9]提出基于图像纹理特征的矿井水灾感知方法，虽然解决了光照影响带来的不稳定性，但该方法耗时较长，识别率较低。鉴于此，本文提出了一种基于灰度共生矩阵与回归分析的矿井水灾感知方法，基于灰度共生矩阵提取突涌水、煤、岩石图像纹理特征，通过回归分析对突涌水、煤、岩石图像进行分类，从而识别水灾。

1 方法原理

1.1 灰度共生矩阵

灰度共生矩阵用于图像纹理信息有效提取[11-14]。假设图像分辨率为N×N，则灰度共生矩阵的元素为

p(i,j,δ,θ)={(x,y),(x+dx,y+dy)∈

N×N|f(x,y)=i,f(x+dx,y+dy)=j}

(1)

式中：(x，y)为参考点；(x+dx,y+dy)为偏移点；f(x,y)=i表示参考点的灰度值为i；f(x+dx,y+dy)=j表示偏移点的灰度值为j；δ为偏移点的偏移量；θ为偏移点的偏移角度。

笔者选用灰度共生矩阵的对比度、差异性、齐次性、熵、相关性和能量作为特征值。

(1) 对比度：反映图像纹理沟纹深浅程度和清晰度。对比度越大，表明图像纹理沟纹越深，视觉效果越清晰；对比度越小，表明图像纹理沟纹越浅，视觉效果越模糊。对比度表达式为

(2)

式中L为图像灰度级数。

(2) 差异性：反映图像的局部对比度变换情况。局部对比度增大时，差异性增大；局部对比度减小时，差异性减小。差异性表达式为

(3)

(3) 齐次性：反映图像局部纹理的均匀变化程度。图像局部纹理均匀变化时，灰度共生矩阵的相邻元素变化较慢，齐次性较大；图像局部纹理不均匀变化时，灰度共生矩阵的相邻元素变化较快，齐次性较小。齐次性表达式为

(4)

(4) 熵：反映图像包含的信息量。熵越大，表明图像包含的信息量越大；熵越小，表明图像包含的信息量越小。熵表达式为

(5)

(5) 相关性：反映图像中局部灰度相关性，度量灰度共生矩阵的元素在行或列方向上的相似性。灰度共生矩阵的元素值相差越小，相关性越大；灰度共生矩阵的元素值相差越大，相关性越小。相关性表达式为

(6)

(6) 能量：反映图像灰度分布均匀程度。图像灰度分布越集中，能量越大；图像灰度分布越分散，能量越小。能量表达式为

(7)

1.2 回归分析

将对比度x1、差异性x2、齐次性x3、熵x4、相关性x5、能量x6组成特征向量，纹理图像在由特征向量构成的空间X中有唯一表示，存在非线性回归方程(式(8))使突涌水和煤岩背景分离。

(8)

式中：km为斜率；φ(xm)为低维空间X映射到高维空间Z的核函数；b为截距。

高维空间中存在如下映射关系：

zm=φ(xm)

(9)

式中zm为高维空间的向量分量。

则低维空间的非线性回归方程(式(8))可转换为

(10)

假设煤、岩石与突涌水样本集中各样本的特征向量到非线性回归方程的距离为dvu(v=1，2，3；u=1,2,…,Mv,Mv为每种样本集中样本数量)，各样本集中样本的特征向量到非线性回归方程的最小距离为

dv=min(dv1,dv2,…,dvMv)

(11)

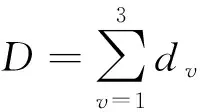
(12)

2 实验分析

为验证本文方法的有效性，使用Intel Core i5、双核CPU主频1.8 GHz、内存8 GB、64位操作系统的计算机进行实验。实验选取井下常见的无烟煤、砂岩各250张图像作为负样本，并与250张突涌水图像组成数据集，图像分辨率为256×256。

2.1 特征值

不同样本图像特征值如图1所示。可看出突涌水的对比度、差异性、齐次性特征值与无烟煤特征值较相似，但熵、相关性、能量特征值与砂岩较相似，仅利用部分特征值很难将突涌水从复杂的煤岩背景中提取，而综合采用对比度、差异性、齐次性、熵、相关性、能量特征值可有效表示突涌水的纹理特征。

图1 不同样本图像特征值Fig.1 Image eigenvalues of different samples

2.2 识别率

在相同实验硬件条件下，文献[9]方法的识别率为81.97%，本文方法识别率明显提高，为96.33%。这是由于相对于文献[9]方法中双树复小波频域变换，灰度共生矩阵对于纹理特征的提取能力较强，能从多个维度对纹理图像的特征进行抽取，且在识别分类时采用回归分析将复杂的多维度向量在特征空间中进行有效表示，相对于单一的统计量建模具有良好的可区分性。

2.3 耗时

本文方法耗时由灰度共生矩阵计算时间与识别时间组成，结果见表1。可看出单张图像灰度共生矩阵计算平均耗时为16.145 6 ms，识别平均耗时为0.142 9 ms，本文方法平均耗时为16.288 5 ms。

文献[9]方法平均耗时为81.933 4 ms，本文方法比文献[9]方法耗时缩短了65.644 9 ms。这是由于文献[9]方法对图像进行双树复小波多级分解时，每个尺度下都需单独计算各方向的滤波系数，双树复小波多级分解的后一级系数需要在前一级分解的基础上计算，属于典型的串行操作，耗时较长；本文方法利用灰度共生矩阵进行纹理特征提取时，对不同的矩阵块可进行并行计算，各并行计算内容之间并无依赖关系，所以耗时大大减少。

表1 基于灰度共生矩阵与回归分析的矿井水灾感知方法耗时Table 1 Time-consuming of mine flood perception method based on gray level co-occurrence matrix and regression analysis ms

3 结语

提出了一种基于灰度共生矩阵与回归分析的矿井水灾识别方法。计算样本图像的灰度共生矩阵，提取灰度共生矩阵的对比度、差异性、齐次性、熵、相关性、能量作为特征值并组成特征向量；以样本图像的特征向量到非线性回归方程的最小距离之和最大为依据确定分类器，通过分类器识别水灾。实验结果表明，对于分辨率为256×256的图像，该方法识别率为96.33%，单张图像平均耗时16.288 5 ms，基本满足井下实时监控需求。