基于能量法的轴横向荷载作用下单桩受力变形分析
2020-09-27陈金海
张 玲,陈金海,欧 强
(湖南大学岩土工程研究所,湖南 长沙 410082)
在桥梁、海洋等桩基的施工与服役过程中,桩基除承受竖向荷载外,往往还可能同时受到风荷载、汽车制动力、波浪冲刷、地震作用等水平荷载的作用。因此轴向、横向荷载作用下单桩的受力变形分析非常重要。目前高层建筑、桥梁及海洋工程的桩基设计中,常规的做法是将轴向荷载与横向荷载分开考虑,分别计算轴向与横向荷载作用下桩身的内力与位移,而后基于小变形假定进行叠加,该种叠加的方法虽计算相对简单,但未考虑轴向荷载与横向荷载作用引起的耦合效应,不能充分反映轴横向荷载作用下单桩的受力变形实际。
已有的室内试验及数值分析结果均表明[1-5]:轴向荷载对水平受荷桩的承载性状有较大影响,如“P-△效应”等,且轴横向荷载存在较为复杂的相互作用。日本学者横山幸满曾指出[6]:应力叠加的原理并不适用桩体同时承受轴向与横向荷载的情况。
为此,轴横向荷载共同作用下单桩的受力变形应考虑轴横向应力的耦合作用,目前相关的理论研究成果主要有:赵明华等[7-8]基于“m法”,求得了考虑轴横向荷载共同作用下的柔性桩解析解,并对基桩的特性进行了深入的研究。李微哲等[9]通过假定地基系数满足(mz+C)的线性增长,探讨分析了轴横向荷载偏心情况下的单桩内力与位移;梁发云等[10]基于小变形假定对轴横向荷载共同作用下的单桩进行了研究,并针对其主要影响因素进行了分析。张磊等[11-12]利用地基反力法求得了轴横向受荷桩的半解析解,研究了自由段桩长及地基反力系数的分布情况等因素对单桩内力与变形的影响;Liang等[13]基于Mindlin方程提出了轴横向受荷桩的有限元解。张玲等[14]基于Winkler弹性地基梁理论,利用相邻单元的连续条件与矩阵传递法研究了地基成层性对轴横向受荷桩的影响。周立朵等[15]基于p-y曲线法研究了轴横向荷载作用下的单桩桩土相互作用,得到了荷载-位移曲线、弯矩分布等规律。Zhu等[16]通过矩阵传递法研究了轴向力及其沿桩身的分布对水平受荷响应的影响。
但上述理论分析方法中,m值的选取与p-y曲线形式的确定不能直接从土工试验中获得,而能量法的优点在于所需的土体参数较易获得,且可在一定程度上考虑桩土复杂的相互作用。因此有学者尝试采用能量法研究荷载作用下单桩的受力变形[17-18]。而对于水平荷载作用下的单桩,Sun等[19]建立了土体在柱坐标下的位移方程,并采用能量法去考虑水平受荷桩的受力与变形,Zhang等[20]、徐洞斌等[21]分别通过能量原理建立了水平荷载作用下桩土体的能量方程,并通过有限差分求得了单桩在水平荷载作用下的受力响应。但上述研究仅针对水平受荷桩而言,未考虑轴向荷载的影响。为此,本文拟在前人的基础上,基于最小势能原理,并结合幂级数法得到轴横向荷载作用下单桩桩身水平位移及内力的解答,以期为工程实际中轴横向荷载下桩基的计算分析提供参考。
1 轴横向荷载作用下单桩的受力变形分析
1.1 计算模型的建立
单桩在轴横向荷载作用时,其桩身因水平荷载产生了较大的水平位移与弯矩,而轴向力作用使得桩身会产生附加弯矩,出现一定的压曲,这个附加弯矩的存在又会使得桩身的水平位移增大,而轴向力引起的桩身水平位移是非线性的,故建立如图1所示模型。
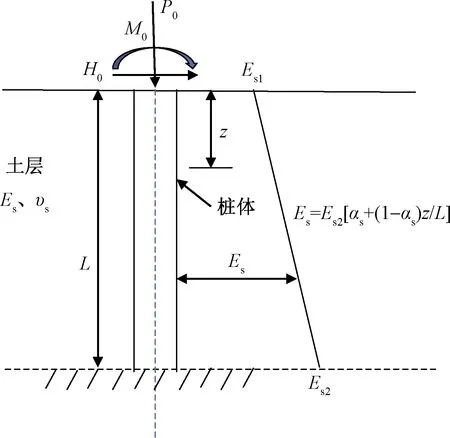
图1 单桩受力计算模型示意图Fig.1 Schematic diagram of the calculation model for pile
如图1所示的桩-土体系中:桩长为L(m);桩身半径为R(m);桩身抗弯刚度为EPIP;桩顶作用水平力H0,轴向荷载P0,弯矩M0。桩周土体弹性模量为Es,泊松比为νs;考虑桩周土体模量沿深度的变化,其变化形式参考文献[20],桩周土体在地面处的弹性模量为Es1,在桩底处弹性模量为Es2,桩身范围内距桩顶z深度处土体的弹性模量为:
Es=Es2[αs+(1-αs)z/L]
(1)
式中:αs——桩周土弹性模量沿深度的变化系数,αs=Es1/Es2。
1.2 桩土体系能量方程的建立
本文采用Sun等[19]提出的土体在柱坐标下的位移模式:

(2)
式中:u,w,v——沿径向、轴向、转角方向的位移,如图2所示;
r,θ,z——柱坐标径向、轴向与转角方向;
u(z)——桩身随深度z变化的位移函数;
φ(r)——r方向土体的无量纲位移函数。

图2 坐标系与位移分量图Fig.2 The coordinate system and displacement components
根据弹性力学几何关系与本构关系可得:

(3)

(4)
式中:εrr,εθθ,εzz——r,θ,z方向的正应变分量;
γrθ,γθz,γzr——rθ,θz,zr方向的剪应变分量;
σrr,σθθ,σzz——r,θ,z方向的正应力分量;
τrθ,τθz,τzr——rθ,θz,zr方向的剪应力分量。
则桩土体系中各部分能量分别可表示为[22]:

(5)

(6)
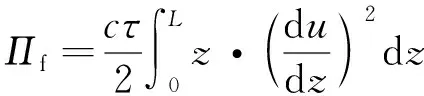
(7)

(8)
ΠH=-H0·u|z=0
(9)

(10)
式中:c——桩截面周长;
τ——桩侧摩阻力,根据文献[23]可采用静载试验获得或根据地区经验值取得;
Πpile,Πsoil,Πf,Πp,ΠH,ΠM——桩身应变能、土体应变能、桩侧土体摩阻力势能、桩顶竖向荷载势能、桩顶水平荷载势能及桩顶弯矩势能。
桩土体系总能量方程为:
Π=Πpile+Πsoil+Πf+ΠP+ΠH+ΠM=
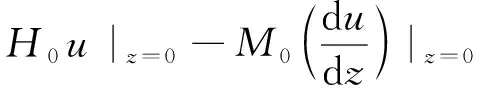
(11)
将式(3)、式(4)代入式(11),可得桩土体系总能量方程为:

(12)
1.3 桩、土位移控制方程
由最小势能原理可知,δП=0,由式(12)求变分可得式(13):
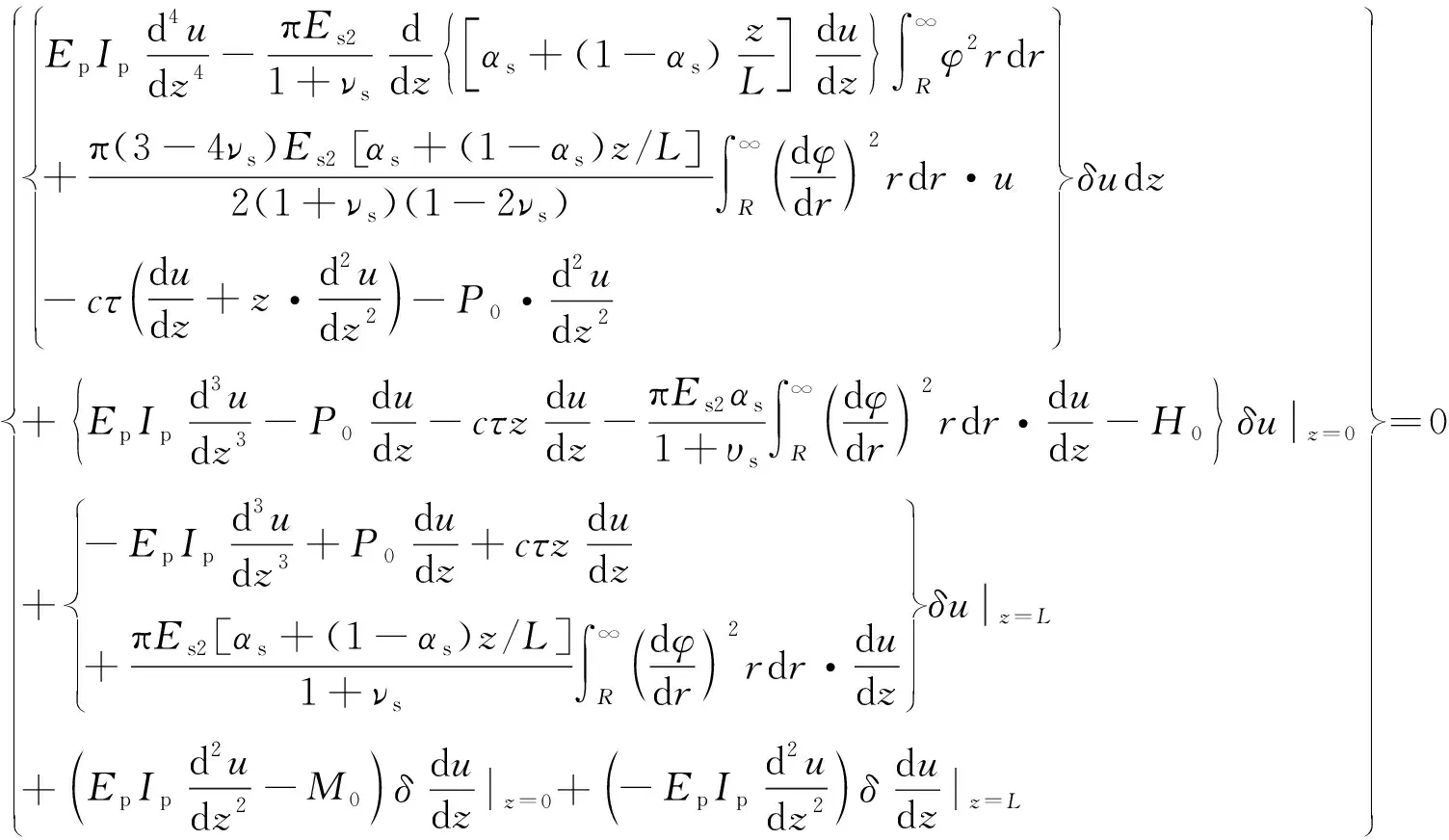
(13)
故由式(13)可推得桩身位移控制方程(14)及沿桩身任意深度处弯矩M及剪力H的表达式(17):
(0≤z≤L)
(14)
其中令:
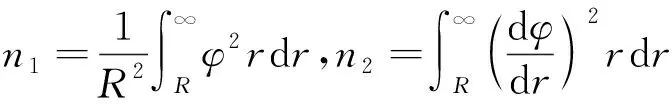
(15)
即桩身位移控制方程可化为:
(0≤z≤L)
(16)
桩身任意深度处弯矩M及剪力H为:

(17)
同理,式(12)对φ取变分可得土体位移控制方程:

(18)
式中:ψ——无量纲系数,决定了水平位移随径向r方向减小的速度。
ψ可以表示为:
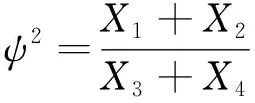
(19)
其中Χ1,Χ2,Χ3,Χ4分别为:
式(18)满足边界条件:当r=R时,φ(r)=1,当r→∞时,φ(r→∞)=0,则有:
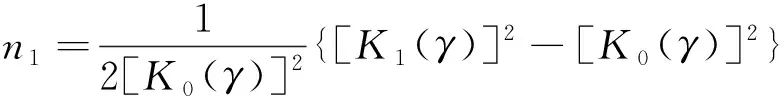
(20)
(γ2+1)[K1(γ)]2}
(21)
式中:K0(·),K1(·)——修正后的第二类贝塞尔函数。
1.4 桩身位移控制方程的解
式(14)可采用幂级数法求解,具体求解过程参考文献[7],故可得其解为:

(22)

式中:a0,a1,a2,a3——待定系数。
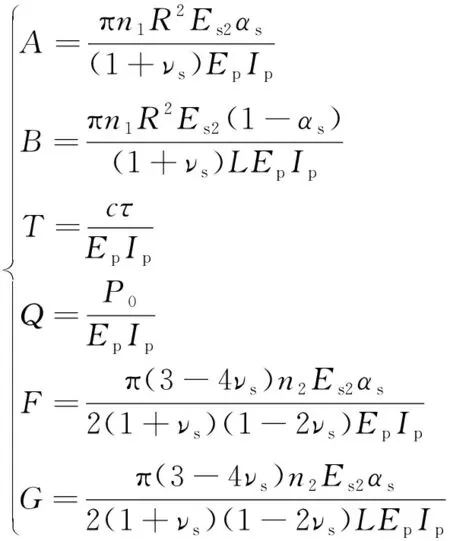
(23)
由式(22)可知桩身位移方程的幂级数函数均可由系数a0,a1,a2,a3表示,而a0,a1,a2,a3可通过联立桩顶与桩底的边界条件进行求解。
其中边界条件可由式(13)推得,表达式为:
(24)

(25)
假定桩顶位移u0、转角φ0、弯矩M0以及剪力H0已知,结合式(22)、(24)、(25)可得:
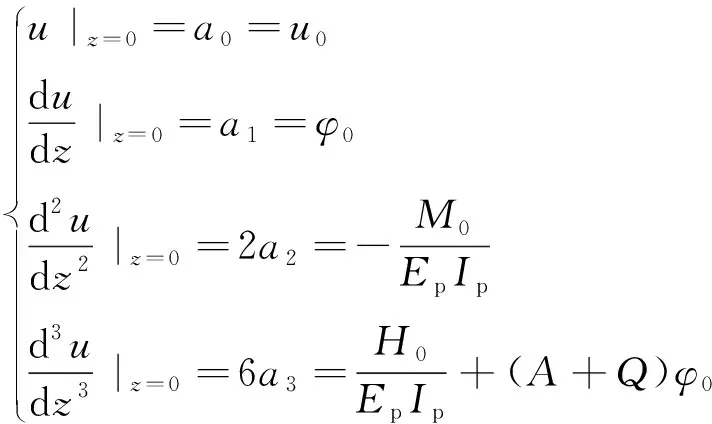
(26)
由上述边界条件可求得a0,a1,a2,a3的值。再选定合适的项数,即可求得水平位移的函数表达式,其具体流程如图3所示。当桩底嵌入岩层或者桩底土层较坚硬的时候,认为桩端为固定边界。为方便求解,下文将采用桩顶自由、桩底固定的边界条件进行求解验证。
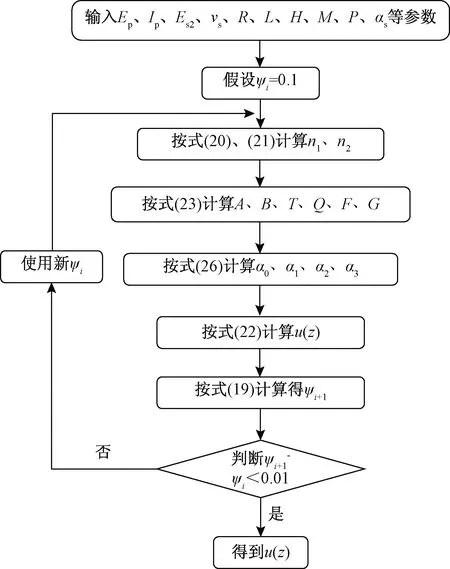
图3 桩身水平位移求解程序图Fig.3 Program diagram for solving horizontal displacement of pile
2 算例分析
2.1 算例1
Kerisel等[24]对水平受荷单桩进行了室内模型试验。模型桩桩长L=4.65 m,桩径D=0.36 m,桩顶自由,桩底嵌固。受到的水平荷载H0=60 kN,弯矩M0=69 kN·m,桩身的弹性模量Ep=20 GPa,土体的弹性模量Es=9.233 MPa。土体的泊松比νs=0.3,桩周土模量沿深度的变化系数αs=1。Filho等[25]通过有限元与边界元软件验证了其试验结果,图4给出了本文方法计算结果与Kerisel等模型试验结果、Filho等有限元结果、《公路桥涵地基与基础设计规范》(以下简称规范法)推荐的简化方法计算结果的对比分析。
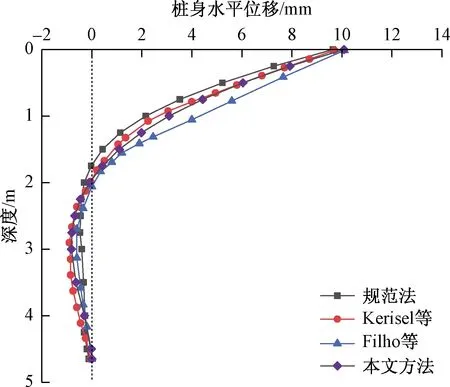
图4 水平荷载作用下的桩身水平位移Fig.4 Lateral displacement of pile due to the horizontal load
由图4可知,本文方法计算所得桩身水平位移结果与上述几种方法所得结果都比较接近,而且相比较于Filho等有限元方法,本文计算方法所得的桩身水位位移更接近于Kerisel模型试验结果。就桩顶(z=0 m)水平位移而言,Kerisel模型试验结果为9.7 mm;Filho等有限元方法结果为10.1 mm,相对比试验结果误差为4.12%;本文方法计算所得桩顶位移为10.08 mm,相对比试验结果误差为3.9%。由此可见本文方法可用于分析水平受荷桩的受力变形分析。
2.2 算例2
肖世伟等[26]利用有限元方法对马桥河桥钻孔桩基足尺试验所得结果进行了模拟分析,并将实测数据进行反算,给出了地基系数m=1.398×104kN/m4与桩身弹性模量Eh=3.188×107kN/m2,试验的桩体参数分别为:桩长L=17.0 m,桩径D=0.85 m,土层泊松比νs=0.3,桩周土模量沿深度的变化系数αs=1,则公式(1)即简化为Es=Es2,土体弹性模量Es2=6 MPa,本文方法计算所得桩顶位移与文献[26]结果如表1所示。此外,为比较本文计算桩身位移沿桩身的分布情况,以文中参数建立弹性有限元模型,取桩顶轴向荷载为313.60 kN的情况,本文方法计算的桩身位移与有限元模拟的桩身位移对比结果如图5所示。
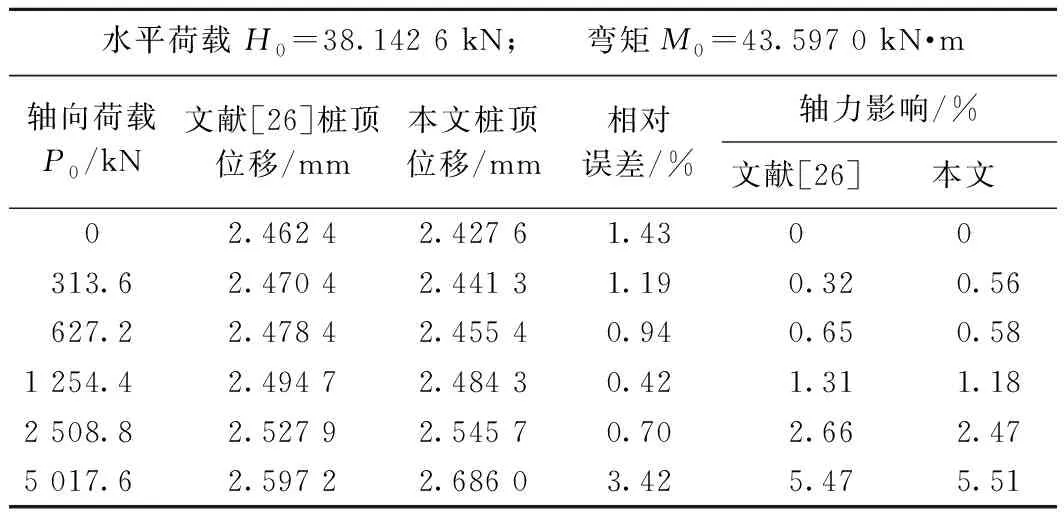
表1 本文方法与文献[26]结果对比
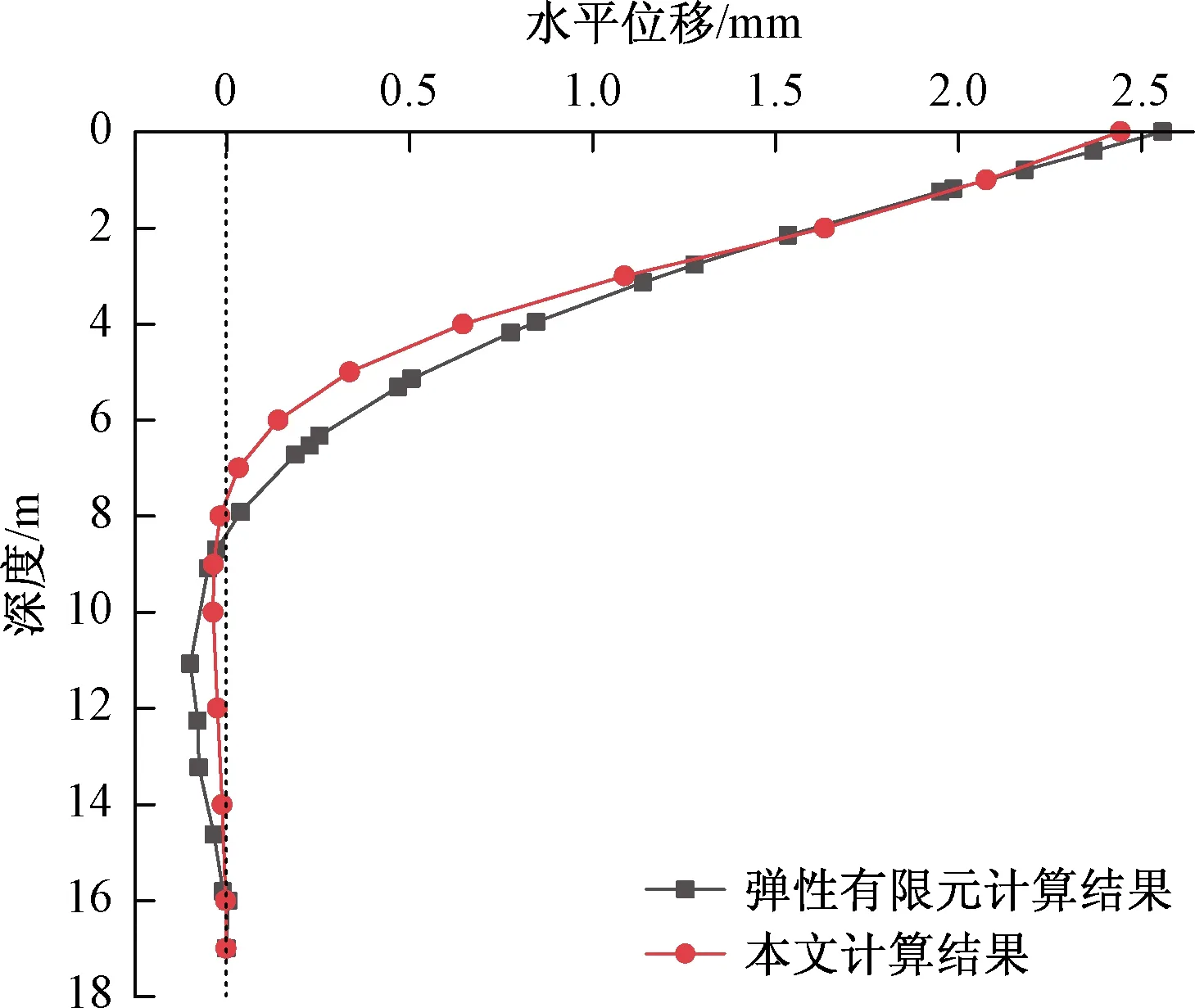
图5 桩身水平位移图Fig.5 Lateral displacement of pile
由表1可知,本文方法计算所得结果与文献[26]所得结果基本吻合,且随着轴向荷载的增大,对桩顶水平位移的影响也随之增大,且由图5可知,本文方法计算所得的桩身位移与弹性有限元分析所得结果拟合较好,可应用于工程实际。
2.3 算例3
Cho等[27]对水平受荷的嵌岩桩基进行了多组现场横向荷载试验,该工程位于美国北卡罗来纳州的一个桥梁替换项目,其中一组其桩侧有2层地基土,第一层为深度L0=1 m的砂土层,第二层为深度L1=3.3 m的泥板岩;桩长为L=4.3 m,桩体半径R=0.38 m,桩体弹性模量Ep=24.8 GPa。
Yang等[28]采用地基反力法与变分原理对该工程进行了验证分析,并根据Cho等试验所得结果的p-y曲线进行反算,假设桩侧路基反力模量Kh0在地面处为0,沿深度线性增加,求得首层土其增加系数为nhs,0=19.5 MN/m3。泥板岩内的路基反力模量Kh1=180.6 MPa,nhs,1=393.3 MN/m3,路基反力模量的经验公式如式(27)所示,其计算模型如图6所示。
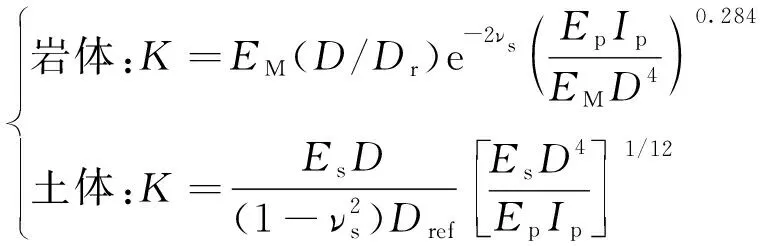
(27)
Dr=0.305 m,Dref=1.0 m
式中:K——路基反力模量;
EM——岩体模量。
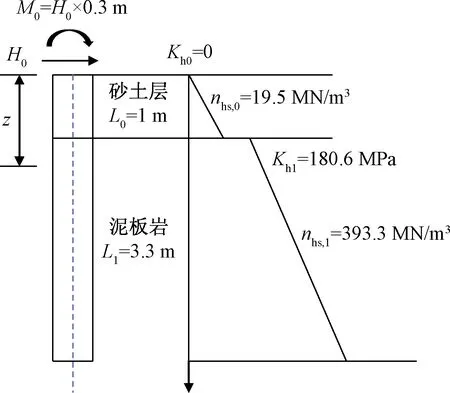
图6 Yang等计算模型图Fig.6 Schematic diagram of the Yang calculation model
利用本文能量法对该算例进行验证分析,桩体与土体参数如上所述,本文所用的土体弹性模量与路基反力模量的换算公式为[29]:

(28)
式中:Kh——路基反力模量。
桩体在泥板岩内基本不发生水平位移,因此为简便计算,本文利用砂土层的参数进行验证,由式(28)可得砂土层底土体弹性模量Es2=17.73 MPa,取桩周土模量沿深度的变化系数αs=0.1,土体泊松比取为νs=0.3,计算结果如图7所示,其中Yang所用p-y曲线法为利用Cho试验结果反算求得。
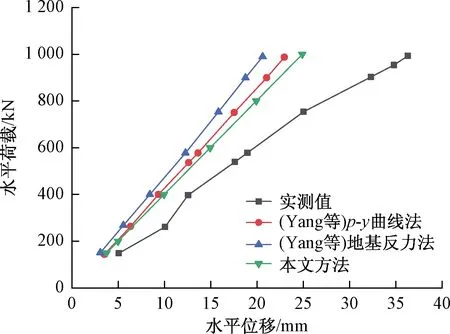
图7 水平荷载作用下的桩身水平位移Fig.7 Lateral displacement of pile due to the horizontal load
由图7可知,本文方法所得的桩顶位移较文献[28]更接近实测值。
3 参数分析
3.1 桩土弹性模量比的影响分析
取桩顶自由,桩底嵌固,桩的长径比为L/D=15,取桩周土模量沿深度的变化系数αs=1,土的泊松比取为νs=0.3,桩土的弹性模量比值Ep/Es2分别为100,500,1 000,2 000与5 000。桩顶水平荷载与轴向荷载分为取为H0=120 kN,P0=60 kN。其计算结果如图8所示。

图8 桩土弹性模量比变化下的桩身水平位移和桩身弯矩Fig.8 Horizontal displacement and bending moment of pile under the variation of elastic modulus ratio of pile to soil
由图8可知,桩身水平位移随着桩土模量比的增大而逐渐增大,桩顶处水平位移在桩土模量比Ep/Es2=5 000处急剧增大,在轴向压力的作用下,桩身最大弯矩点不断向下移动。而当轴向荷载由0变为60 kN时,其桩顶水平位移减小,桩身最大弯矩点下移,轴向荷载的存在使得桩身出现一定的压曲现象,桩身的水平位移与弯矩均出现了增大的情况。
3.2 桩体长径比的影响分析
取桩顶自由,桩底嵌固,桩土弹性模量比Ep/Es2=1 000,取桩周土模量沿深度的变化系数αs=1,土体的泊松比为νs=0.3,桩体长径比L/D分别为5,10,15,20,25。桩顶水平荷载与轴向荷载分为取为H0=120 kN,P0=60 kN。为比较方便,将桩长进行归一化可得图9。
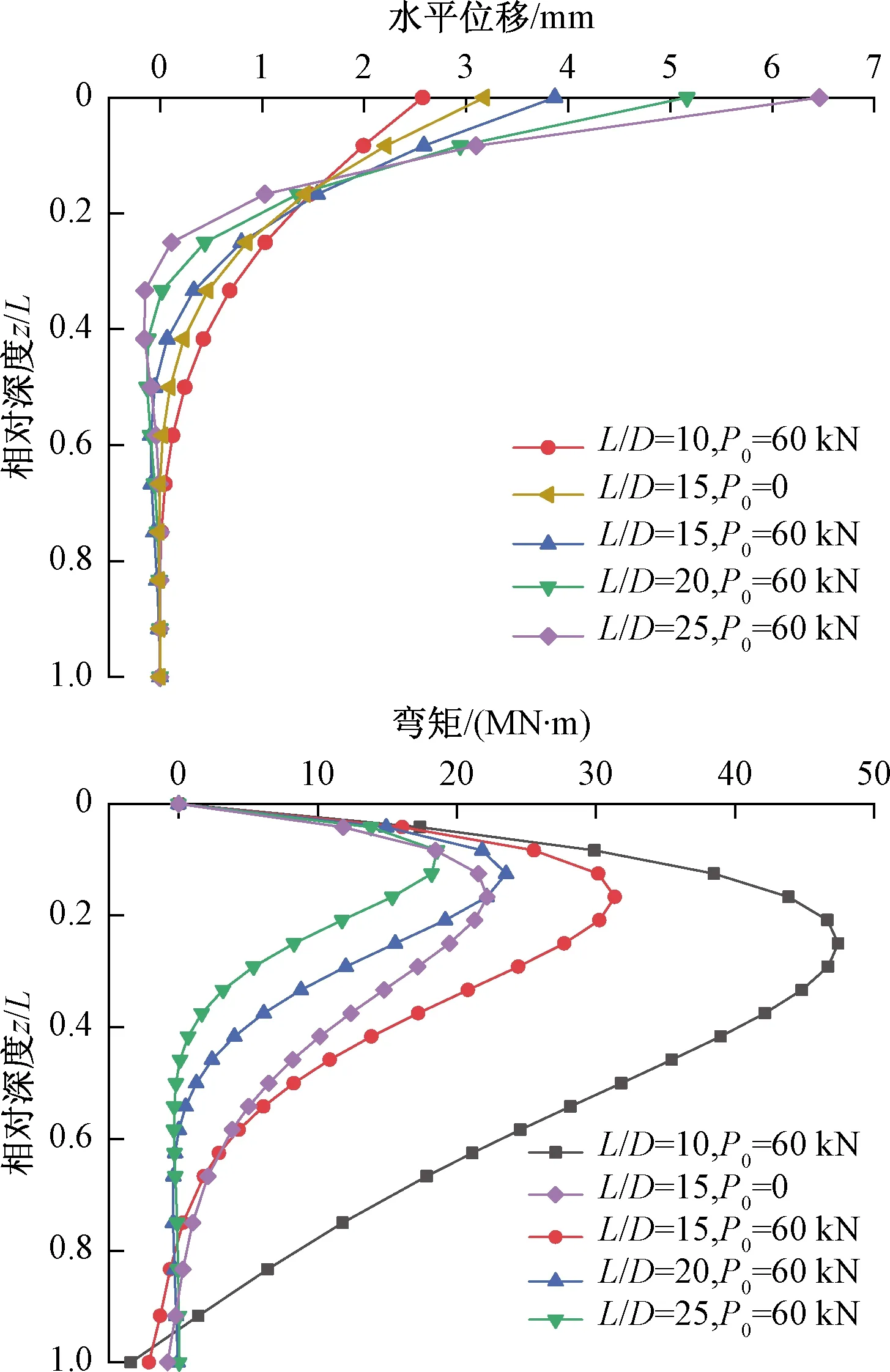
图9 长径比变化下的桩身水平位移和桩身弯矩Fig.9 Horizontal displacement and bending moment of pile under the variation of length-diameter ratio
由图9可见,当桩顶轴向荷载为60 kN时,桩的工作性状会随桩长径比的变化而发生改变。当桩的长径比L/D大于10时,桩身出现反弯。其原因是随桩的长径比增大,桩体表现出柔性桩性质,近地面处的土体发生屈服,导致桩顶水平位移增大;而当长径比L/D小于10时,桩体受力近似于刚性桩,桩身位移曲线近似为直线,且桩身不出现反弯点。此外,桩的长径比对桩身弯矩也有较大影响。随着桩的长径比L/D的增大,桩身中上部的弯矩变化明显,桩身最大弯矩减小,且最大弯矩点逐渐上移。当长径比变化时,轴向荷载对桩身位移与弯矩的影响与桩土模量比变化时的影响类似。
3.3 轴向荷载的影响分析
取桩顶自由,桩底嵌固,桩的长径比L/D=15,取桩周土模量沿深度的变化系数αs=1,土的泊松比取为νs=0.3,桩土弹性模量比值Ep/Es2=1 000。桩顶水平荷载取H0=120 kN,轴向荷载P0分别为0,600,1 200,2 400,4 800 kN。计算结果如图10所示。
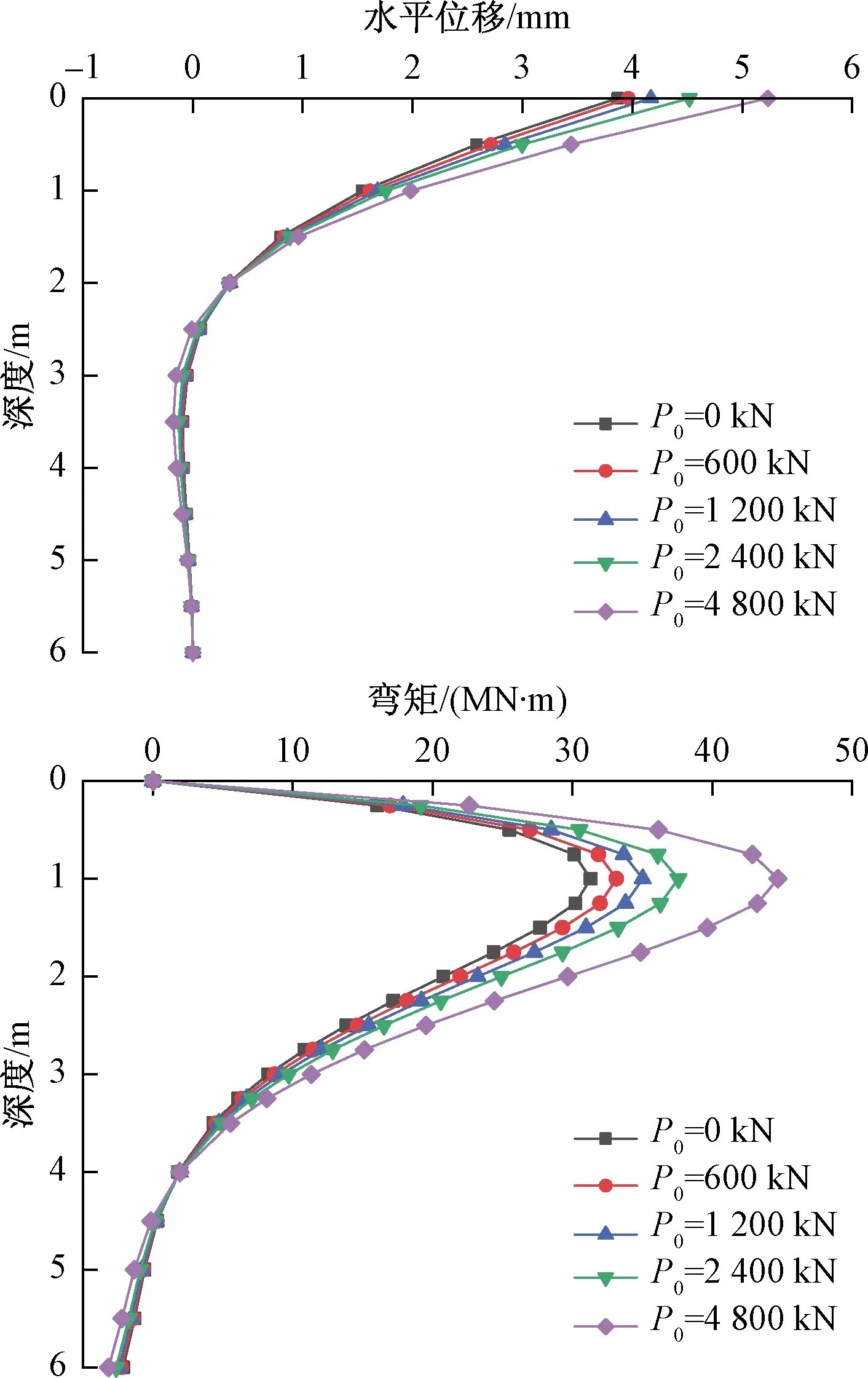
图10 轴向荷载变化下的桩身水平位移和桩身弯矩Fig.10 Horizontal displacement and bending moment of pile under the variation of axial load
由图10可知,轴向荷载对桩身水平位移的影响主要位于桩身上部2 m,约为10倍桩径范围内。随着轴向荷载的增加,桩身最大弯矩点不断下移,其影响范围约位于地面以下4 m,约为20倍桩径范围内。与文献[10]所得结论基本一致。而且,随着P0/H0比值的增大,轴向荷载对桩身水平位移及弯矩的影响明显增大,其主要原因在于由轴向荷载引起的桩身挠曲变形是非线性的。
3.4 αs的影响分析
桩周土体的弹性模量对桩身内力及变形有较大影响,由式(1)可知,系数αs决定了桩周土体弹性模量沿深度的变化趋势,故对该系数做参数分析。
取桩顶自由,桩底嵌固,桩的长径比为L/D=15,土的泊松比取为νs=0.3,桩土的弹性模量比值Ep/Es2=1 000,αs分别取为1,0.8,0.6,0.4,0.2。桩顶水平荷载与轴向荷载分为取为H0=120 kN,P0=60 kN,计算结果如图11所示。
由图11可知,当桩顶轴向荷载由0增加到60 kN时,桩顶水平位移从3.17 mm增大为3.86 mm,增大比例为21.7%,桩身最大弯矩由22.2 kN·m增大到31.36 kN·m,增大比例为41.3%。而当桩顶轴向荷载不变时,随桩周土模量沿深度的变化系数αs从1减小到0.2时,桩顶水平位移的增大比例分别为19.17%、47.67%、94.3%、190.2%,桩顶弯矩的增大比例分别为10.9%、25.7%、50.7%、95.7%。可知当桩周土模量沿深度的变化系数过小时,即上部土层弹性模量过小,会导致桩顶位移急剧增大,桩身弯矩急剧增大,最大弯矩点逐渐下移,故在实际工程中可采取对浅部土层进行换填等方法去改善土质,从而控制桩顶的水平位移与桩身弯矩。

图11 αs变化下的桩身水平位移和桩身弯矩Fig.11 Horizontal displacement and bending moment of pile under the variation of αs
4 结论
(1)本文基于最小势能原理建立了轴横向荷载作用下单桩的能量方程,一定程度上考虑了轴横向荷载的耦合作用,将桩顶的轴横向荷载、桩侧摩阻力及桩土相互作用视为一个整体进行分析,并给出了幂级数解答。
(2)参数分析结果表明:①桩土弹性模量比对单桩内力与变形有较大影响。②桩身长径比小于10时,桩体受力近似刚性桩容易引起桩身失稳。③轴向荷载对桩身水平位移与弯矩的影响主要集中与桩身上部20倍桩径范围内,而对深处影响较小。④桩周土模量沿深度的变化系数αs小于0.6时,单桩桩身水平位移与弯矩受其影响很大。
(3)本文方法可进一步推广到多层地基以及桩身变截面等情况。此外,为求解方便,本文仅以土体弹性模量沿深度线性变化的角度考虑土体的非线性,未考虑土体的弹塑性变形,这将在后续的工作中进一步深入研究。
