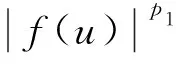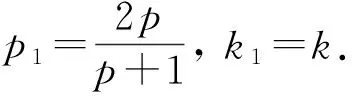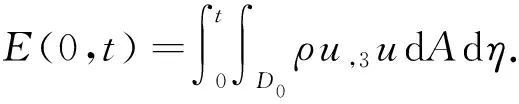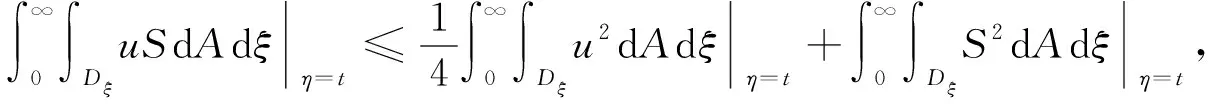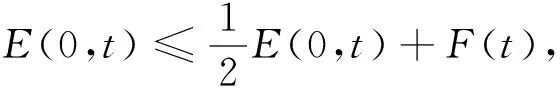一类二阶拟线性瞬态方程组的Phragmén-Lindelöf型二择性结果
2020-09-27李远飞肖胜中郭连红
李远飞, 肖胜中, 郭连红, 曾 鹏
(1. 广东财经大学华商学院 数据科学学院, 广州 511300; 2. 广东农工商职业技术学院, 广州 510507)
1 引言与预备知识
Saint-Venant原理[1]在应用数学领域应用广泛, 其早期研究主要集中于椭圆方程的初边值问题, 此后各种类型的抛物方程得到广泛关注[2-7]. 通常情况下, 研究抛物方程的空间性质时需假设在柱体的无限端解趋于零或趋近于一个瞬态层流, 并通常假设在柱体的侧面上满足零边界条件. 经典的二择一定理不必假设方程组的解在无限端趋于零, 而是证明调和函数随与有限端距离的增大或者呈指数(多项式)增长, 或者呈指数(多项式)衰减. Horgan等[8]考虑了定义在一个柱体区域Ω⊂3上的Laplace方程, 假设解在Ω的边界上满足非线性条件, 证明了Laplace方程的解或者指数式(或多项式)增加, 或者指数式(或多项式)衰减; 如果在柱体的侧面上施加不同的非线性条件, 利用文献[9]的方法, 文献[10]得到了解的二择一定理; 文献[11]研究了二维双调和方程的Phragmén-Lindelöf二择一定理, 并着重考虑了3种不同的半无穷柱体区域; 文献[12]给出了二维瞬态的Stokes 流体方程的二择一结果; 文献[13]考虑了定义在一个三维柱体上的稳态拟线性方程
(ρ(x,u,u)u,i),i=f(u),
当方程的解在柱体的侧面上满足零边界条件或其次Neumann边界条件时, 通过对非线性项做出一定的限制, 得到了解的二择一定理.
本文令Ω表示三维区域上的半无限柱体,Dz表示Ω在x3=z处的横截面,D表示Ω在坐标平面x1Ox2上的横截面, 即Ω={(x1,x2,x3)|(x1,x2)∈Dx3,x3>0}. 令∂Dx3表示Dx3的边界,z是x3轴上的一个动点,Ωz记为
Ωz={(x1,x2,x3)|(x1,x2)∈Dx3,x3≥z≥0},
其中Dx3是与x3相关的一个光滑区域, 例如
uf(u)≥ku2p/(p-1),p>1,k>0;
(5)
g(x1,x2,t)是大于零的给定函数且满足兼容性条件g(x1,x2,t)=0, (x1,x2,t)∈D0×(0,T)和g(x1,x2,0)=0; 在式(1)中假设ρ满足
(6)
其中m1,M1和M2都是大于零的常数.
目前, 关于半无穷柱体上解的二择一性质的研究文献报道较少, 本文将文献[13]中的二择性定理推广到瞬态方程中, 受文献[11]的启发, 考虑3种不同的半无穷柱形区域, 分别给出解的二择性. 用u的L2积分控制u的L2积分, 即

引理1若w|∂Dz=0, 则存在一个依赖于区域Dz大于零的函数r(z), 使得

(7)
其中r(z)=|Dz|表示区域Dz的面积.
证明: 设P是Dz内的一个点. 令P1和P2分别表示过点P平行于x1坐标轴的直线与∂Dz的交点, 令Q1和Q2分别表示过点P平行于x2坐标轴的直线与∂Dz的交点. 首先, 注意到
所以

(8)
类似地, 有
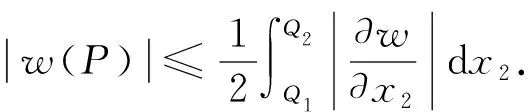
(9)
结合式(8),(9), 有
再利用不等式(a+b)2≤2(a2+b2)(a,b>0)及Hölder不等式, 可得式(7). 证毕.
2 能量表达式
下面先定义一个能量表达式, 再利用微分不等式技术推导出一个关于该能量表达式的一阶微分不等式, 从而得到解的二择一结果. 为此, 利用方程(1), 可得恒等式
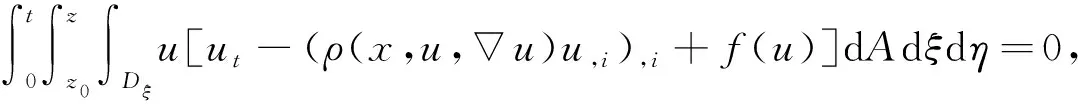
(10)
其中z0≥0是x3坐标轴上的点. 在式(10)中利用分部积分, 可得
令

(12)
于是由式(11)可得
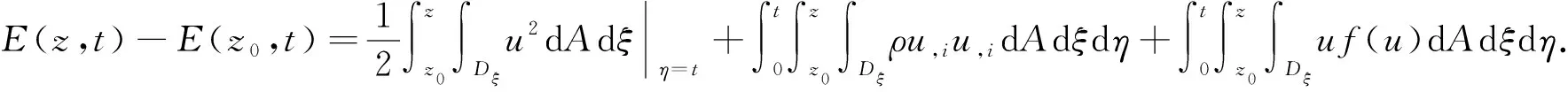
(13)
对式(13)求导, 可得
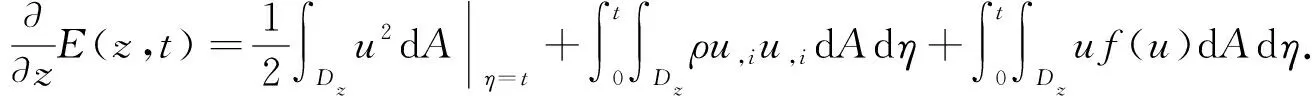
(14)
根据Hölder不等式和算术几何平均不等式, 由式(12)可得

(15)
利用式(6)和引理1, 可得
把式(16)代入式(15)再结合式(14), 可得
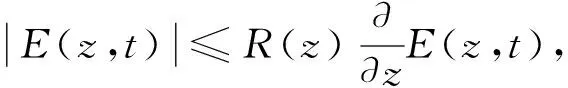
(17)


(18)

(19)
3 二择性定理
首先考虑一个一般区域, 即柱体Ω的母线平行于x3坐标轴. 此时, 柱体Ω在任意z∈[0,∞)处的横截面都相等, 所以Dz的面积不依赖于z, 记r(z)=r0>0. 这种区域是大多数研究者关注的情形[12-13], 但本文考虑的问题更复杂.
3.1 半无穷柱体
对式(11)定义的E(z), 利用式(18)和式(19)分为如下两种情形分析.
1) 存在一个点z0>0, 使得E(z0)>0.
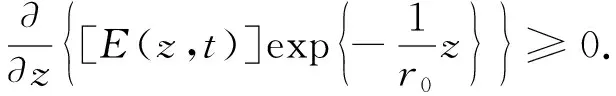
(20)

2) 对所有的z≥0, 都有E(z)≤0.
此时, 式(19)成立, 所以

(22)
对式(22)从0到z积分, 可得

(23)
式(23)表明当z→∞时, -E(z)指数式衰减于零. 对式(14)从z到∞积分, 可得
(24)
其中

(25)
综上, 可得以下Phragmén-Lindelöf型二择一定理:
定理1设u为问题(1)-(4)在一个半无穷柱体Ω上的解, 其中函数ρ满足式(6), 非线性项f(u)满足式(5). 则对式(12)定义的E(z,t), 当z→∞时或者指数式增长, 或者指数式衰减, 即或者式(21)成立, 或者式(24)成立.
3.2 扩展区域
下面讨论当柱体Ω的横截面随z→∞不断扩大的情形, 此时的柱体形状像一个喇叭花. 显然柱体截面增大的速度过快, 得不到二择性结果. 因此必须对柱体做一定的限制. 下面对这种柱体给出一个例子, 即

(26)
根据R(z)的定义可知, 在该区域上R(z)满足
1
(27)
下面分两种情形讨论.
1) 存在一个点z0>0, 使得E(z0)>0.
此时, 与3.1中的情形1)类似, 有E(z)≥E(z0)>0,z≥z0>0. 因此由式(18)可得
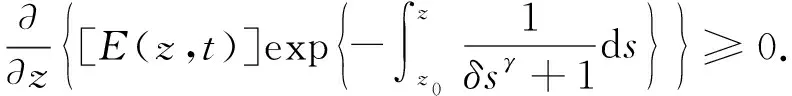
(28)
对式(28)从z0到z积分, 可得
再由式(13)可得
由于0<γ≤1, 所以

(30)
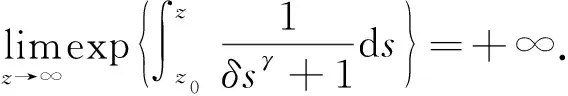
2) 对所有的z≥0, 都有E(z)≤0.
此时, 由式(19)可得
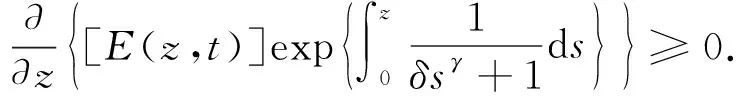
(31)
对式(31)从0到z积分, 可得

(32)
综上, 可得以下Phragmén-Lindelöf型二择一定理:
定理2设u为问题(1)-(4)在一个半无穷柱体Ω上的解, 其中函数ρ满足式(6), 非线性项f(u)满足式(5). 如果柱体Ω的横截面Dz满足式(27), 则对式(12)定义的E(z,t), 当z→∞时, 或者无限增长, 或者无限衰减, 即或者式(29)成立, 或者式(33)成立.
注1在定理2中, 如果γ=1, 则
表明当z→∞时,E(z,t)或者呈多项式增长, 或者呈多项式衰减, 衰减速度至少与z1/δ相同. 如果0<γ<1, 则可做如下处理:
从而
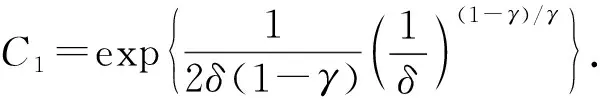
注2如果R(z)=δzγ+1,δ>0,γ>1, 则式(30)中的极限收敛, 从而得不到定理2的结果. 表明柱体截面增大的速度过快, 因此得不到衰减性结果.
3.3 特殊区域
假设R(z)满足
1 (34) 下面仍分两种情形进行分析. 1) 存在一个点z1>0, 使得E(z1)>0. 此时, 与3.1中的情形1)类似, 有E(z)≥E(z0)>0,z≥z1>0. 取z0=max{e,z1}, 类似3.2中情形1)的计算, 可得 下面证明式(35)左边的积分是无限增加的. 因为 (36) 2) 对所有的z≥0都有E(z)≤0. 此时, 由式(19)可得 (37) 对式(37)从e到z积分, 可得 (38) (39) 综上, 可得以下Phragmén-Lindelöf型二择一定理: 定理3设u为问题(1)-(4)在一个半无穷柱体Ω上的解, 其中函数ρ满足式(6), 非线性项f(u)满足式(5). 如果柱体Ω的横截面Dz满足式(34), 则对式(12)定义的E(z,t), 当z→∞时或者无限增长或者衰减, 即或者式(36)成立, 或者式(39)成立. 由定理1~定理3可知, 在衰减的情形下, 要使衰减估计有意义, 必须推导-E(0,t)的上界. 假设 (40) (41) 同时由式(25), 可得 (42) 下面引入一个辅助函数: S(x1,x2,x3,t)=g(x1,x2,t)e-σx3, 其中σ是一个大于零的常数. 利用分部积分和方程(1), 有 根据Hölder不等式和算术几何平均不等式, 可得 (44) (45) 再利用式(40), 可得 其中ε1是一个大于零的任意常数. 类似地, 由式(5), 有 其中ε2是一个大于零的任意常数. 取适当的ε1和ε2, 使得 (48) 其中 所以由式(48)可得E(0,t)≤2F(t). 取适当的σ, 即可得E(0,t)的上界.

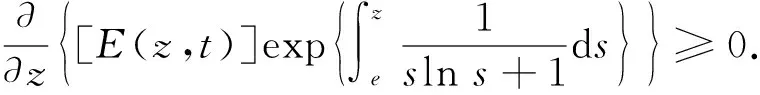

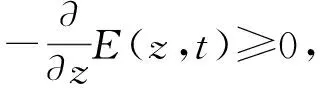

4 全能量估计