基于最优簇头数的环形无线传感器网络分簇算法
2020-09-27王宏志武莎莎鲁晓帆胡黄水王出航郭嫚嫚
王宏志, 武莎莎, 鲁晓帆, 胡黄水, 王出航, 郭嫚嫚
(1. 长春工业大学 计算机科学与工程学院, 长春 130012;2. 吉林建筑科技学院 计算机科学与工程学院, 长春 130114;3. 长春师范大学 计算机科学与技术学院, 长春 130032)
无线传感器网络(WSNs)是由许多传感器节点以多跳或自组织形式组合成的分布式传感器网络[1-2], 在环境观察、 军事应用、 建筑监控、 医疗保健、 家居和汽车等领域应用广泛[3]. 无线传感器网络中由于节点的工作任务不同, 因而存在传感器网络中节点能量消耗不均匀等问题. 无线传感器网络的拓扑结构在降低网络节点能量消耗、 平衡网络能量方面具有重要作用[4-5], 其中分簇算法的设计直接影响网络能效. 低能量自适应聚类层次结构(low-energy adaptive clustering hierarchy, LEACH)[6]是WSNs的第一个聚类协议, 其主要思想是通过节点轮流充当簇头(cluster head, CH)节点均衡网络能耗, 但CH节点的选择未考虑节点的剩余能量, 将导致网络的负载不均衡. HEED[7](hybrid, energy-efficient, distributed clustering approach for Ad Hoc sensor networks)算法是LEACH算法的一种改进算法, 其虽然把节点的剩余能量作为选择CH节点的因素, 但路由阶段所需开销较大.
目前, 基于多跳通信及分簇的方法已有很多: 刘志等[8]采用分环的方式实现CH节点间的多跳通信, 但在选取CH节点时, 未考虑内环CH节点的剩余能量, 导致某些内环CH节点的负荷过重; 文献[9]采用一种能量高效的分簇算法, 每轮结束后都重新选举CH节点, 减少了能量的浪费, 但复杂的参数限制了网络性能; 文献[10]采用环形多级分簇结构, 使节点与基站(base station, BS)间拥有最小的通信能耗; 文献[11]提出了在不等级环模型的最内环引入非均匀分簇的思想, 减少了网络中最内环节点的能量消耗; Sha等[12]提出了基于候选簇头(CCH)实现数据转发, 不仅减少了CH节点的负荷, 也减少了数据上传期间数据溢出的可能性, 但增加了网络能耗; 文献[13]的EUSC(energy efficient unequal sector clustering)算法考虑了网络中中继节点的选择及节点的队列长度; 文献[14]通过替代技术为能量受损的CH节点提供局部补救, 但在循环选择替换节点时, 选为替代节点的剩余能量阈值是固定的; 文献[15]通过使用层间最小能量消耗路由算法建立从CH节点到BS的路由, 提高了网络能效; 文献[16]以节点剩余能量和数据传输能耗为代价选举CH节点, 延长了网络生命周期, 但由于距离BS较近的簇较大, 加重了BS附近CH节点的负荷.

图1 网络模型Fig.1 Network model
为了解决上述问题, 提高网络能效和扩展性, 本文提出一种基于最优簇头数的环形无线传感器网络分簇算法(CAROCN), 该算法主要将网络区域视为若干个圆环组成, 以每个环中能量消耗最小为原则计算出每个环中的最优簇头数, 然后将每个环按相应的最优簇头数分成若干大小不同的网格, 每个网格形成一个簇. 环形网络中最外环的CH节点不需转发上一环的数据, 所以本文又单独考虑了最外环的最优簇头数, 且在CH节点选择时, 考虑了每个环的最优簇头数与相应环中节点数目的比值、 节点的剩余能量及簇成员(cluster member, CM)节点到簇头(CH)节点的最短距离与CH节点到BS距离的关系.
1 CAROCN算法
1.1 网络模型
假设在半径为R的圆形感测区域中均匀分布N个传感器节点, BS位于感测区域的中心. 网络模型如图1所示, 网络环境设置如下:
1) 网络在初始化后节点的位置不再发生变化, BS位于圆形网络的圆心处, 且BS将自己的位置信息发送给所有传感器节点;
2) 每个传感器节点的初始能量相同并具有唯一的ID;
3) 所有来自CM节点的数据由CH节点融合, 且只允许CH节点与BS通信;
4) 网络中链路没有冲突和重传, 并具有很好的连接性.
1.2 最优簇头数
采用文献[4]中的能量消耗模型, 计算距离为d的两个节点之间发送或接收ubit数据所消耗的能量. 能量消耗模型为

(1)
ER(u)=u×Eelec,
(2)

(3)
其中:Eelec为一个传感器节点发送或接收1 bit数据时电子电路所消耗的能量;εfs为采用自由空间模型时的放大参数;εmp为采用多路衰减模型时的放大参数;d0为距离阈值, 本文采用自由空间模型. 融合Ni个传感器节点发送的数据所消耗的能量为EDA, 表达式为
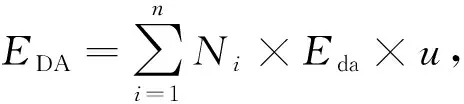
(4)
其中:Eda为融合1 bit数据所消耗的能量;u为数据包的长度.
1.2.1 第n环的最优簇数 最外环的CH节点仅需接收CM节点发送的数据, 然后将这些数据融合成固定长度的数据转发给下一环中的某个CH节点. 假设最外环中每个簇的节点数目为Nn(n≥2,n为正整数),ρ为节点面密度, 最外环最优簇头数为mn, 每个簇所对应的扇形圆心角为θn, 则

(5)

(6)

(7)
同一环中每个簇传输数据所消耗的能量相等, 用En表示. 一个簇的能量消耗包括CH节点的能量消耗Ech和CM节点发送数据给CH节点所消耗的能量Ecm.Ech的表达式为

(8)
其中:l为数据包的长度;dch为CH节点与下一跳之间的欧氏距离, 如图2所示, 其数学表达式为
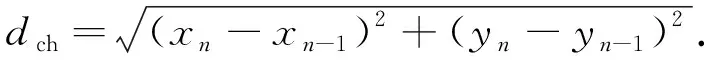
(9)
图2中,A和C是最外环某簇的CH节点,B是A的下一跳CH节点,A和B的坐标分别为A=(xn,yn),B=(xn-1,yn-1). 本文采用自由空间模型, 所以dch (10) (11) 其中dcc表示同一个簇中CM节点到CH节点的距离, 其平方的期望为 (12) 其中dc为一个簇中CM节点到CH节点的最大距离,dc在模型中的表示如图3所示. 图2 簇头节点与簇头节点之间的距离Fig.2 Distance between CH node and CH node 图3 非簇头节点与簇头节点之间的距离Fig.3 Distance between CM node and CH node 其中 (14) 因此, 最外环总能量消耗Etotal为 把式(9)和式(13)代入式(15), 并对mn求导, 可得最外环的最优簇头数为 (16) 其中: (17) 1.2.2 第i环的最优簇头数 除最外环簇的CH节点外, 其他环中的CH节点不仅要接收该簇中CM节点发送的数据, 同时也要接收上一环中某CH节点转发的数据, 将这些数据进行融合, 然后转发到下一跳接收节点. 设第i(i=1,2,…,n-1)环中每个环扇的节点数为Ni, 第i环的最优簇头数为mi, 则第i环中每个簇所对应的扇形圆心角θi为 (18) (19) (21) (22) (23) 其中:dcc*为第i环中CM节点到CH节点的距离;dc*为第i环中CM节点到CH节点的最大距离, 由图3及式(13)可知 (24) 其中 (25) 所以第i环中总能量消耗ETOTAL为 对式(26)求导, 可得第i环的最优簇头数mi为 (27) 其中: (28) 由上述理论可得网络中每个环的最优簇头数mi(i=1,2,…,n), 再根据ω选择每个环中的CH节点,ω=mannual/Nannual表示每环中的最优簇头数mannual占相应环中节点数目Nannual的比值,ω越大表示当前环中CH节点数越多. 为减少CH节点选择的随机性, 提高网络的生命周期, 在选择CH时本文考虑了当前轮次中节点的剩余能量与节点初始能量的关系, 用参数α=Ecj/E0表示, 其中:Ecj表示节点j的当前剩余能量;E0表示节点j的初始能量. 网络在成簇后, CM节点需向CH节点发送数据, CH节点最终将数据发送到BS. 该过程中距离CH节点远的CM节点及距离BS远的CH节点的通信能耗均较大, 所以在CH节点的选择上, 本文考虑了CM节点到CH节点的最短距离和CH到BS距离的关系, 用参数β表示,β=min_djc/dcb, 其中: min_djc表示节点j到CH节点c的最短距离;dcb表示CH节点c到BS的距离. 则CH节点的选举阈值V(Nu)为 (29) 其中:r为当前网络的轮数;S为当前轮开始前网络中非簇头节点集. 为了评估CAROCN算法的性能, 利用MATLAB 2014a软件在网络区域为100 m×100 m和200 m×200 m的仿真环境中进行多次实验, 以网络第一个节点死亡轮数、 网络总能耗、 网络平均节点剩余能量及存活节点数量4个指标分析CAROCN算法的性能, 并与LEACH算法[8]和ACONC算法[16]进行比较. 实验仿真参数设置为: 网络区域100 m×100 m, 200 m×200 m; 节点数量N=100; 节点初始能量E0=0.05 J; 网络环数n=7; 数据报文大小为4 000字节; 自由空间模型参数εfs=1×10-11J/(bit·m2); 发送和接收电路的能耗参数Eelec=5×10-11J/bit. 在网络区域为100 m×100 m和200 m×200 m的监测区域下, 第一个节点死亡的轮数如图4所示. 由图4可见: 在100 m×100 m的网络区域中, 当CH节点轮换次数为345轮时, LEACH算法出现节点死亡, ACONCN算法在498轮时出现节点死亡, 而CAROCN算法的第一个节点死亡轮数比上述两种算法分别晚504轮和351轮; 在200 m×200 m的网络区域中, LEACH算法和ACONC算法的第一个节点死亡轮数比在100 m×100 m的网络区域中分别提前了267轮和338轮, 而CAROCN算法的第一个节点死亡轮数仅提前68轮. 表1为不同算法在2 000轮后的存活节点数. 由表1可见: CH节点轮换次数为2 000轮时, 在100 m×100 m网络区域中, CAROCN算法的存活节点数比LEACH算法多182%, 比ACONC算法多100%; 在200 m×200 m网络区域中, CAROCN算法的存活节点数基本上无变化. 因此CAROCN算法的网络生命周期更长, 稳定性和扩展性更好. 图4 不同网络区域中各算法第一个节点的死亡轮数Fig.4 Number of death rounds of the first node of each algorithm in different network areas 表1 不同算法在2 000轮后的存活节点数 图5 100 m×100 m(A)和200 m×200 m(B)的网络区域中网络的总能耗曲线Fig.5 Total energy consumption curves of network in network areas of 100 m×100 m (A) and 200 m×200 m (B) 网络的生命周期也与网络的能耗有关, 在100 m×100 m和200 m×200 m的网络区域中, 网络的总能耗和节点的平均节点剩余能量变化分别如图5和图6所示. 由图5和图6可见, 随着网络中CH节点选择轮数的增加, 网络能耗曲线缓慢上升, 平均节点剩余能量曲线下降, 而LEACH算法和ACONC算法的网络能耗曲线比CAROCN算法下降更快. 网络中第一个节点死亡后, LEACH算法和ACONC算法的网络能耗曲线虽然缓慢减少, 但由于节点任务分配不均匀, 负荷大的节点能量很快耗尽, 网络的平均节点剩余能量仍不断减少. 在200 m×200 m的网络区域中, LEACH算法和ACONC算法中平均节点剩余能量一开始就急剧下降, 而CAROCN算法中的平均节点剩余能量虽略有下降, 但基本上与100 m×100 m的网络区域保持一致, 表明CAROCN算法比其他两种算法具有更好的可扩展性. 图6 100 m×100 m(A)和200 m×200 m(B)网络区域中平均节点剩余能量曲线Fig.6 Average node residual energy curves in network areas of 100 m×100 m (A) and 200 m×200 m (B) 图7为网络在100 m×100 m的检测区域中网络存活节点数目的变化曲线. 由图7可见, 在网络的初始工作阶段, 网络中的存活节点数目不变, 但由于LEACH算法、 ACONC算法和CAROCN算法中节点的工作负荷不同, 存活节点数在CH节点的不同轮换次数开始减少. LEACH算法和ACONC算法在出现第一个节点死亡后, 存活节点数量急剧减少, 尤其在200 m×200 m的网络区域中较明显, 但200 m×200 m的网络区域中CAROCN算法的存活节点数目与100 m×100 m的网络区域中的存活节点数目基本相同. 图7 100 m×100 m(A)和200 m×200 m(B)网络区域中存活节点数目变化曲线Fig.7 Change curves of number of surviving nodes in network areas of 100 m×100 m (A) and 200 m×200 m (B) 综上所述, 针对无线传感器网络的能效问题, 本文提出了一种CAROCN算法, 首先基于每个环中能量消耗最小原则计算出每个环的最优簇头数; 然后每个环按相应的最优簇头数分成若干不同大小的簇, 同时又单独考虑了最外环的最优簇头数, 使网络的能量消耗更均匀; 最后在簇头选择时, 考虑了每个环的最优簇头数与相应环中节点数目的比值、 当前轮次中节点的剩余能量与节点初始能量的关系以及CM节点到CH节点的最短距离, 均衡了网络的能量消耗, 延长了网络的生命周期. 仿真实验结果表明, CAROCN算法在平衡网络能耗和延长网络生命周期上比LEACH算法和ACONC算法性能更好, 且在不同规模网络中具有更好的扩展性.
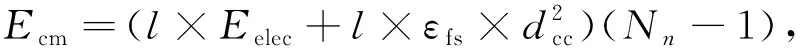



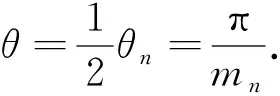
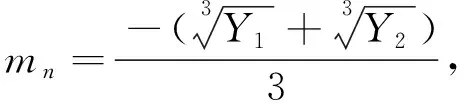

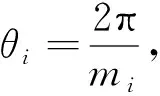




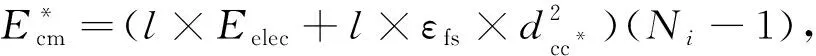





1.3 CH节点的选举

2 仿真实验分析
2.1 网络生命周期分析


2.2 网络能耗分析


2.3 存活节点数目分析

