对流-扩散方程初边值问题的重整化群方法
2020-09-27张艳妮
周 冉, 张艳妮
(1. 吉林大学 数学学院, 长春 130012; 2. 吉林建筑科技学院 基础科学部, 长春 130114)
0 引 言
重整化群方法[1]源于量子场论中电动力学的分析技巧, 由于该技巧涉及了电荷之间变换的群性质, 因而被称为重整化群方法. Wilson等[2]建立了统计力学中相变临界现象的重整化群方法, 进而促进了相变临界现象理论的发展. Chen等[3]将上述重整化群思想应用于奇异摄动问题, 提出了一套系统求解奇异摄动问题的一致有效渐近解的新方法, 即奇异摄动重整化群方法, 其主要优点在于不需要如平均化、 多尺度等方法那样预先分析所考虑问题的特殊结构而做出一些必要的先验假设, 其系统简单的求解格式可以很容易模式化地得到近似解: 从关于小参数做形式展开开始, 确定发散项, 然后通过重整化技巧去掉发散项, 得到相应的重整化群方程和近似解. 近年来, 重整化群方法广泛应用于其他不同类别的问题, 例如边界层问题[4]、 不变流形约化问题[5]、 高振荡问题[6]、 随机微分方程的摄动问题[7]和偏微分方程的摄动问题[8-9]等.
本文考虑如下对流-扩散方程的初边值问题:
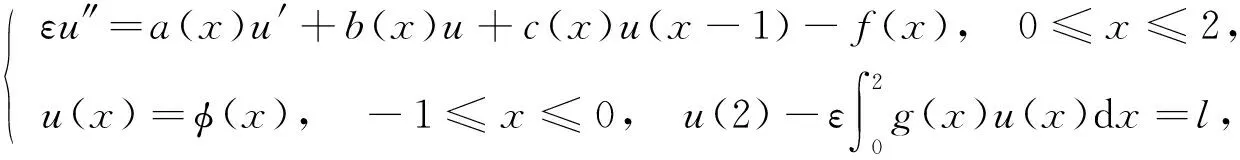
(1)
其中:ε>0是小参数;φ(x)在[-1,0]内充分光滑;a(x),b(x),c(x),f(x)和g(x)充分光滑,a(x)>0,b(x)≥0,c(x)≥0;l是常数. 对流-扩散方程是一类描述黏性流体运动的数学模型, 广泛应用于物理、 化学、 生物等许多领域[10-11]. 显然, 问题(1)的解析解很难求出. 因此, 构造其一致有效的逼近解尤为重要. 本文首先将问题(1)分解为左问题和右问题, 然后分别利用重整化群方法得到一致有效的逼近解, 最后通过光滑缝接得到原问题的一致有效逼近解.
1 主要结果
首先, 将初边值问题(1)分解为左问题:

(2)
和右问题:

(3)
从而求问题(1)的逼近解即转化为求问题(2)和(3)的逼近解.
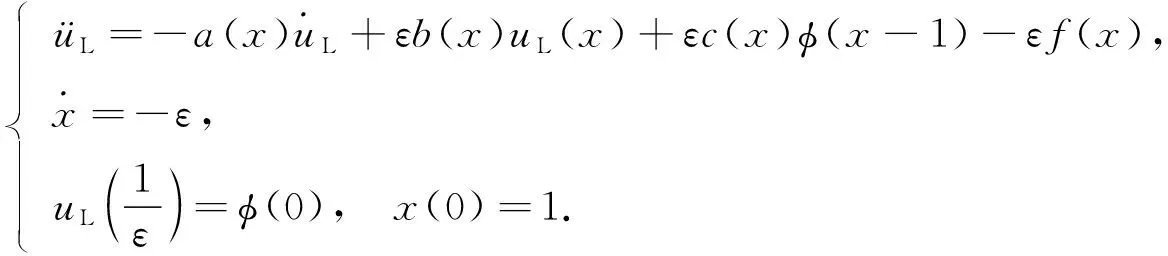
(4)
设
x=x0(t)+εx1(t)+ε2x2(t)+…,
将x和μL代入式(4), 并对比等式两端ε同次幂的系数, 得
解式(5)得

从而得到式(4)的一阶逼近解:

(7)
引入自由参数σ, 分别将式(7)中含有t和t2的项(长期项)分解为t-σ+σ和t2-σ2+σ2, 则有

(8)
下面对A,C0,C1进行重整化. 设
则式(8)变为

(9)


(10)
解方程(10)得
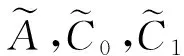


(12)
类似左问题的求解过程可得右问题(3)的一阶逼近解:


综上, 可得本文的主要结果:
定理1设φ(x)在[-1,0]上充分光滑,a(x),b(x),c(x),f(x)和g(x)充分光滑,a(x)>0,b(x)≥0,c(x)≥0, 则
是对流-扩散方程边值问题(1)的一阶一致有效逼近解, 其中:

作为应用, 考虑如下时滞微分方程初边值问题:

(14)
对应于式(1)中
的情形. 由式(11)得
由式(13)得

解得
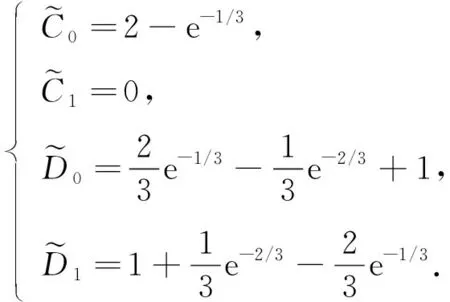
(15)
利用定理1可得式(14)的如下一阶逼近解:

