外场作用下缀饰原子的双光子阻塞

刘佳佳, 朱红波

(东北师范大学 物理学院, 长春 130024)

在多光子-物质相互作用的跃迁过程中, 会发生当有一个光子通过或被物质吸收时, 其他光子可能被吸收或反射, 该现象即为光子阻塞效应. 光子阻塞最早在单原子-单模腔耦合系统中被证实[1-2]. 本征能量谱中参量的非线性行为是发生光子阻塞效应最重要的前提条件[3], 这种非线性使初始制备低激发态间的共振在之后向高能级跃迁的过程中移位, 第二个光子及其后的光子可能远离共振作用, 即使可导致能级间跃迁也是几率很小的高阶效应, 即第二个光子及其后光子的吸收被阻塞了. 在一些量子系统中已经实现光子阻塞, 如真空腔和二能级系统间的强相互作用引起的非线性可导致光子阻塞[4], 在量子电动力学(QED)和光学系统中的理论研究结果较多[5-9].

目前, 对光子阻塞的研究已从双光子推广到多光子阻塞. 当腔中有一个光子时, 在一定的相互作用条件下, 第二和第三个光子分别通过双光子和三光子过程被吸收. 这种多光子阻塞可产生多光子流及理想纠缠光子源等. 近年来, 人们应用不同的物理机制与模型对多光子阻塞进行了研究[10-12]. 本文选择外加一个经典驱动场的Jaynes-Cummings(J-C)模型, 对单原子-腔系统在缀饰态空间进行描述, 并分析其动力学跃迁特性. 用主方程方法及Fröhlich变换, 得到系统的有效Hamilton量, 进而求出二阶关联函数, 并对双光子阻塞过程及反聚束效应进行理论分析.

1 单原子-腔QED中的多光子共振

用主方程方法处理单原子-腔QED模型, 其中原子与腔共振频率为ω0. 经典场作用下的J-C模型Hamilton量为

(1)

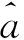
其中:κ为腔场衰变率；γ为原子衰变率. 令γ=2κ, 则体系基态为

|G〉=|ψ(0)〉=|0,g〉,

(3)

原子和腔场共振的缀饰态为

|ψ±(n)〉=2-1/2(|g,n〉±|e,n-1〉),

(4)

对应的能级(令ħ=1)为

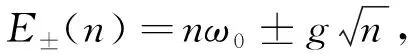
(5)

从缀饰态能级可得多光子共振条件为

(6)

2 双光子过程的有效动力学

下面给出一个简单模型, 对体系的Hilbert态空间进行有效截断, 即截取|ψ+(1)〉～|ψ-(4)〉6个缀饰态能级, 并分析该截断部分的双光子跃迁过程. 在6个能级模型中, |ψ-(2)〉和|ψ+(2)〉能级对|ψ+(1)〉和|ψ-(3)〉的共振和跃迁过程影响较大, 其为双光子跃迁的中间态, 可能会被绝热消除. 用主方程方法计算系统的有效Hamilton量, 并分析高阶能级对能级移位的影响.

2个能级|ψ+(1)〉和|ψ-(3)〉共振时满足

(7)

6个能级|ψ+(1)〉～|ψ-(4)〉的表达式分别为

为求得体系主方程, 需重新定义体系的产生湮灭算符, 用久期近似并绝热消除中间态, 即可得体系主方程为

其中Λ～Λj为缀饰态迁移率. 当定义腔场和原子的衰减率分别为γ和к时, 计算求得各迁移率分别为

|ψ+(1)〉和|ψ-(3)〉间的跃迁耦合系数为

(15)

当经典光场与某特定缀饰态发生共振时, J-C模型的非线性可导致失谐. 考虑高能级的影响, 可得各缀饰态的能级频率移位分别为

其中:L和U分别表示缀饰态能级对中的较低和较高能级, 如3U指代|ψ+(3)〉； 下角标0～9分别表示10个能级|ψ(0)〉～|ψ-(5)〉. 从而体系的有效Hamilton量为

3 双光子过程的二阶关联函数

用光学相干量子理论可解释独立热光源间的关联, 将相干光理论及其描述推广到含有多原子的相互作用系统中, 对原子相干性进行研究, 可得多个光源相干性的特征函数为一阶关联函数或高阶关联函数. 如杨氏双缝干涉实验中的双缝可视为2个光源, 用其电场强度描述干涉条纹可得一阶关联函数, 即杨氏双缝实验中观察到的图像为一阶干涉条纹. 由于任意点干涉条纹的强度表达式为2个电场强度的乘积, 因此一阶关联函数可描述光场振幅间的关联. 二阶关联函数的表达式为4个电场强度的乘积, 即二阶关联函数描述光场强度间的关联. 更高阶的关联函数以此类推. 由于相干光或处于相干态的光场均存在任意关联函数, 因此将其定义为相干态, 即关联函数是描述光场统计特性的一种重要方法. 当单原子-单模腔场系统受一个经典光场作用时, 经典场与系统的某特定缀饰态共振, 非线性引起的失谐会导致对其他光子产生阻塞效应[1]. 光子阻塞的一个明显结果是二阶关联函数呈反聚束效应. 在共振跃迁过程中, 由于受原子与腔场间的相互作用强度、 经典场的驱动强度等因素影响, 因此聚束和反聚束效应均可能发生.

下面用主方程方法求解该六态模型的光子二阶关联函数g(2)(τ). 在不同驱动强度下, 判断g(2)(0)的大小, 当g(2)(0)>1时为聚束效应, 当g(2)(0)<1时为反聚束效应. 在调制系统各参量的条件下, 当二阶关联函数出现反聚束行为时, 即发生了光子阻塞.

将主方程(14)展开, 则空腔发散的光子二阶关联函数为

g(2)(τ)=1+χe-3γ|τ|+αe-2γ|τ|cos(ντ)+e-2γ|τ|[βcos(2Ωτ)+ζsin(2Ω|τ|)],

(25)

其中各系数分别为

图1 当κ=0.1, γ=2κ, ε=100κ, g=300κ时的光子二阶关联函数Fig.1 Second-order correlation function of photon at κ=0.1, γ=2κ, ε=100κ, g=300κ

当给定不同参数(外场驱动强度、 偶极耦合强度)时, 二阶关联函数g(2)(τ)分别如图1和图2所示. 当外场驱动强度ε=100κ、 偶极耦合强度g=300κ时, 由图1(A)可见,g(2)(0)<1, 双光子高阶跃迁过程呈明显的反聚束效应, 即发生了光子阻塞现象. 当保持耦合强度不变, 改变外场驱动强度, 使ε=40κ时, 由图2(A)可见,g(2)(0)=2.30>1, 双光子高阶跃迁过程呈明显的聚束效应. 表明聚束和反聚束效应在双光子共振时均会发生, 关键取决于驱动强度的大小. 由图1(B)和图2(B)可见, 当选取较长的时间段后, 在不同驱动强度下, 两个关联函数图像的振荡趋势基本相同, 在15 s后稳定于g(2)(τ)=1处.

图2 当κ=0.1, γ=2κ, ε=40κ, g=300κ时的光子二阶关联函数Fig.2 Second-order correlation function of photon at κ=0.1, γ=2κ, ε=40κ, g=300κ