港池长周期波浪振荡模态研究

2020-09-27刘远超袁博博

水道港口 2020年4期

刘远超,袁博博,于倩

(1.河海大学港口海岸与近海工程学院，南京 210098； 2.中国港湾工程有限责任公司，北京 100027； 3.华北水利水电大学环境与市政工程学院，郑州 450046)

在港口的建设中，往往修建防波堤对港域水体进行掩护。然而当外海波浪周期较长时，其掩护效果并不直观。并且当外海长周期波浪的频率与港口自身固有频率比较接近时，港域水体易发生强迫振动，港域波高幅值将剧烈上升，其振幅可达到入射波浪振幅的数倍，从而发生港口共振[1]，进而危害港域泊稳条件。

20世纪50年代开普敦港口发生严重的假潮振荡事故，国外学者开始针对港口的长波和假潮开展研究。Botes[2]等人根据南非港口20世纪70年代末和20世纪80年代初的数据，对长波的起源和产生机制进行研究，并根据经验得出长波与热带气旋之间的关系。Hwang和Tuck[3]通过求解奇异积分方程，研究了恒定水深任意形状与尺度港口的港池振荡。Heneik[4]等人利用物理模型试验模拟贝鲁特港内波浪分布及破碎情况，并用非线性Boussinesq模型研究港内长波增长及空间变化，结果发现物理模型与数值模型结果吻合良好，港内长波能量主要集中在50～80 s和6～7 min，二者分别对应于港池的自然模态和赫尔姆霍茨模态，该方法可为后续风浪和涌浪作用下的港池低频振荡研究提供参考。Duncan Stuart[5]基于恩瓜拉港(Port of Ngqura)船舶剧烈运动和系泊事故，基于实测数据和MIKE21-BW模型研究了港内长波的产生、侵入和共振现象。王岗[6]基于线性假定，给出了狭长矩形港湾纵向振荡的解析表达。史力生和潘军宁[7]基于滨海核电站取水口工程的波浪整体模型试验，分析了取水明渠内长周期波动产生的条件及影响因素。马小舟、刘嫔[8-9]等人采用Boussinesq波浪数值模型模拟了孤立波，模拟了不同波高的孤立波分别对常水深和变水深细长港作用时港内的响应。史宏达、徐国栋[10-11]等人利用Boussinesq波浪数值模型针对理想地形下的港池不同入射波周期的港内波高进行计算，预测港内振荡的发生，进而提出预防措施。冯海暴[12]、乔吉平[13]等人结合实测资料，研究了长周期波作用下港域长周期波浪分布规律和打桩船作业存在的问题，并提出相应的防治措施。尽管很多学者针对长周期波浪开展了研究，但是很多研究尚停留在特定理想港池的长波振荡情况，因此本文采用数值模拟方法，研究某核电港域的长周期波浪振荡频率，并对港内长周期波浪的振荡模态进行了分析。

1 模型验证

1.1 模型简介

MIKE21-BW波浪数值模拟模型由丹麦水利研究所开发，该模型基于Madsen和Sørensen[14-15]提出的改进频散关系和变浅性能的Boussinesq方程，采用交替方向隐格式(ADI)进行时域内的求解。经过长期发展，BW模型不仅可以较好地描述近岸水域波浪传播过程中发生的折射、绕射、反射和非线性波-波相互作用，而且还可以推广至研究破碎区和上爬区的波浪现象。其控制方程和数值计算方法可参见文献[14-15]。

1.2 模型验证

本文结合某核电厂局部波浪整体物理模型试验，验证数值模型的合理性，图1和表1分别为试验中模型布置图和波浪要素，测点具体布置参见图2。核电厂海工工程规划方案的平面布置包括取水明渠、排水明渠、大件码头、护岸和干施工围堰，各分项工程平面规划方案如下：取水明渠由南北两条取水堤环抱而成，口门朝向NNE，两堤堤头相距240 m，取水南堤堤顶高程为12 m。排水明渠分两期建设，其中一期工程包括东西两条排水堤，口门朝向SSE，两堤堤头相距190 m，排水东堤高程为11 m。北部护岸挡浪墙顶高程为16 m。SE和SSE方向参见图1。

表1 试验波要素Tab.1 Wave element in physical model test

物理模型试验在40 m×60 m×1.5 m的波浪港池中进行，港池一端装有多向不规则波造波机系统，可按要求模拟规则波和各种谱型的不规则波，港池四周装有消浪设施以减小波浪的二次反射，波高采用DJ-800型多功能数据采集、处理及分析，实验比尺为1：80。

数值模型完全参照物理模型平面布置(图1)设定，将物理模型试验的平面布置以及试验水池按照试验比尺1：80进行同比放大，得到港域地形数值模型图。波浪数学模型的计算范围是1 600 m×5 000 m，地形设置与物理模型完全相同，即港外高程-11 m、港内高程-9 m，模型的空间步长采用10 m。波浪完全采用物理模型试验的波要素，按试验比尺1：80同比放大后，生成造波文件，输入到造波线，波浪的时间步长和模拟时间与物理模型试验一致。为确保波浪传播稳定，对模型两侧固壁边界采用全反射。由于港域所有防波堤型式均是斜坡式结构，扭王字块进行护岸，采用部分反射，从而较好地模拟扭王字块的消波作用。由于模型主要模拟港域的长周期波浪振荡情况，故而在海绵层的设置中注重吸收长周期波浪。在模型的开边界海绵层的厚度均设置了100层，即海绵层的厚度达到1 000 m，从而最大程度吸收长周期波浪。

图1 模型布置图图2 测点布置图Fig.1 The model layout Fig.2 The measuring point layout

由于本文的研究重点是长周期波浪，因此着重验证MIKE21-BW模型对长周期波浪的模拟情况，分别对港池内长周期波浪的波高与周期进行验证。利用傅立叶变换进行滤波处理，低通滤波器的截止频率为0.033 Hz(对应波浪周期为30 s)，即30 s以上的波浪定义为长周期波浪。

1.2.1 波浪波高验证

利用傅立叶变换分离长周期波浪序列，将长周期波浪的有效波高与物理模型试验中的长周期波浪有效波高进行对比，得到如图3所示港域测点数值模型与物理模型波高对比图。可见，各测点总波高和长周期波高数值模拟结果和物理模型试验结果吻合度较高，总体验证结果良好。

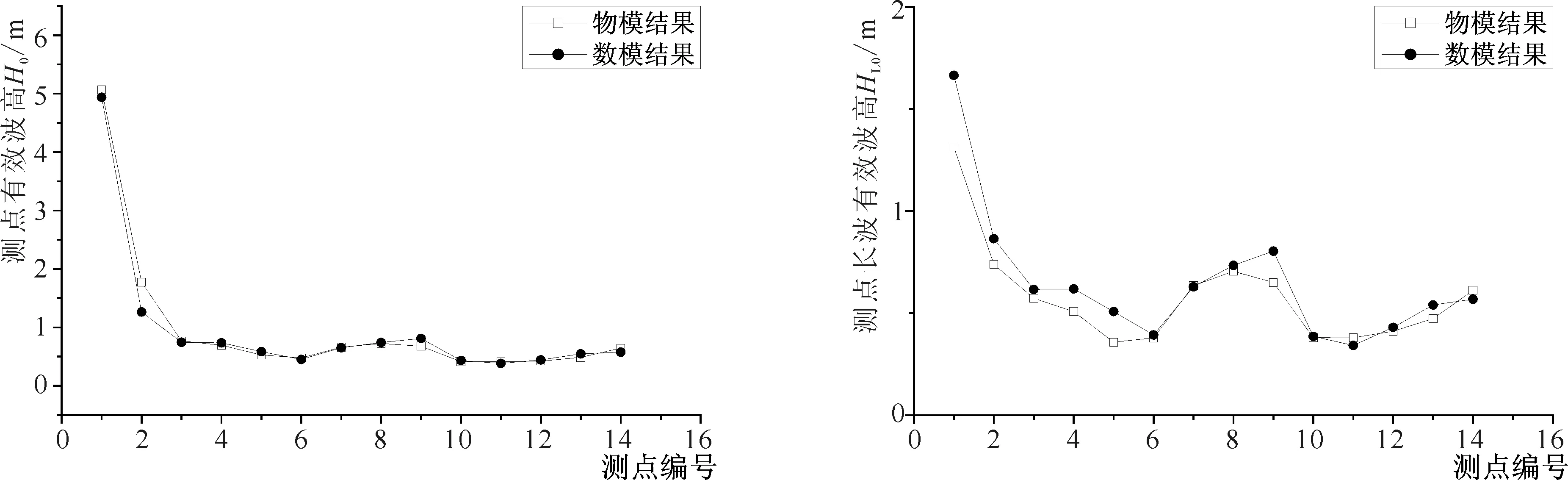
3-a 入射波向SE，HS=5.15 m

1.2.2 波浪周期验证

利用傅立叶变换分离出各测点的长周期波浪，统计长周期波浪的振幅频率图，其对比结果参见图4。鉴于测点数量较多，本文选取8和13两个典型测点的波浪进行对比。在各组工况下，港内各测点波浪周期的数值模拟结果和物理模型试验结果吻合度较高，总体验证结果良好，即数值模拟计算结果可以较好模拟港池长周期波浪振荡情况。

4-a 入射波向SE，HS=5.15 m

2 港池的固有频率

为进一步了解港池的共振模态和对应频率，本文采用白噪声进行研究。本文白噪声的时间序列共模拟10 000 s，时间步长取0.1 s。入射波向为SE向，波浪以单向波的形式传入港域，各个频率下波浪的振幅均为0.000 5 m。计算结果统计不同测点的波面时间过程，将30 s以上的波浪定义为长周期波浪，对应频率为0.001～0.033 Hz。

图5展示了港内测点和入射白噪声波序列的幅频对比图，在港内选取特征点9和14进行对比分析。在白噪声波序列的作用下，港池发生了明显的长周期振荡，港内测点9在600～850 s、250～320 s、130～170 s、66～72 s、53～55 s所对应的频率下均发生了明显的港湾共振，在600～850 s的长周期波浪振荡幅度为0.002 4 m，达到入射波浪振幅的5倍。测点14在600～850 s、250～320 s、130～170 s、77～80 s、36～39 s所对应的频率下均发生了明显的港湾共振。在600～850 s的长周期波浪振荡幅度为0.003 3 m，达到入射波浪振幅的6.6倍。由于测点9和14在600～850 s、250～320 s、 130～170 s区间均发生明显的波能放大现象，因此该部分区间对应于港池的固有频率。而在测点9出现了66～72 s、53～55 s的长周期波浪振荡，测点14出现了77～80 s、36～39 s的长周期波浪振荡，这可能是由于港池的不规则导致，属于港池内部的局部长波振荡。

图5 白噪声诱导下长波振幅频率图Fig.5 The long-period wave amplitude-frequency under white noise

3 港池长波振荡模态

根据白噪声的探测结果，可以找到港池长周期振荡的频率区间以及放大倍数，然而对于港池的固有频率的具体值和长周期波浪振荡模态尚不清晰，因此本文设置一系列规则波，研究各个规则波作用下港池的长周期振荡模态，入射波向采用SSE向，规则波的波高均设置0.01 m，周期取值采用白噪声计算结果中发生长周期振荡的对应区间，即600～850 s、250～320 s、130～170 s对应区间。

3.1 600～850 s波浪振荡模态

入射波要素采用600～850 s区间内的一系列规则波，计算时长取80 000 s，探测长周期波浪振荡的最大幅值，从而锁定港池固有频率。在830 s附近时港池长周期振荡波高显著，对830 s附近周期进行局部加密后输入到模型中，发现833 s的长周期波浪计算结果最大，因此833 s对应于港池的固有频率。在833 s的长周期规则波作用下，港内波高明显被放大，最大波高达到0.053 m，超过入射波高的5倍，计算结果见图6。根据图6-a的计算结果，从港池左侧取水口到港池外部口门，即图中的A-B断面，波浪的波面高度逐渐减小，即833 s长周期波浪振荡模式是以口门B为波节，港域内部边界A为波腹的长周期振荡，此时长周期波浪的1/4波长与港域的尺度相当，该振荡模式称为Helmholtz模式。该模式引起的波浪振幅放大幅度最为剧烈，为港池振荡的第一模态。

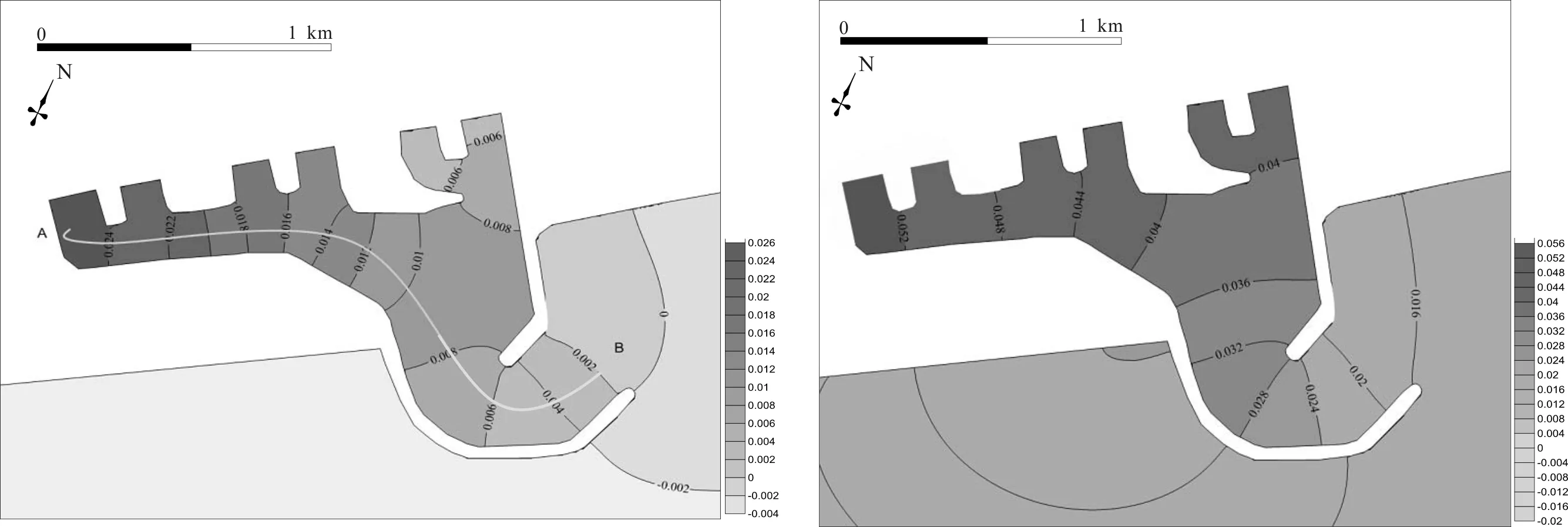
6-a t=40 000 s波面高度 6-b 港内波高计算结果

3.2 250～320 s波浪振荡模态

在250～320 s区间内设置一系列周期的波浪输入到模型中，计算时长为30 000 s，发现在300 s时港内的长周期波浪振荡尤为显著，因此300 s对应于港池的固有频率。计算结果见图7，可以看到港内波高明显被放大，最大波高达到0.046 m，达到入射波高的4.6倍。根据图7-a的计算结果，从港池左侧取水口到港池右部边界，即图中的A-B断面，A处波面位于最高位置时，B处波面位于最低位置，A、B两处均是波腹，即波浪的振荡模式是以港池内部A和B为波腹，C处为波节的长周期振荡，此时长周期波浪的1/2波长与港域的横向尺度AB相当，其对应于港池长周期波浪振荡的第二模态。

7-a t=18 000 s波面高度 7-b 港内波高计算结果

3.3 130～160 s波浪振荡模态

入射波要素采用130～160 s区间内的一系列规则波，计算时长取30 000 s，探测长周期波浪振荡的最大幅值，从而锁定港池固有频率。在150 s附近时港池长周期振荡波高显著，对150 s附近周期进行局部加密后输入到模型中，发现151 s的长周期波浪计算结果最大，因此151 s对应于港池的固有频率。计算结果参见图8，港内左侧取水口A处和中部取水口C处波高均明显被放大，最大波高分别达到0.045 m和0.046 m，达到入射波高的4.5倍和4.6倍。根据图8-a的计算结果，从港池左侧取水口到港池右侧，即图中的A-B断面， A处波面位于最低位置时，D处波面正好处于水平位置，C处波面正好位于最高位置，港池右侧B处波面位于水平位置，其振荡模式是以港池内部A和C为波腹，B和D为波节的长周期振荡，此时长周期波浪的3/4波长与港域的横向尺度AB相当，对应于港池第三模态。