借助几何画板，对2017年全国2卷20题的思考

雒晓雅 吴帝春

[摘  要] 文章以2017年全国2卷第20题第（2）问为载体，以几何画板为探究工具，展现了思考此题的思维过程，旨在从几何角度寻求该定点的位置，在探究过程中意外找到了高等几何背景下极点极线的“配极原则”与此题的联系.

[关键词] 几何角度;极点极线;配极原则

圆锥曲线中极点极线的定义

已知圆锥曲线C：Ax2+Cy2+2Dx+2Ey+F=0（A2+C2≠0），则称点P（x0，y0）和直线l：Ax0x+Cy0y+D（x0+x）+E（y0+y）+F=0是圆锥曲线C的一对极点极线.

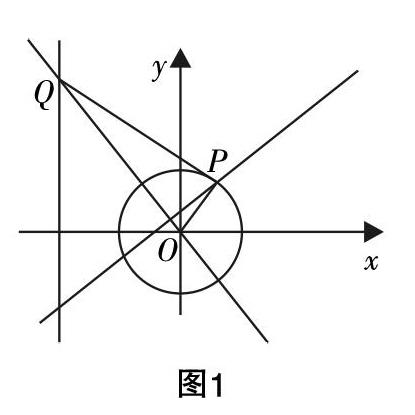
引例：（2017年全国2卷（理），20题）设O为坐标原点，动点M在椭圆C：■+y2=1上，过M作x轴的垂线，垂足为N，点P满足■=■■.

（1）求点P的轨迹方程;

（2）设点Q在直线x=-3上，且■·■=1，证明：过点P且垂直于OQ的直线l过C的左焦点F.

由（1）知，点P在圆x2+y2=2上运动，而点Q在直线x=-3上，即已知点Q的横坐标为-3，且满足■·■=1，则一个点P决定一个点Q的位置，即决定点Q的纵坐标，由此决定了垂线l的位置. 观察几何画板动态的过程，随着点P的运动，点Q随之运动，直线l随之运动，但在运动过程中，动直线l恒过一定点. 通过这样的分析，可知，决定定点位置的要素有：圆、直线x=-3及向量数量积■·■=1，因此，如果改变这些值的大小，尽管会改变点的位置，但很可能不会改变直线l恒过定点的事实. 本文怀揣着这样的猜想，旨在探寻该定点的几何意义.

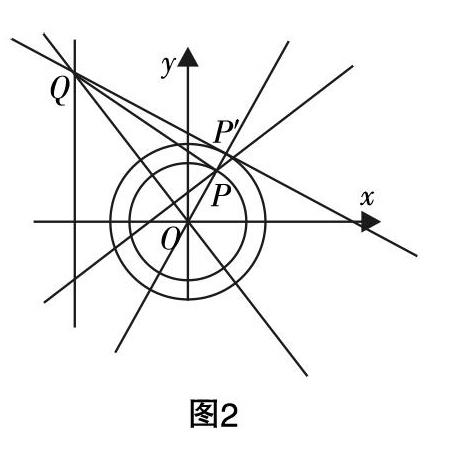
首先，若要从几何角度考虑，需要考察数量积■·■=1的几何意义，在点P运动过程中，■为定值■，因此“点Q满足■·■=1”可以等价表述为“点Q满足■在■方向上的投影为■”，因此，过点Q作直线OP的垂线，设垂足为P′，满足OP′=■OP，在这里，改变■·■的值，将影响点P′的位置，（例如，当■·■=-1时，P′在直线OP上，且满足■=■■;当■·■=0时，P′和点P重合），无论数量积为何值，点P′的轨迹为圆，圆心O2为（O2与O重合），于是点Q为“圆O2在点P′处的切线与直线x=-3的交点”.

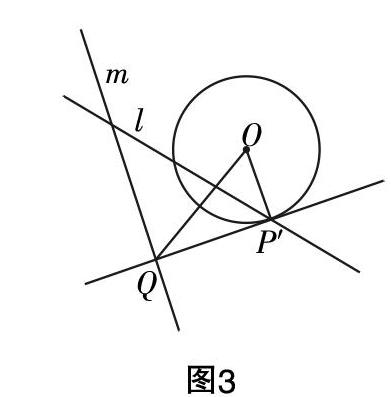
要寻找几何意义，就得脱离直角坐标系，来观察这个动态过程，不妨绕过点P，从P′点出发，有如图3所示的几何问题：

点P′为圆O上任意一点，过点P′作圆O的切线，交定直线m于点Q，过点P′作直线OQ的垂线，记作l，证明：直线l恒过一定點.

显然，对于定圆来说，直线m的位置影响着该定点的位置，于是笔者开始探索直线m的位置与待求定点的关系.

不妨先按照特殊情况来研究，当定直线m与圆O相切时，如图4所示，显然能够得出动直线l恒过定点，该定点为定直线m与圆O的切点.

而借助几何画板，发现当定直线m与圆O相交时，待求定点在圆外;当定直线m与圆O相离时，待求定点在圆内，这不禁让人联想到极点极线的配极原则.于是大胆猜想，待求的定点即为直线m在圆O上所对应的极点.

证明：如图4，5，6所示，设直线m所对应的极点为M，只需证明在三种情形下，均有P′M⊥OQ即可.

此时笔者发现自己绕了很大的一个圈子，无论直线m与圆O的位置关系如何，题意中“过点P′作直线OQ的垂线”，即意味着过点P′作点Q对圆O的极线，根据配极原则，若点Q恒在直线m上，则点Q所对应的极线恒过定点，记为M′，并且该定点M′即为直线m所对应的极点.

结论：综合以上分析，数量积■·■影响着圆O2的半径，或者说点P′的位置;待求定点M′即为直线m在圆O2上所对应的极点.

利用这道题目的数据来解释以上原理，由于■·■=1，可构造圆心在原点O，半径为■的圆，作圆O在点P′处的切线与直线x=-3的交点，记为点Q. 根据极点极线的定义，“过点P′作OQ的垂线”即为“过点P′作点Q所对应的极线”. 由于点Q恒在直线x=-3上，则它所对应的极线恒过定点，而题意中要求的是“过点P作OQ的垂线”，即“过点P作点Q所对应极线的平行线. 由于极线恒过定点，那么它的平行线也恒过另一个定点.”

接下来考虑两个定点之间的位置关系：

我们来考虑下面几何模型：当直线l1恒过定点1（M′）时，当点P′（或点P）绕着圆心运动，l1的平行线l2必然恒过定点M，且满足定点1（M′）、定点2（M）及圆心三点共线，并有比例关系■=■.

现在根据上面的分析，来叙述一下本题中第（2）问定点（-1，0）的产生过程：在此题中，点P为圆x2+y2=2上任一点，由于满足■·■=1，导致垂足点P′在圆x2+y2=■上运动，而直线x=-3关于圆x2+y2=■的极点为-■，0，即为定点1（M′）. 由于■=■，可推出定点2（M）坐标为（-1，0）.

通过以上分析，了解了题意中各个条件之间的关系，笔者有了以下几道改编题供大家思考：

（1）设点Q在直线x=-1上，且■·■=0，证明：过点P且垂直于OQ的直线l恒过定点.

（2）设椭圆C的左焦点为F，过原点O作直线PF的垂线l，作点P处的切线交直线l于点Q，问：是否存在定直线，使得点Q在该直线上，若存在，请求出直线方程;若不存在，请说明理由.

（3）设椭圆C的左焦点为F，过原点O作直线PF的垂线l，点Q在垂线l上，且满足■·■=1，证明：点Q恒在直线x=-3上.