例谈回避分类讨论的六大策略

张魁

[摘  要] 分类讨论是常见而重要的一种解题策略，它较好地体现了对“能力”的考查，备受命题者的关注，是当下高考热点问题.当然，分类讨论需做到不重复、不遗漏，这就对思维的严谨性提出了较高的要求，学生时常会因为考虑不全面而导致解题失误. 从优化解题过程，提高解题效率的角度来思考，有些问题可简化或避免分类讨论.文章对此进行一些归纳探究.

[关键词] 高中数学;分类讨论;回避;策略

正确灵活地运用数学思想，不仅可以达到化难为易的解题效果，还可以有效提升解题的大局思路与总体思考能力. 分类讨论是一种行之有效的思想方法，也是一种重要的解题策略，其重要性在近几年的高考试题中也有明显体现.通过合理分类可以分化问题，化零为整，一一击破难点问题，在讨论时需做到不重不漏，而这在一定程度上也对学生的数学思维提出了较高的要求. 事实上，分类讨论并不是所有问题都可适用，有些题型浅显观察似含有分类因素，但当对问题本质深入观察和细致分析之后，又可避免繁杂的讨论过程.因此，我们在关注分类讨论思想应用的基础上，也需克服动辄讨论的思维定式，不可盲目而呆板地进行分类讨论，而应充分挖掘潜在的特殊因素，灵活机动地运用适当的策略，从而简化或回避分类讨论.

引参换元，规避讨论

换元法是将某个式子视为一个整体，引入新的变量，从而将问题转移到对一个新对象的研究中去，使问题得到简化. 当我们以一个新字母替换题目中的整体时，则可以规避分类讨论的繁杂过程，给人以柳暗花明的感觉，从而使问题迎刃而解.

例1：当a>0时，解关于x的不等式■>a-2x.

分析：本题若先平方，则需进行分类讨论从而获解，过程烦琐.而通过换元法令■=t，可避免讨论，简化解题过程.

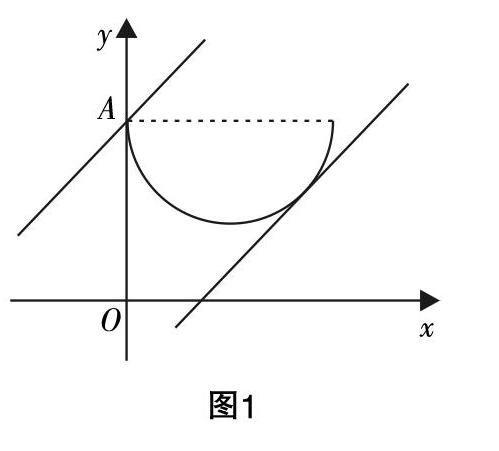
解：令■=t，则t≥0，且有x=a-■. ？摇代入原不等式，据条件a>0，可化简得2t2-at-a2<0，所以-■

■参数分离，避繁就简

例2：设函数f（x）=x2-1，对于任意x∈■，+∞，f■-4m2f（x）≤f（x-1）+4f（m）恒成立，试求出实数m的取值范围.

分析：此例题若直接进行求解，需经历多种情况的讨论来解决，过程烦琐不说，难度也较大，学生极易思维卡壳，造成错误.事实上，可以分离参数，解题的关键是将原问题完美转化为具体函数的求最值问题，从而提高解题的速度和正确率.

解：据题意，可得■-1-4m2（x2-1）≤（x-1）2-1+4（m2-1），即■-4m2≤-■-■+1在x∈■，+∞上恒成立.

令f（x）=-■-■+1，x∈■，+∞，则当x=■时，f（x）可取到最小值，最小值为-■.

所以■-4m2≤-■，可解得m∈-∞，-■∪■，+∞.

整体思想，免于讨论

所谓整体思想，望文生义就是将若干式子组合为一个整体，直接或是变形后可代入另一个式子，从而减少或回避求解单个变量而导致的烦琐运算，使解题过程简捷明快，而且富有创造性. 事实上，在解决一些数学问题时，若能从全局着眼深入观察特征和本质，则可以免于讨论，收到事半功倍的效果.

例3：试求出同时满足以下两个条件的所有复数z，①z+■∈R，且1

分析：按常规解题思路，先设z=a+bi（a，b∈R），然后再讨论求解，会导致题目变得复杂，学生在计算过程中也較易出错.这时若从整体思想入手，将z+■视为一个整体，然后化归为一元二次方程求根，则可以有效回避讨论，使复杂的题目变得简单，从而快速、准确地得出结论.

解：设z+■=a，则有z2-az+10=0，又有1

数形结合，避免讨论

数形结合是极具数学特色的信息转化，在解题中，它呈现各种独特优势，如思路上的灵活，过程上的便捷，方法上的多样等，不仅有效避免了讨论，还为学生的解题提供多向通道.

例4：若直线y=x+b和曲线y=3-■有公共点，试求出b的取值范围.

分析：对于本题，若运用一般解法将函数图像的交点个数转化为判断方程解的个数，则需分类讨论x的取值范围，比较冗长，造成解题过程的混乱，此时结合图形考虑，便可以避免这一点.

解：据y=3-■，可得（x-2）2+（y-3）2=4（y≤3），那么函数所对图像则为一个下半圆，该半圆以（2，3）为圆心，2为半径，且与y轴切点为A（0，3）. 当直线y=x+b经过点A（0，3）时，b=3;当直线与该半圆相切时，■=2，解得b=1-2■或b=1+2■（舍去），再根据图1进行分析，可得1-2■≤b≤3.

正难则反，另辟蹊径

在数学解题中，一般思维是正面的、顺向的，但有些数学问题从正面着手难以完成，则不妨进行逆向思考，另辟蹊径，这就是“正难则反”策略. 在解题过程中，有一些数学问题在分类讨论过程中相当麻烦，但若用补集的方法从结论的反面进行分析和探究，从而得出反面结论，再与集合性质相结合，则可以突破思维定式，使问题化难为易，让思维进入高一阶的境界.

例5：已知三条抛物线y=x2+4ax-4a+3，y=x2+（a-1）x+a2，y=x2+2ax-2a中至少有一条与x轴有交点，求a的取值范围.

分析：本题如果从正面直接求解，则需分类讨论的情形有七种之多，繁杂程度可以想象，若运用“正难则反”策略，去掉不合题意的解集，从问题的反面“3条抛物线都不与x轴相交”这一种情况着手解决，相对于命题本身更简单、更明确，从而使问题简化.

解：当3条抛物线都不与x轴相交时，有16a2+4（4a-3）<0，（a-1）2-4a2<0，4a2+8a<0.解得-■

再排除掉以上3条抛物线都不与x轴相交的情况，取其补集，可得a≤-■或a≥-1.

反客为主，去除讨论

所谓“反客为主”，就是当从处于“主位”的对象入手难以解决时，巧妙地更换对象，将处于“客位”的对象置于“主位”，从而形成解决问题的策略，从而避免了讨论的过程，使问题得到简化解决.

例6：对于任意m∈[-2，2]，函数f（x）=mx2-mx+m-6的值总小于0，试求出x的取值范围.

分析：本题关于x的二次函数f（x）的值总小于0，即f（x）的最大值小于0，而f（x）的最大值是由x的取值范围来确定的. 如果单纯从二次函数角度去思考，问题难度系数很大，分类情形也难以定夺. 若是能考虑到函数f（x）中的x为自变量，它占据“主位”，而m为待定常数，即置于“客位”，逆转这两个对象的角色，反客为主，将f（x）视为g（m）=（x2-x+1）m-6，也就是看作关于m的一次函数，则可以回避讨论，解题过程由此得到优化.

解：设g（m）=（x2-x+1）m-6，则函数g（m）<0在m∈[-2，2]时恒成立.

因为g（m）为m的一次函数，所以只需g（-2）<0，g（2）<0.

即-2（x2-x+1）-6<0，2（x2-x+1）-6<0，所以x∈（-1，2）.

总之，当今的数学命题，无论是能力立意，还是知识立意，都彰显出对数学思想方法应用能力的一种考查. 在上述多个例题中可以看出，一些分类讨论问题可以消除或避开引起分类讨论的因素，使题目产生易解的变因素，从而简化解题过程. 由于高考题型千变万化，上述例题并不一定全面，还需学生在平时的训练中多多积累，本文旨在抛砖引玉，以期引起大家的思考，在解题中挖掘数学的魅力.