论数形结合思想在高中数学解题中的优势与应用

朱强

[摘  要] 宏观看待高中数学内容，我们发现尽管不少知识间存在着必然联系，但大多数知识具有抽象和难懂的本质特征，学生在理解的过程中仍存在着些许难度. 数形结合思想在高中数学中的优势不仅仅局限于可以帮助学生理清知识内容，最大的优势在于可以为学生打开解题思路，提高学生的思维能力. 文章从三角问题、与方程的解有关的问题、复数问题以及解析几何问题方面着手，谈谈数形结合思想在高中数学解题中的优势与应用.

[关键词] 高中数学;数形结合;思想方法;解题;思维能力

数学思想是数学能力和数学意识形成的“催化剂”，更是灵活地应用数学知识技能的源泉.高考中，几乎每个“把关题”都离不开数学思想的参与. 因此，教师需要在解题教学中引领学生时时总结、常常反思，在解題的过程中不断提炼“精髓”，使数学思想自然形成，使学生的数学解题能力在数学思想的浸润下逐渐提升.

数形结合是一种独具特色的信息转化思想，它也是解决数学问题的一个有效工具，将这一方法应用于高中数学的学习，能将直观图形和抽象数学有机地串联起来，这样的处理能够使学生的数学感知与数学思维相融合，使学生的思维过程简化，从而达到提高解题效率的目的. 下面笔者就从学生解题的角度着手，探讨以下数形结合思想的应用.

关注数形结合在三角函数中的应用

纵观历年高考试卷，三角函数是高考的热点问题，是高等数学学习和应用技术学科类的基石，也是解决实际生产问题的依据，突破这一重要知识的思想方法有很多，数形结合思想就是其中之一. 这就要求教师在解题教学中以此作为处理三角问题的重要思想方法，从而达到优化解题途径的目的.

例1：设函数f（x）的图像与直线x=a，x=b及x轴三者所构图形的面积是函数f（x）在[a，b]上的面积，已知函数y=sinnx在0，■上的面积为■（n∈N*）.

（1）试求出y=sin3x在0，■上的面积.

（2）试求出y=sin（3x-π）+1在■，■上的面积.

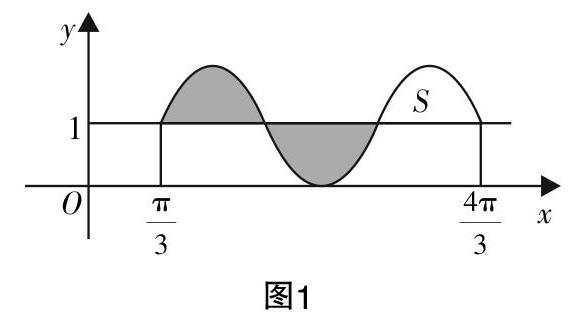
分析：需由本题中的条件“函数y=sinnx在0，■上的面积为■（n∈N*）”类比y=sin3x在0，■上的面积和y=sin（3x-π）+1在■，■上的面积来解决本题. 那么，此处则需从题设中的面积定义和所给出的函数面积出发，以此找寻相似性.而考虑这里的已知条件，尤其需关注此处条件所给出的是半个周期的面积，而很显然，第（1）问中n=3时，一个周期面积为■;而第（2）问是求由y=sin3x平移和翻转后y=sin（3x-π）+1一个半周期的面积. 如图1，画出y=sin（3x-π）+1在■，■的图像即可得出答案π+■.

评注：笔者认为，在利用数形结合解决三角问题的过程中，画图和读图是最关键的两步，先根据函数解析式画出符合要求的图像，再以形助数即可在解决问题的时候做到游刃有余. 值得注意的是，在绘制图像时，需准确反映图像中的相应数量关系，这样既能培养学生的动手操作能力，还能简化求解过程.

关注数形结合在与方程的解有关问题中的应用

在解题中，巧妙地通过数形结合这个载体来将方程的解的问题转化为曲线的交点问题，深刻挖掘出数形结合的价值，旨在简化问题的解决策略，意在培养学生应用意识这一核心素养.

例2：已知关于x的方程x2-4x+5=m有4个不等实根，试求实数m的取值范围.

分析：本题由关于x的方程开始，交代了根的个数，与方程的根的具体值毫无关联，若是直接求解，过程自然是烦琐和困难的. 经过思考，学生容易想到方程根的个数问题一般情况下可与“求两条曲线交点的个数问题”相沟通，此处以数形结合思想进行引领，体现了命题者重视数学思想对学生素养的提升.

解：方程x2-4x+5=m根的个数也就是函数y=x2-4x+5与y=m图像交点的个数.首先，作抛物线y1=x2-4x+5（x≥0）的图像;接着，作关于y轴对称的图像，即得y=x2-4x+5的图像;然后，作直线y=m（如图2所示）. 当1

评注：可以说，解决方程解的问题的方法多数都源于数形结合.首先，我们应从图形出发，借助它的直观性，巧妙作出与题意相切合的图像，从图像中找寻解题的思路，从而为此类问题的突破奠基.然后有效沟通方程和函数，结合数形结合思想展开探究，使问题的解决更简捷、更合理.

关注数形结合在复数中的应用

在探求复数问题时，若以得数及其运算的几何意义的载体去绘制图形，可使问题直观具体，从而迅速获解.数形结合思想运用于复数题，尤其是选择题和填空题中，其优越性尤为明显.

例3：设z1=5，z2=2，z1-z2=■，则■的值是__________.

分析：本题巧妙地用复数模及四则运算的几何意义通过数形结合这一载体来求解，深刻挖掘出几何图形的价值，意在关注学生数形结合的应用意识. 学生经过思考，形成以下多种解题策略：

解法1：如图3，设复数z1所对应向量为■，复数z2所对应向量为■，那么■1所对应向量为■，■2所对应向量为

据图3，可得■=■，∠AOD=∠BOC，据余弦定理，可得

cos∠AOD=■=■，

所以■=■■±■i=2±■i.

解法2：设z1=5（cosθ1+isinθ1），z2=2（cosθ2+isinθ2），

那么z1-z2=（5cosθ1-2cosθ2）+（5sinθ1+2sinθ2）i=■=■，

所以cos（θ1+θ2）=■，sin（θ1+θ2）=±■，

所以■=■=■[cos（θ1+θ2）-isin（θ1+θ2）]=■■±■i=2±■i.

评注：本题通过数形结合探究，充分展示了共轭复数的性质及复平面上的向量表示、代数运算的几何意义等，这是一种创新尝试，将数形结合的生动、形象体现得淋漓尽致. 命题者以这种智慧启迪我们，可以借助数形结合中各具特点的多种解题活动来培养学生的创新意识.

关注数形结合在解析几何中的应用

解析几何开创了数形结合的研究方法的先河，它完美展现了数形结合的优势，深刻演绎了数形结合的精髓.在解析几何的探究过程中，不仅会经历代数问题几何化的过程，还会经历几何问题代数化的过程.

例4：若实数x和y满足等式x2+y2-4x+1=0，试求出■的最大值.

分析：本题从表面材料来看，是一道关于方程和不等式的代数问题，不少学生以此思路直接求解，而求解过程甚是艰难，或者说毫无头绪. 命题者的本意为了凸显数形结合这一方法，将等式x2+y2-4x+1=0转化为（x-2）2+y2=3，由此可以自然联想到圆C，而■刚好是点（x，y）与原点连线的斜率，如此一来，问题就有了“形”. 原题可以转化为：如图4，圆C上有一动点P（x，y），试求出直线OP斜率的最大值.观察可知，点P位于第一象限，且OP与圆C相切时有PC⊥OP，则直线OP斜率最大值tan∠POC=■=■.

评注：对于题目中的表象材料，学生应当充分剖析，在夯实基本解题方法的同时掌握数学思想方法，从朴素中扎实，从创新中领悟，既需把握朴素方法，还需注重技巧化训练，让学生的解题策略在基本数学思想这一载体的渗透下，引领学生积极探究，促进“高阶”思维的培养.

总之，数形结合思想在高中数学解题中的有效渗透，可以将抽象思维洗尽铅华转化为具体的形象思维，有利于准确把握问题本质，锻炼和培养解题能力，并且获得各方面能力的提升.