高中数学教学中数学抽象再理解

刘海燕

[摘  要] 核心素养的背景下理解数学学科核心素养，只有从理论上建立起了正确的理解，那到了实践中才能符合核心素养培育的轨道. 对数学抽象的深度理解，包括这样几个方面：其一，数学抽象是发生在一定的数学情境中的;其二，数学抽象对应着复杂的思维过程，可以将这个思维过程理解为去伪存真;其三，数学抽象的过程是数学思想方法充分运用的过程.

[关键词] 高中数学;数学抽象;教学理解

自从高中数学学科核心素养正式颁布之后，其所包括的六个要素就受到高中数学教师的普遍关注，根据笔者日常教学中与同行的交流，有一个重要的发现，那就是一线教师认为这六个要素的表述都是简单易懂的，因而数学学科核心素养严格来讲并没有什么“新意”，只是对数学教学中若干个传统的融合与强调. 从概念的角度来看，这样的理解确实有一定的道理，但笔者同时又感觉这样的理解存在着一定的简单化思想. 也就是说，在核心素养的背景下理解数学学科核心素养的六个要素，应当有坚持、有创新，而且这个坚持与创新首先是理论上的坚持与创新，只有从理论上建立起了正确的理解，那到了实践中才能符合核心素养培育的轨道. 基于这样的认识，本文以数学抽象要素为例，谈谈如何深度理解数学学科核心素养.

数学抽象的基本理解与深度理解

众所周知，数学抽象是数学的基本思想，是形成理性思维的重要基础，反映了数学的本质特征，贯穿在数学产生、发展、应用的过程中. 正是数学抽象，使得数学成为高度概括、表达准确、结论一般、有序多级的系统. 这样的理解其实比较学术化，在结合教学实践的基础上，可以将这样的理解分解为基本理解和深度理解两个层次.

对数学抽象的基本理解是必要的，这是立足之基. 简单来说，数学抽象就是将形象的物体，用数学的思维去加工，仅留下与数学相关的要素，并且可以用数与形来描述. 当将“长方的物体”变成“长方形”时，将“斜抛出去的物体的运动轨迹”变成“抛物线”时……就完成了一个个数学抽象的过程. 对数学抽象建立起来的这样的基本理解，可以让教师和学生更好地步入数学抽象的大门，从而通过数学抽象去建立起数学概念或者规律，并且在数学问题解决的过程中，首先可以通过数学抽象为寻找相应的数学模型做准备.

对数学抽象的深度理解也是必要的，这是发展之基. 对数学抽象的深度理解，包括这样的几个方面：其一，数学抽象是发生在一定的数学情境中的. 当数学情境为学生提供形象、丰富的学习材料时，数学抽象才有了对象;其二，数学抽象对应着复杂的思维过程，可以将这个思维过程理解为去伪存真——所谓的伪就是与数学无关的内容，所谓的真就是与数学有关的内容;其三，数学抽象的过程是数学思想方法充分运用的过程. 数学抽象直接对应着分析与综合等基本科学方法的运用，还需要解析法、构造法等方法的参与，因此数学抽象的过程实际上也是一个培养学生运用数学思想方法的过程.

有了上述基本理解与深度理解，尤其是基本理解基础上的深度理解，那核心素养视角下数学抽象的教学，就可以从浅层走向深度，从而奠定核心素养培育的基础.

基于数学抽象深度理解实施教学

当然从行文的角度来看，本文所阐述的侧重点是数学抽象的深度理解，考虑到一线教师的需要，结合具体的案例进行分析，是实践成果得以共享的最好选择.

从一般意义的角度来看，数学抽象的落地需要在课堂教学中，让学生实质性地参与数学抽象的每一个过程，认识数学抽象这种创造性活动的一般性原则与方法. 结合上述对数学抽象深度理解的三点，这里以“函数”概念的教学为例来进行阐述.

高中阶段的函数概念，重在帮学生学习函数及其构成要素，经验表明这个过程对于相当一部分学生而言都有难度，因此教学设计的时候要尽可能地提供感性材料，以让学生进行充分的数学抽象，然后归纳得出函数的概念. 实际教学中可以提供的例子有：自由落体或者斜抛运动的实例——其中物体水平移动的距离或者竖直运动的高度，与时间之间是一对函数关系;某地区某个时间段的气温变化图，其中温度与时间之间是一对函数关系……相对而言这是学生比较熟悉的例子，可以在教学初期提供. 由于学生相对比较熟悉，所以这个时候的数学抽象往往进行得比较顺利，只要学生发现变量之间的关系即可（对于部分学困生而言，只要知道两个变量即可）.

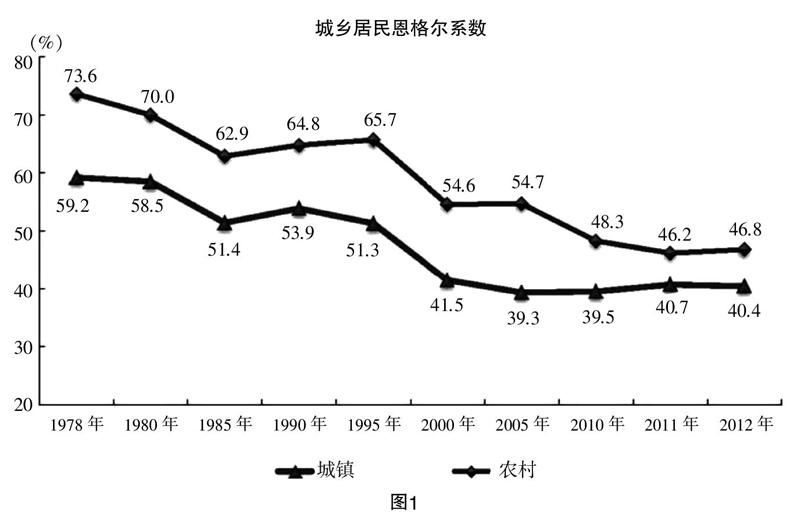
为了巩固学生数学抽象的认知，在上述两个例子的基础之上，教师可以提供一个学生相对陌生的例子来让学生分析. 这实际上是一个能力迁移的过程，对应着数学抽象深度理解中的情境提供、方法运用，以及能力迁移. 笔者在教学中举的例子是“恩格尔系数”的例子，这个素材学生相对比较陌生，但又是国民经济生活中的常用概念，客观上可以起到聯系数学与生活的作用，且可以拓宽学生的视野.

图1是1978～2012年中一些年份的恩格尔系数，观察这幅图，让学生说说自己的发现.

相比较上面的两个例子而言，这样一个图相对形象（其实本身也是抽象的产物，但是相对于表格呈现方式而言，已经比较形象了，相对于函数概念的建立而言，更是一个形象的例子，这也说明数学抽象本身是一个相对的过程），学生在利用思维进行加工的过程中，首先看到的是“趋势”，其后要努力的就是探寻恩格尔系数与年份之间的关系，而这实际上就是寻找变量的过程，也是此前形成的能力迁移到新情境中，并帮助学生完成抽象以建立函数概念的过程.

通过以上教学设计，学生在建立函数概念的过程中，多次运用到数学抽象，且会认识数学抽象得出“函数”概念的关键就是寻找变量，明确变量关系，综合、比较、概括的方法运用非常充分，是一个具有深度的数学抽象过程.

数学抽象不排斥当前评价的标准

高考是高中数学教学绕不开的话题，是当前唯一的用以评价选拔的方法. 因此，在评价标尺的背景下思考数学抽象的教学，也是务实之举.

实际上高考对数学抽象的要求历来都是有的，十多年前高考题目在抽象性方面就已经加大要求，对考生抽象概括能力提出了更高的要求，而且特别强调教师在平时的教学中必须培养学生的抽象概括能力. 即使本文提出对数学抽象应当有深度理解，其也不是以牺牲学生的考试能力为代价的，实际上数学抽象深度理解的三点内容，与高考评价是不矛盾的：分析情境进行数学抽象，是当前不少高考数学题能力立意的基础;数学思想方法的运用更体现在多种题型上;很多时候学生规避高考试题中的陷阱，实际上也是一个去伪存真的过程，从这个角度讲，数学抽象也培养了学生的应试能力，因此其与核心素养培育是两不误的. 认识到这一点，可以让数学抽象更加行稳致远！