观察联想而有深度

唐秀农

[摘  要] 深度学习和深度教学理念的引进促进高中数学教学理念、内容编排发生了变化，拓宽了学生的学习思维，丰富了教师的教学方法. 本文就深度学习和深度教学的内容选用进行分析，整合教学内容，更新了数学教学理念.

[关键词] 观察;联想;深度学习;深度教学

笔者所在学校生源位居广州市第三生源组. 学校学习风气较为浓厚，学生学习数学态度较为端正，但学生却常因自己动手解题没有思路而倍感焦头烂额，面对考试总感觉“我命由天不由我”. 经调查了解，学生普遍反映：（1）公式、定理、公理能背诵默写却不知何时何处使用;（2）看完题目无法提取有效信息;（3）能接受课堂传授知识却对课后相应练习束手无策. 笔者以为，学生存在的三个现象反映了学生在日常的学习中处于浅层学习状，尚未能对课本知识、数学思想方法进行深层次的理解与整合，未能真正意义上提高其数学核心素养. 基于以上原因，近年来，笔者在高三复习教学中尝试引导学生深度学习、进行深度教学，通过引导学生观察题目说联想和感受，主抓基础、提炼方法、重视思想的总结和提升，坚持不懈，学生的数学成绩和素养有了明显的提升.

黎加厚教授在国内首次介绍了深度学习的概念，提出深度学习是指在理解的基础上，学习者能够批判地学习新思想和事实，并将它们融入原有的认知结构中，能够在众多思想间进行联系，并能够将已有的知识迁移到新的情境中，做出决策和解决问题的学习. 具体在数学教学中的指导作用，笔者以为是学生在了解数学的定义和概念前世今生、在理解它们的内涵与外延基础上，自主提出已认知的数学知识、思想和方法，并将其和新知识内容相结合，通过对纷繁的题干观察分析、抽象联想、具体应用、回顾反思加深对知识的掌握.

习题是反映学生数学素养的镜子、是提高数学素养的桥梁. 学生通过读题、审题、联想、类比、归纳、反思，明确解题的原则，体会到学习知识从浅层次认识发端到深层次认识收尾，充分感受数学知识、思想、方法、能力、应用和技巧.

下面是“向量”一章小结复习时，由一道习题发散生成的习题课的教学实录概况.

人教版A版数学必修4第119页13题改编题：已知向量a，b满足a=b=2，a·b=2，且（a-c）·（b-2c）=0，则b-c的最小值为________.

该题初看很平常，再看似乎有些难入手，但从不同角度观察、审视、联想、剖析、探究，发现它涉及了向量的模长与数量积的运算和几何意义、点与圆的位置关系、直线与圆的位置关系、两点间的距离、点到直线的距离、三角函数的基本关系、向量三角不等式等，还涉及划归与转化、数学结合、函数等数学思想与方法，饱含丰富的知识点，具有积极的训练意义. 然而在实际教学中有些教师不屑一顾，往往就题讲题，忽视了其内在信息和引导作用，殊为可惜. 下面仅以此题为例，谈谈如何引导学生进行深入学习，以期同仁不吝指正.

对题目的外在浅层认识

认识1：见到a=b=2，a·b=2，给人的感觉是向量a，b的长度以及它们的夹角是确定不共线的，由平面向量基本定理自然想到可以将向量a，b表示向量c，那么问题就迎刃而解了.

认识2：见到已知（a-c）·（b-2c）=0，不难联想到向量数量积为零，意味着两向量互相垂直，而向量a，b的长度和夹角已经确定. 为确定向量c的位置，很快就有了对已知条件的变形（c-a）·c-■b=0，从而确定向量c的终点的轨迹是以向量a和■b终点所在线段为直径的圆.

认识3（深层）：从所求问题出发直接把求模的问题转化为求数量积也是一种常见的思路. 由（a-c）·（b-2c）=0得c2=■b·c+a·c-1，将其代入b-c2=b2-2b·c+c2，化简得b-c2=3-■b·c+a·c. 该式子中的变量既有模长，又有夹角，计算难度会增大，往下计算会导致学生半途而废或算错. 重新审视题目的条件和所求的问题，从整体上把握该式，联想到向量中的三角不等式，结合已知条件，构造一个能与条件（a-c）·（b-2c）=0有关且又能消掉向量c的式子，问题便可得解.

由所求的问题出发，通过“外在認识”将已知条件进行适当变形，寻找其几何意义，由浅到深，为即将实施的解题过程提供了夯实的条件储备——万事俱备，只欠东风.

对题目的教学分析和引导

教学分析引导1：有了认识1就知道思路之一是将向量a，b表示向量c，若是令c=xa+yb，会增加向量数量积的运算，自然而然地引导学生建立坐标系解决问题. 而在建系写点的坐标过程中，问题“求b-c的最小值”可联想到令向量b的纵坐标比令向量a为0更加容易运算，充分体现了“目标导航”的作用，减轻了计算量，体现了解题的技巧.

解法1：借助“认识1”中得到的思路，不难得到a=（1，■），b=（2，0）. 设c=（x，y），代入（a-c）·（b-2c）=0，化简得（x-1）2+y-■■=■■，即向量c的终点的轨迹是以1，■为圆心，■为半径的圆. b-c=■的几何意义为点（2，0）到圆上的点的距离，其最小值为圆心到点（2，0）的距离减去半径，即■.

“坐标法”是解与平面向量基本定理有关问题的一个通法，有助于减少运算量.

解法2：同解法1，b-c=■的几何意义是以点（2，0）为圆心的圆的半径长. 当两圆外切时，半径长最短，即圆心距离减去半径：■-■=■.

以上两种解法均为“坐标法”，此法把向量问题转化为解析几何问题，既能复习向量的知识和方法，同时又回顾了有关圆的知识，实现了一箭双雕，是解决向量问题的一种通法.

教学分析引导2：由（a-c）·（b-2c）=0可化简为（c-a）·c-■b=0，向量c的终点的轨迹是以向量a和■b的终点所在线段为直径的圆.

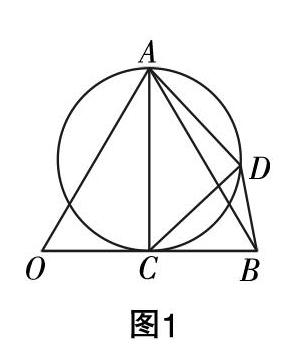
解法3：如图1所示，易得∠AOB=■，BC=1，■=■b，AC⊥OB，不妨设∠CAD=θ，则∠BCD=θ，CD=ACsinθ=■sinθ. 在△BCD中，由余弦定理得BD2=BC2+CD2-2BC·CDcosθ=1+3sin2θ-2■sinθcosθ=■-■sin（2θ+φ）tanφ=■，故BD2≥■=■=■■，当且仅当sin（2θ+φ）=1时，取到等号. 故其最小值为■.