基于核心素养下高中数学教学的情境创设

杨新鹏 董蓉艳

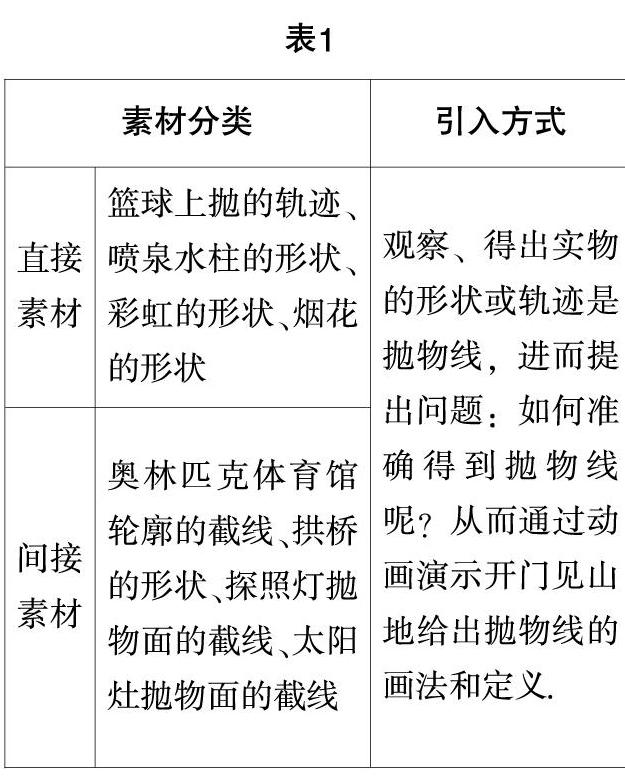
[摘  要] 学生习得的知识与学科知识的对话、互动过程，就是学生核心素养的形成过程.文章以北师大版“抛物线的定义”这一内容为例，从生活情境、操作情境、历史情境、数学情境等不同角度给出6种引入方式，以供同行参考.

[关键词] 情境;核心素养;抛物线定义

2018年11月16日，陕西师大附属中学成功举办了“全国部分大学附属中学教学协作体第二十七届年会”，此次年会的主题是“聚焦核心素养，优化课堂教学”.共有来自8所大学附属中学的32位教师进行了课堂展示，作为此次会议的参会成员，笔者有幸观摩了6位老师关于北师大版“抛物线及其标准方程第1课时”的展示课.此次展示课的一大亮点在于老师们对“抛物线的定义”一课的引入，缤彩纷呈，各具特色，都从不同角度发展了学生的核心素养.现将不同的引入方式进行整理分析，与同行交流分享.

基于生活情境

抛物线的模型在生活中随处可见，所以通过实物模型引入抛物线是一种简单、直接的方式，此次展示课中，6位老师中有2位采用了通过创设生活情境引入抛物线，以下是他们使用的素材和引入方式（见表1）.

分析：从学生已有的经验出发，开门见山，创设与生活密切相关的情境，把生活经验数学化，数学问题生活化，不仅体现了数学源于生活的理念，也有利于吸引学生的注意力，激发学生的学习兴趣，发展学生数学抽象、直观想象的能力.

基于操作情境

所谓操作情境，就是指根据学生所要学习的数学知识或所要解决的数学问题的特点设计需要学生自己主动参与的操作性活动.

情境创设

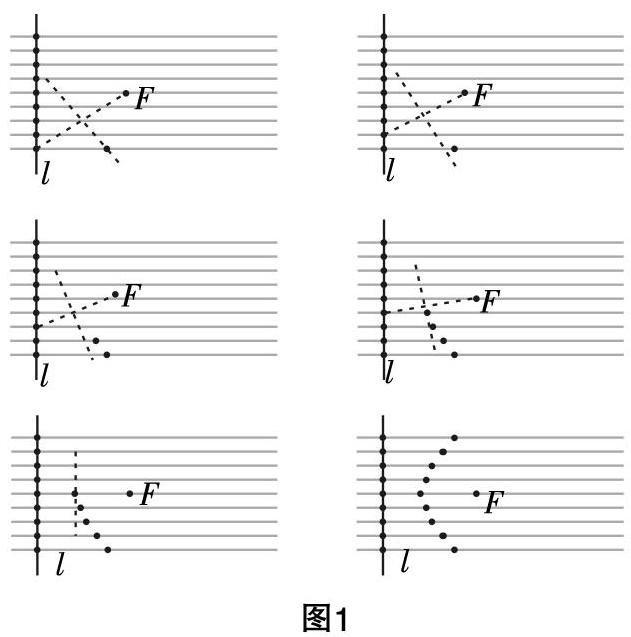
师：如图1，选择一张画有等距平行格线的纸张，作一条垂直格线的直线l，直线l与格线相交于9个空心点，在纸张中心位置取一定点F，依次连接空心点与定点F，再分别作连线的垂直平分线，依次交平行格线得到9个交点. 再用平滑的曲线连接每个交点，并思考由对折形成的交点满足什么样的几何条件？

学生：动手操作，用平滑的曲线依次连接每个交点，得到一条抛物线.

师：得到的每个交点与定点F和定直线l有何关系？

学生：每个交点到定点F和到定直线l的距离相等.

师：同学们可以对抛物线下一个定义吗？

分析：学生对抛物线定义的提炼及理解是本节课的一个重点，设计一个折纸试验，能够让学生在动手操作的过程中，经历抛物线的形成过程，从而对定义有更深刻的理解.通过试验来归纳、抽象出抛物线的定义，有助于发展学生逻辑推理、数学抽象的核心素养.

生活情境与操作情境相结合

情境创设

问题1：某村庄有两处水源：一条河和一口井，请你画一条合理的取水分界线，供村民取水时参考.

问题2：实际问题中涉及哪些实物？又该把它们抽象成什么数学对象呢？

学生：河、井，河可以抽象成一条直线，井可以抽象成一个定点，村民的家抽象成平面内的一些点.

问题3：分界线上的点满足怎样的几何条件呢？

学生：分界线上的点到定点距离等于到定直线的距离.

問题4：请同学描出满足要求的几个点，并将点连接成线，了解曲线的大致形状.

学生：通过直观感觉描出3个点，大致看出3个点的连线接近于抛物线形状.

师：通过动画演示增加点的个数，随着点数的增加，取水分界线越来越接近于一条开口向上的抛物线，从而引导学生归纳出抛物线的定义和推导出开口向上的抛物线的方程.

分析：画出取水分界线，为学生提供一个能够探究问题的情景，而不是提供现成的知识.根据实际问题的特点，将实际问题转化为几何问题，有助于提升学生数学抽象的核心素养.通过模拟实际问题的背景，学生对形成的几何图形有了直观的感知，并归纳得出分界线上点的几何性质，有利于培养学生的观察能力、分析能力和归纳能力.

基于历史情境

历史情境是以数学的历史发展为出发点，教师通过对历史的解读和理解，选择具有科学性的、针对性的、趣味性的数学史知识进行引入，让学生了解数学知识的发现过程，学习数学家探索和发现数学知识的思想与方法，实现对数学知识的再发现过程.

情境创设

希腊数学家阿波罗尼奥斯在其著作《圆锥曲线》中用一个与圆锥的一条母线平行的平面去截该圆锥，他把该平面与该圆锥截得的交线命名为抛物线，那么这条抛物线有什么特点？

师：如图4所示，一个圆锥里面放置一个球体，一个与母线CE平行且与球体相切的平面MAPG去截圆锥，截出的交线是一条抛物线.BC与球O相切，将BC平移可以得到DO，DO平移得到PA，易证OD⊥AM，所以PA⊥AM.又PQ与PF都与球相切，所以PQ=PF，而PQ=BC，所以PF=BC=PA，所以点P到定直线AM与到定点F的距离相等，点P为截面与上底面圆环的交点，这样的交点都在抛物线上，它们都满足到定直线AM与到定点F的距离相等.

分析：基于历史的情境创设方式，揭示了抛物线概念的形成过程，不仅增强课堂的趣味性和文化性，而且使学生对概念有更加深入的理解，提高学生对知识的迁移能力，发展学生逻辑推理和数学抽象的核心素养.需要说明的是，整个引入对历史事实的解释和证明难度较大，学生难以在较短的时间内接受.所以只需要进行简单的史实介绍，让学生了解就行.

基于数学情境

从数学知识的产生过程来看，数学的初次抽象建立在以现实生活情境为素材的原型之上;数学一经构造就具有“形式客观性”和“相对独立性”，从而又可以成为进一步抽象的“具体原型”.因此，数学情境也可以源于数学自身.

情境创设1

1. 给出两个数学问题：

（1）已知动点P到定点F（0，1）的距离与到直线y=-1的距离相等，则点P的轨迹是什么？

学生：通过计算得到点P的轨迹方程为y=■x2，为开口向上的抛物线.

（2）已知动点P到定点F（1，0）的距离与到直线x=-1的距离相等，则点P的轨迹是什么？

学生：通过计算得到点P的轨迹方程为y2=4x，猜测为开口向右的抛物线.

2. 利用图形计算器画出上述两个问题中动点的轨迹，观察第二个图像是不是抛物线？两个图像有什么关系？

学生：运用图形计算器，发现第二个图像仍为抛物线，并且两个图像关于y=x对称.

3. 请问这两个问题中点P的条件有什么共性？

学生：点P到定点距离等于到定直线的距离.

师：你能给抛物线下一个定义吗？（给出抛物线的定义）

情境创设2

师： 在抛物线y=■x2上任取几个点，计算这几个点到定点（0，1）和到定直线y=-1的距离，观察结果，得到什么结论？

学生：通过计算发现，抛物线y=■x2上任意选取的点到定点（0，1）和到定直线y=-1的距离相等.可设抛物线y=■x2上的点为a，■a2，易得a，■a2到（0，1）的距离为■= ■=■a2+1，a，■a2到y=-1的距离为■a2+1=■a2+1，所以抛物线y=■x2上的每个点到定点（0，1）和到定直线y=-1的距离都相等.

师：看来，平面内给定一条抛物线，存在一个定点和一条定直线，使得抛物线上的点到这个定点和这条定直线的距离相等.那么反之，平面内到一个定点和一条定直线的距离相等的点的轨迹是抛物线吗？（引导学生推导抛物线的标准方程）

分析：以上两种方式，都是以数学问题为载体，从二次函数图像是抛物线这个认知基础出发，引发学生对抛物线进行更深层次的思考. 第一种方式中，学生可在实践操作中，体会抛物线几何本质发挥的作用，在此基础上，提炼概念，补充概念，运用概念.第二种方式探究抛物线上的几个特殊点到定点和定直线距离的关系，进而探究抛物线上任意一点到定点和定直线的距离关系，发现规律，从特殊到一般，反过来，研究满足到定点和定直线距离相等的点的轨迹是否是抛物线，体现了曲线与方程的纯粹性和完备性，两种方式都不同程度地发展了学生数学抽象和逻辑推理能力。