一堂数学“母题”变式教学课的实录与感悟

王敏

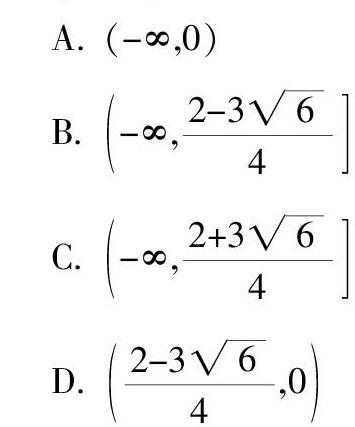
[摘  要] 通过一堂导数与不等式的“母题”变式教学课的呈现，谈几点感悟，认为：“母题”变式教学体现了教师的主导作用和学生的主体地位，通过控制题量，有效实现了课堂教学减负，把学生的思维水平提高了一个层次.

[关键词] 母题;变式;实录;感悟

高考复习，从某个角度看，就是高考题型的研究和高考实战演习. 如何研究题型，让学生的实战演习更有效. 笔者以为，“母题”变式研究与训练，是一个不错的选择. 所谓“母题”变式，就是把一个典型例题作为“母题”，教师引导学生对其深入研究，并产生与之相关的系列题型，再让学生训练，这种从一道题引发数学研究的教学模式，不仅能让学生“跳出题海”，更能让学生感受自己编题（找题）自己做的乐趣[1]. 下文是笔者一堂导数与不等式的“母题”变式教学课的实录与感悟，供大家参考.

教学实录

1. 出示“母题”，引出复习课题

母题：（2018-2019学年湖北省黄冈中学、华师附中等八校联考）已知函数h（x）=alnx+（a+1）x2+1（a<0），在函数h（x）图像上任取两点A，B，若直线AB的斜率的绝对值都不小于5，则实数a的取值范围是（  ）

A. （-∞，0）

B. -∞，■

C. -∞，■

D. ■，0

教师提出问题：

问题1：这道题主要研究什么？

生1：利用导数研究不等式问题.

问题2：如何解这道题？即这道题的解题思路是什么？

生2：先对函数求导，将已知“直线AB的斜率的绝对值都不小于5”，去绝对值.然后构造函数f（x）=h（x）+5x，利用导数求得函数f（x）的单调区间，利用一元二次不等式恒成立问题的解法，求得a的取值范围.

问题3：这道题主要考查什么？即考点是什么？

生3：本题考查利用导数的工具性研究不等式恒成立问题.

教师请学生根据刚才的分析自行完成，并展示. （这里略，答案：B）

教師出示本节课复习的主题：导数与不等式问题.

说明：教师对“母题”的选择必须具有新颖性、代表性，且紧扣考纲与考点.

2. 集思广益，总结子题题型

师：刚才的一道“母题”，体现了导数在不等式问题中的应用. 那么，利用导数能解决哪些不等式问题呢？请以小组为单位，加以探讨，5分钟后交流.

学生分组讨论，教师巡视. 5分钟后请以小组委派一名学生交流.

小组1：利用导数比较数值大小.

小组2：利用导数解不等式.

小组3：利用导数解决不等式恒成立问题.

小组4：利用导数证明不等式.

教师点评：同学们刚才集思广益后提出的四种问题，的确是导数与不等式的最常见的四种题型. 在高考真题和各地的模拟卷中，这四类问题频频出现，主要考查考生对导数的灵活应用，我们不仅要把握基本题型，更要把握具体的解题方法.

？摇3. 分组组题，展示资料共享

师：有道是“是牛是马，牵出来遛遛”. 空口无凭，有例才为证. 请同学们，继续以小组为单位，找出与本组提出题型有关的题目2至3个.

教师继续巡视，及时回答学生组题时遇到的问题或疑惑. 20分钟后仍以小组为单位委派一名学生进行交流.

小组1：刚才我们小组归纳的题型是利用导数比较数值大小，请看下面的3个题：？摇？摇？摇？摇？摇？摇？摇？摇？摇？摇

（1）已知函数f（x）=■，则f（2），f（e），f（3）的大小关系是______.

（2）函数f（x）在定义域R内可导，若f（1+x）=f（3-x），且当x∈（-∞，2）时，（x-2）f′（x）<0，设a=f（0），b=f■，c=f（3），则a，b，c的大小关系是______.

（3）f（x）是定义在非零实数集上的函数，f′（x）为其导函数，且x>0时，xf′（x）-f（x）<0，记a=■，b=■，c=■，则a，b，c的大小关系是______.

？摇 小组2：刚才我们小组归纳的题型是利用导数解不等式，请看下面的3个题：

（1）已知函数f′（x）是函数f（x）的导函数，f（1）=■，对任意实数都有f（x）-f′（x）>0，则不等式f（x）

（2）定义域为R的可导函数y=f（x）的导函数为f′（x），满足f（x）>f′（x），且f（0）=1，则不等式■<1的解集为________.

（3）定义在（0，+∞）上的函数f（x）满足x2f′（x）+1>0，f（1）=6，则不等式f（lgx）< ■+5的解集为________.

小组3：刚才我们小组归纳的题型是导数与不等式恒成立问题，请看下面的3个题：

（1）已知函数f（x）=ax3-3x+1对x∈（0，1]总有f（x）≥0成立，则实数a的取值范围是________.

（2）已知a，b∈R，直线y=ax+b+■与函数f（x）=tanx的图像在x=-■处相切，设g（x）=ex+bx2+a，若在区间[1，2]上，不等式m≤g（x）≤m2-2恒成立，则实数m有________.

？摇（3）设函数f（x）在R上存在导函数f′（x），对任意的实数x都有f（x）=4x2-f（-x），当x∈（-∞，0）时，f′（x）+■<4x. 若f（m+1）≤f（-m）+3m+■，则实数m的取值范围是________.

小组4：刚才我们小组归纳的题型是导数与不等式的证明，我们找到了下面两道题，供同学们参考：

（1）已知x=1为函数g（x）=x（lnx-c）的极值点. 证明：当x>1时，g（x）

（2）已知函数f（x）=■-lnx. ①求f（x）的单调区间;②求证：ln■≤■.

4. 点拨思路，学生独立完成

师：同学们组的题目都紧扣题型，十分精彩，我发现有些题目还是最新出现的模考题，这说明我们同学身边的资料真的不少，开卷有益，它山之石，可以攻玉，这很好！同学们找题的目的是为了解题，那么这类问题该如何解答？利用导数解决不等式问题，归根到底是利用导数研究函数的单调性，进而再利用函数的单调性解决问题[2]. 因此，解决这些问题，一般都要构造函数，本质上看，这类问题考查的还是导数与函数的关系.

师：好，今天的作业就是请大家完成刚才大家组的11个有关导数与不等式的题目，请注意：原则上独立完成，若确有困难，则允许合作讨论.

三点感悟

感悟1：數学习题课一般都是由教师提供题目，学生练习题目，学生只顾埋头做题，往往不知题从何来，不知题目所涉及的考点，这样的练习往往缺乏对题目的研究，是一种为解题而解题的复习模式，学生不能对题目产生理性的认识. 而从教师提供的“母题”出发，让学生自己去找题，要完成这个任务，学生务必明确题型，否则很难“对号入座”，于是将学生的“解题”转化为“题解”，从而把学生的思维水平提高了一个层次.

感悟2：减负，是当今中小学教育界沉重的话题. 如何将学生从沉重的课业中解放出来，让他们“跳出题海”，是每位教师关心的问题[3]. 而“母题”变式教学模式，从很大程度上控制了题量，并允许合作完成，从而让他们练有所获，练有所成. 与此同时，也减轻了教师的负担，让学生自行找题，有时会更切合实际，比教师找题更有效. 自己选的题目自己做，这更能提高学生训练的积极性.

感悟3：任何一堂课都应该体现教师的主导作用和学生的主体地位. 教师一讲到底，这种“填鸭式”的教学模式完全削弱了学生的主体地位，早已被大家摒弃. 而“母题”变式教学模式，教师俨然是教学的组织者和指导者，而不是“主宰”，探讨的问题虽然由教师引发，但问题的进展由学生决定，这种把学习的主动权交还给学生的教学模式，能使课堂气氛和谐，师生关系融洽，从而能达到较好的教学效果.

参考文献：

[1]  江卫军. 高中函数母题研究[D].苏州大学，2016.

[2]  赵子兵. 利用导数处理与不等式有关的问题[J]. 中学数学研究，2011（12）.

[3]  范爽. 关于“课业负担”的若干基本理论问题研究[D]. 沈阳师范大学，2013.